Применение дифференциальных уравнений в задачах экономики

Дифференциальные уравне­ния находят достаточно широкое применение в моделях экономической дина­мики, в которых отражается не только зависимость переменных от времени, но и их взаимосвязь во времени.

Рассмотрим некоторые простейшие задачи макроэкономической динамики.

Задача 1. Пусть y=y(t) – объем продукции некоторой отрасли, реализованной к моменту времени t. Предположим, что цена на дан­ный товар остается постоянной (в пределах рассматриваемого про­межутка времени). Тогда функция y=y(t) удовлетворяет уравнению

, (20)

где 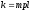, m – норма инвестиций, p – продажная цена, l – коэф­фициент пропорциональности между величиной инвестиций и скоро­стью выпуска продукции.

Уравнение (20) является уравнением с разделяющимися перемен­ными. Его решение имеет вид

,

где .

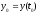Предположение о неизменности цены (о ненасыщаемости рын­ка) на практике оказывается справедливым лишь для узких вре­мен­ных интервалов.

В общем случае цена р является убывающей функцией от объема у реализованной продукции 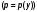. Тогда уравнение (20) прини­мает вид

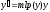. (21)

Это уравнение является тоже уравнением с разделяющимися перемен­ными.

Замечнание. Уравнение (20) описывает также рост народонаселения, динамику роста цен при постоянной инфляции, процесс радиоктивного распада и  др. Уравнение вида (21) описывает рост народонаселения при наличии (естественных) ограничений для этого роста, динамику разви­тия эпидемий, процесс распространения рекламы и т. д.

Задача 2. Доход Y(t), полученный к моменту времени t некоторой отраслью, является суммой инвестиций I(t) и величины потребления С(t), т. е.

. (22)

Будем предполагать, что скорость увеличения дохода пропорциональна величине инвестиций, т. е.

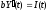, (23)

где b – коэффициент капиталоемкости прироста дохода.

Рассмотрим поведение функции дохода Y(t) в зависимости от функции С(t).

Пусть С(t) представляет фиксированную часть получаемого дохода: 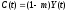, где m – норма инвестиций. Тогда из уравнений (22) и (23) получаем

,

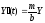Что равносильно уравнению (20) при p=const.

В ряде случаев вид функции потребления С(t) бывает известен (из некоторых дополнительных соображений).

Числовые и функциональные ряды План

Числовые ряды, основные понятия. Свойства сходящихся рядов. Необходимый признак сходимости ряда. Достаточные признаки сходимости числовых рядов с положительными членами. Знакопеременные ряды. Абсолютная и условная сходимость.

Функциональные ряды, основные понятия. Степенные ряды и методы нахождения области сходимости. Ряды Тейлора и Маклорена.

Основные понятия. Сходимость ряда

Определение 1. Числовым рядом называется бесконечная последовательность чисел 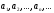соединенных знаком сложения:

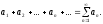(1)

Числа называются членами ряда, а член 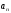– общим или n-м членом ряда.

Ряд (1) считается заданным, если известен его общий член , т.е. задана функция f(n) натурального аргумента.

Рассмотрим суммы конечного числа членов ряда:

Сумма n первых членов ряда называется n-й частичной суммой ряда.

Определение 2. Ряд называется сходящимся, если существует конечный предел последовательности 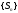его частичных сумм, т. е.

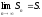(2)

Число S называется суммой ряда.

Если же 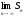не существует или 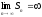, то числовой ряд называется расходящимся. Такой ряд суммы не имеет.

Свойства рядов

1. Если ряд 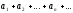сходится и имеет сумму S, то и ряд (полученный умножением каждого его члена на число ) также сходится и имеет сумму .

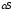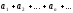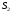2. Если ряды и сходятся и их суммы соответственно равны и , то и ряд (представляющий сумму данных рядов) также сходится, и его сумма равна .

3. Если ряд сходится (расходится), то сходится (расходится) и ряд, полученный из данного путем отбрасывания любого конечного числа его членов.

Определение 3. Ряд

, (3)

полученный из ряда (1) отбрасыванием его первых n членов, называется n-м остатком ряда.

Ряд (1) получается из остатка (3) добавлением конечного числа членов. Поэтому, согласно свойству (3), ряд (1) и его остаток (3) сходятся и расходятся одновременно.

Из свойства (3) также следует, что если ряд (1) сходится, то его остаток стремится к нулю при , т. е. .
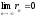