Основные свойства неопределенного интеграла

Рассмотрим свойства неопределенного интеграла, вытекающие из его определения.

1. Производная от неопределенного интеграла равна подынтегральной функции, дифференциал от неопределенного интеграла равен подынтегральному выражению:

Доказательство.

Пусть Тогда

и

2. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной:

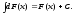
Доказательство.

Действительно, .

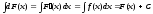3. Постоянный множитель a () можно выносить за знак неопределенного интеграла:

4. Неопределенный интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме интегралов от этих функций:

5. Если F(x) – первообразной функции f(x), то

Доказательство.

Действительно,

6 (инвариантность формул интегрирования). Любая формула интегрирования сохраняет свой вид, если переменную интегрирования заменить любой дифференцируемой функцией этой переменной:

где u – дифференцируемая функция.

Таблица основных неопределенных интегралов

Так как интегрирование есть действие, обратное дифференцированию, то большинство из приводимых формул может быть получено обращением соответствующих формул дифференцирования. Другими словами, таблица основных формул интегрирования получается из таблицы производных элементарных функций при обратном ее чтении (справа налево).

Приведем таблицу основных неопределенных интегралов. (Отметим, что здесь, как и в дифференциальном исчислении, буква u может означать как независимую переменную (u=x), так и функцию от независимой переменной (u=u(x)).)

1		7
2		8
3		9
4		10
5		11
6		12

Интегралы 1–12 называются табличными.

Некоторые из приведенных выше формул таблицы интегралов, не имеющие аналога в таблице производных, проверяются дифференцированием их правых частей.

Основные методы интегрирования

Непосредственное интегрирование. Вычисление интегралов, основанное на приведении подынтегрального выражения к табличной форме и использовании свойств неопределенного интеграла, называется непосредственным интегрированием.

При сведении данного интеграла к табличному часто используются следующие преобразования дифференциала (операция «подведения под знак дифференциала»):

1.

2.

3.

Интегрирование подстановкой (заменой переменной). Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (т.е. подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся.

Пусть требуется вычислить интеграл , который не является табличным. Сделаем подстановку 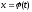, откуда 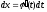На основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой:

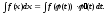(2)

Формула (2) также называется формулой замены переменных в неопределенном интеграле. После нахождения интеграла в правой части этого равенства следует перейти от новой переменной интегрирования t назад к переменной x.

Иногда целесообразно выбирать подстановку , тогда

Другими словами, формулу (2) можно применять справа налево.

Интегрирование по частям.

Пусть u=u(x) и v=v(x) – функции, имеющие непрерывные производные. Тогда Интегрируя это равенство, получим

или

(3)

Полученная формула называется формулой интегрирования по частям. Она дает возможность свести вычисление интеграла 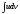к вычислению интеграла , который может оказаться более простым, чем исходный.

Укажем некоторые типы интегралов, которые удобно вычислять методом интегрирования по частям.

1. Интегралы вида , где – многочлен степени n, а k – некоторое число. Чтобы найти эти интегралы, достаточно положить и применить формулу (3) n раз.

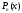2. Интегралы вида где – многочлен степени n. Чтобы найти эти интегралы, нужно применить формулу (3), принимая за u функцию, являющуюся множителем при .

3. Интегралы вида (a, b – числа). Они вычисляются двукратным интегрированием по частям.