
- •GfВведение в математический анализ План
- •Множества
- •Операции над множествами
- •Понятие функции, ее области определения и множества значений. Способы задания функции
- •Основные свойства функции
- •Понятие обратной функции
- •Понятие сложной функции
- •Применение функций в экономике
- •Числовые последовательности
- •Предел последовательности
- •Число е, применение в экономике
- •Предел функции
- •Замечательные пределы
- •Бесконечно малые, бесконечно большие функции
- •Классификация бесконечно малых
- •Односторонние пределы функции
- •Непрерывность функции, классификация точек разрыва
- •Основы дифференциального исчисления функции одной переменной План
- •Определение производной
- •Геометрический и физический смысл производной
- •Связь между непрерывностью и дифференцируемостью функции
- •Правила дифференцирования функций
- •Дифференцирование сложной, обратной функций
- •Производная неявной и параметрически заданной функций
- •Определение и геометрический смысл дифференциала
- •Производные высших порядков явно заданной функции
- •Производные высших порядков неявно заданной функции
- •Производные высших порядков параметрически заданной функции
- •Дифференциалы высших порядков
- •Основные теоремы дифференциального исчисления
- •Раскрытие неопределенностей с помощью правила Лопиталя
- •Формула Тейлора
- •Разложение по формуле Маклорена некоторых элементарных функций
- •Исследование функций с помощью производных Условия возрастания и убывания функции
- •Понятие экстремума
- •Выпуклость графика функции. Точки перегиба
- •Асимптоты графика функции
- •Применение производных в экономике
- •Функция нескольких переменных План
- •Определение функции нескольких переменных. Область определения
- •Линии уровня
- •Предел функции нескольких переменных
- •Непрерывность функции нескольких переменных
- •Частные производные первого и высших порядков
- •Полный дифференциал и его применение при приближенных вычислениях
- •Дифференциалы высших порядков
- •Производная по направлению, градиент функции
- •Экстремум функции нескольких переменных
- •Наибольшее и наименьшее значения функции нескольких переменных в замкнутой области
- •Условный экстремум. Метод множителей Лагранжа
- •Метод наименьших квадратов
- •Основы интегрального исчисления План
- •Первообразная функции и неопределенный интеграл
- •Основные свойства неопределенного интеграла
- •Основные методы интегрирования
- •Рациональные дроби
- •Интегрирование простейших рациональных дробей
- •Интегрирование рациональных дробей
- •Интегрирование тригонометрический функций
- •Интегрирование некоторых иррациональных функций
- •Интегралы, не выражающиеся через элементарные функции
- •Определенный интеграл
- •Основные свойства определенного интеграла
- •Определенный интеграл с переменным верхним пределом
- •Формула Ньютона – Лейбница
- •Основные методы вычисления определенного интеграла
- •Геометрические приложения определенного интеграла
- •Некоторые приложения определенного интеграла в экономике
- •Несобственные интегралы
- •Дифференциальные уравнения План
- •Общие сведения о дифференциальных уравнениях
- •Дифференциальные уравнения первого порядка (общие понятия)
- •Уравнения с разделяющимися переменными
- •Однородные дифференциальные уравнения
- •Линейные уравнения. Уравнения я. Бернулли
- •Дифференциальные уравнения второго порядка (основные понятия)
- •Уравнения, допускающие понижение порядка
- •Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Линейные однородные уравнения второго порядка
- •Неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Применение дифференциальных уравнений в задачах экономики
- •Числовые и функциональные ряды План
- •Основные понятия. Сходимость ряда
- •Необходимый признак сходимости
- •Достаточные признаки сходимости рядов с положительными членами
- •Знакочередующиеся ряды. Признак Лейбница
- •Знакопеременные ряды. Общий достаточный признак сходимости знакопеременных рядов
- •Функциональные ряды. Степенные ряды. Сходимость степенных рядов
- •Ряды Тейлора и Маклорена
Определение производной
Пусть
функция
у = f(x)
определена в некоторой окрестности
точки
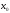 .
Если
фиксированное значение аргумента
.
Если
фиксированное значение аргумента
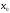 получает приращение
получает приращение
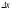 (положительное
или отрицательное, и
(положительное
или отрицательное, и
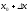 также принадлежит окрестности точки
также принадлежит окрестности точки
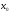 ),
то приращение функции определяется
выражением
),
то приращение функции определяется
выражением
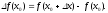
Определение
1.
Производной
функции у = f(x)
в
произвольной фиксированной точке
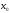 называется предел (если он существует
и конечен) отношения приращения функции
к приращению
аргумента, когда приращение аргумента
стремится к нулю.
называется предел (если он существует
и конечен) отношения приращения функции
к приращению
аргумента, когда приращение аргумента
стремится к нулю.
Производная
функции у = f(x)
в точке
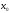 обозначается:
обозначается:
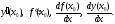
Таким образом,
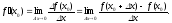 (1)
(1)
Производная
функции у = f(x)
в
произвольной точке x
обозначается:
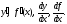
При
каждом конкретном числовом значении x
производная функции у = f(x)
(если
она существует при данном x)
есть некоторое число. Значениям
переменной x
ставятся в соответствие определенные
значения переменной
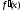 .
Следовательно, производная данной
функции есть некоторая функция аргумента
x.
.
Следовательно, производная данной
функции есть некоторая функция аргумента
x.
Функция, имеющая конечную производную, называется дифференцируемой. Операция нахождения производной называется дифференцированием.
Геометрический и физический смысл производной
Геометрический
смысл производной.
Производная от функции у = f(x)
при
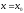 равна
угловому коэффициенту (тангенсу угла
наклона) касательной, проведенной к
графику этой функции в точке
с
абсциссой
равна
угловому коэффициенту (тангенсу угла
наклона) касательной, проведенной к
графику этой функции в точке
с
абсциссой
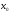 ,
т. е.
,
т. е.
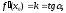 (2)
(2)
где
 угол
между касательной к графику функции
у = f(x)
в
точке
угол
между касательной к графику функции
у = f(x)
в
точке
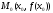 и положительным направлением оси Ох.
и положительным направлением оси Ох.
Физический
смысл производной.
Для функции у = f(x),
определенной и непрерывной в точке
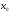 ,
отношение
,
отношение
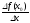 есть средняя скорость изменения функции
за промежуток
есть средняя скорость изменения функции
за промежуток
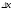 ,
а
,
а
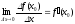 есть мгновенная скорость ее изменения
в точке
есть мгновенная скорость ее изменения
в точке
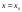 .
.
Таким образом, производная от функции у = f(x) – математическая модель мгновенной скорости процесса, описываемого данной функцией. В зависимости от содержания можно получить различные математические модели скорости протекания физических, химических и других процессов.
Например,
пусть материальная точка М
движется неравномерно и у = s(t)
– функция, устанавливающая зависимость
пути от времени t.
Тогда мгновенная скорость v
движения в момент времени
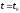 есть производная от пути s
по
времени t:
есть производная от пути s
по
времени t:
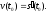
Рассмотрим
еще один пример. Пусть u=u(t)
функция, которая выражает количество
произведенной
продукции u
за время t.
Отношение
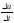 есть средняя производительность труда
за период времени
есть средняя производительность труда
за период времени
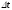 .
Тогда производительность труда z
в момент времени
.
Тогда производительность труда z
в момент времени
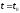 есть производная объема произведенной
продукции u
по
времени t:
есть производная объема произведенной
продукции u
по
времени t:
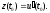
Последний пример иллюстрирует экономический смысл производной.
Связь между непрерывностью и дифференцируемостью функции
Теорема
1
(о
непрерывности функции в точке).
Если
функция у = f(x)
имеет конечную производную в точке
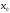 ,
то она непрерывна в этой точке.
,
то она непрерывна в этой точке.
Обратное
утверждение не всегда верно: если функция
у = f(x)
непрерывна в некоторой точке
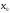 ,
она может и не иметь производной в этой
точке.
,
она может и не иметь производной в этой
точке.
Например,
функция
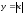 определена и непрерывна во всех точках
x
числовой оси R,
однако в точке
определена и непрерывна во всех точках
x
числовой оси R,
однако в точке
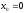 не имеет производной.
не имеет производной.
Замечание. Производная непрерывной функции не обязательно непрерывна.
