
- •GfВведение в математический анализ План
- •Множества
- •Операции над множествами
- •Понятие функции, ее области определения и множества значений. Способы задания функции
- •Основные свойства функции
- •Понятие обратной функции
- •Понятие сложной функции
- •Применение функций в экономике
- •Числовые последовательности
- •Предел последовательности
- •Число е, применение в экономике
- •Предел функции
- •Замечательные пределы
- •Бесконечно малые, бесконечно большие функции
- •Классификация бесконечно малых
- •Односторонние пределы функции
- •Непрерывность функции, классификация точек разрыва
- •Основы дифференциального исчисления функции одной переменной План
- •Определение производной
- •Геометрический и физический смысл производной
- •Связь между непрерывностью и дифференцируемостью функции
- •Правила дифференцирования функций
- •Дифференцирование сложной, обратной функций
- •Производная неявной и параметрически заданной функций
- •Определение и геометрический смысл дифференциала
- •Производные высших порядков явно заданной функции
- •Производные высших порядков неявно заданной функции
- •Производные высших порядков параметрически заданной функции
- •Дифференциалы высших порядков
- •Основные теоремы дифференциального исчисления
- •Раскрытие неопределенностей с помощью правила Лопиталя
- •Формула Тейлора
- •Разложение по формуле Маклорена некоторых элементарных функций
- •Исследование функций с помощью производных Условия возрастания и убывания функции
- •Понятие экстремума
- •Выпуклость графика функции. Точки перегиба
- •Асимптоты графика функции
- •Применение производных в экономике
- •Функция нескольких переменных План
- •Определение функции нескольких переменных. Область определения
- •Линии уровня
- •Предел функции нескольких переменных
- •Непрерывность функции нескольких переменных
- •Частные производные первого и высших порядков
- •Полный дифференциал и его применение при приближенных вычислениях
- •Дифференциалы высших порядков
- •Производная по направлению, градиент функции
- •Экстремум функции нескольких переменных
- •Наибольшее и наименьшее значения функции нескольких переменных в замкнутой области
- •Условный экстремум. Метод множителей Лагранжа
- •Метод наименьших квадратов
- •Основы интегрального исчисления План
- •Первообразная функции и неопределенный интеграл
- •Основные свойства неопределенного интеграла
- •Основные методы интегрирования
- •Рациональные дроби
- •Интегрирование простейших рациональных дробей
- •Интегрирование рациональных дробей
- •Интегрирование тригонометрический функций
- •Интегрирование некоторых иррациональных функций
- •Интегралы, не выражающиеся через элементарные функции
- •Определенный интеграл
- •Основные свойства определенного интеграла
- •Определенный интеграл с переменным верхним пределом
- •Формула Ньютона – Лейбница
- •Основные методы вычисления определенного интеграла
- •Геометрические приложения определенного интеграла
- •Некоторые приложения определенного интеграла в экономике
- •Несобственные интегралы
- •Дифференциальные уравнения План
- •Общие сведения о дифференциальных уравнениях
- •Дифференциальные уравнения первого порядка (общие понятия)
- •Уравнения с разделяющимися переменными
- •Однородные дифференциальные уравнения
- •Линейные уравнения. Уравнения я. Бернулли
- •Дифференциальные уравнения второго порядка (основные понятия)
- •Уравнения, допускающие понижение порядка
- •Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Линейные однородные уравнения второго порядка
- •Неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Применение дифференциальных уравнений в задачах экономики
- •Числовые и функциональные ряды План
- •Основные понятия. Сходимость ряда
- •Необходимый признак сходимости
- •Достаточные признаки сходимости рядов с положительными членами
- •Знакочередующиеся ряды. Признак Лейбница
- •Знакопеременные ряды. Общий достаточный признак сходимости знакопеременных рядов
- •Функциональные ряды. Степенные ряды. Сходимость степенных рядов
- •Ряды Тейлора и Маклорена
Число е, применение в экономике
Определение
17.
Числом е
(число Эйлера) называется предел
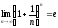 ,
где
,
где
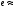 2,71828…
– иррациональное число.
2,71828…
– иррациональное число.
К использованию числа e приводит анализ таких процессов, как рост народонаселения, распад радия, размножение бактерий и так далее. Число e используется так же при решении экономических задач.
Процентом
P
называется сумма, выплачиваемая за
использование предоставленных средств
 .
Тогда величина
.
Тогда величина
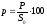 ,
выраженная в процентах, называется
процентной
ставкой.
По истечению установленного срока
накопленная сумма составит:
,
выраженная в процентах, называется
процентной
ставкой.
По истечению установленного срока
накопленная сумма составит:
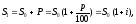
где
 называется удельной
процентной ставкой.
Если в дальнейшем на накопленную сумму
процент не начисляется, то процент
называется простым,
а накопленная сумма через n
лет составит
называется удельной
процентной ставкой.
Если в дальнейшем на накопленную сумму
процент не начисляется, то процент
называется простым,
а накопленная сумма через n
лет составит
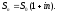
Процент
называется сложным,
если на очередной период процент
начисляется на всю накопленную сумму
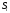 .
В этом случае, накопленная за Т
лет сумма
.
В этом случае, накопленная за Т
лет сумма
 ,
определяется по формуле
,
определяется по формуле

Рассмотрим задачу о непрерывном начислении процентов.
Задача.
Пусть вклад
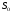 денежных
единиц положен в банк под p
процентов годовых. Найти размер вклада
через Т
лет при условии, что начисление процентов
производится n
раз в год.
денежных
единиц положен в банк под p
процентов годовых. Найти размер вклада
через Т
лет при условии, что начисление процентов
производится n
раз в год.
Решение. В результате одноразового начисления процентов величина вклада станет равной
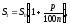
где
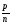 –
процент начисления за
–
процент начисления за
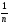 часть года.
часть года.
За год проценты на вклад будут начислены n раз. Воспользовавшись формулой сложных процентов, получим величину вклада через год:

Через T лет величина вклада окажется равной
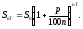
Предположив,
что
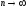 ,
получим величину вклада при непрерывном
начислении процентов:
,
получим величину вклада при непрерывном
начислении процентов:

Зависимость величины вклада от времени имеет экспоненциальный характер.
Формула завышает вклад по сравнению с тем, который рассчитан по формуле сложных процентов.
Предел функции
Пусть
функция f
определена в некоторой окрестности
точки ,
кроме, быть может, самой точки
,
кроме, быть может, самой точки
 .
.
Дадим
определение конечного предела функции
y=f(x)
при
 на
языке последовательностей (по Гейне).
на
языке последовательностей (по Гейне).
Определение
18.
Число A
называется пределом
функции
y=f(x)
в
точке
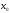 ,
если для любой последовательности точек
,
если для любой последовательности точек
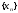 (
(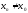 ),
сходящейся к
),
сходящейся к
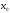 (т.е.
(т.е.
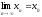 ),
последовательность соответствующих
значений функции
),
последовательность соответствующих
значений функции
 сходится к А.
сходится к А.
Обозначается:
 .
.
Таким
образом,

Геометрический
смысл предела функции
 означает,
что для всех x,
достаточно близких к точке
означает,
что для всех x,
достаточно близких к точке
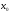 ,
соответствующие значения функции как
угодно мало отличаются от числа А.
,
соответствующие значения функции как
угодно мало отличаются от числа А.
Из определения 18 следует, что функция не может иметь двух различных пределов в одной точке.
Замечание.
Определение
18
предела функции y=f(x)
для
случая, когда аргумент
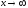 перепишется
в виде:
перепишется
в виде:
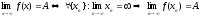
Дадим
еще одно определение конечного предела
функции при
 на
языке «
на
языке «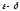 »
(по Коши).
»
(по Коши).
Определение
19.
Число A
называется пределом
функции
y=f(x)
в
точке
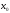 ,
если для любого сколь угодно малого
положительного числа
,
если для любого сколь угодно малого
положительного числа
 можно указать такое положительное число
можно указать такое положительное число
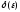 ,
что для всех х,
удовлетворяющих неравенству
,
что для всех х,
удовлетворяющих неравенству
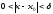 ,
выполняется неравенство
,
выполняется неравенство
 .
.
Таким
образом,
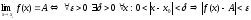 .
.
Определения предела функции в точке по Гейне и по Коши эквивалентны.
Геометрический
смысл определения конечного предела
состоит в следующем: для любой
 -окрестности
точки А
найдется
-окрестности
точки А
найдется
 -окрестность
точки
-окрестность
точки
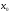 ,
что для всех
,
что для всех
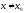 из
этой
из
этой
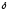 -окрестности
соответствующие значения функции y=f(x)
попадут в
-окрестности
соответствующие значения функции y=f(x)
попадут в
 -окрестность
точки А,
т.е. точки графика функции y=f(x)
будут
заключены в полосе
-окрестность
точки А,
т.е. точки графика функции y=f(x)
будут
заключены в полосе
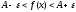 .
.
Замечание.
Для случая, когда аргумент
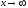 в
определении 19 вместо
в
определении 19 вместо
 пишут
пишут
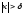 ,
т.е.
,
т.е.
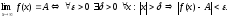
Если
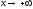 ,
то пишут
,
то пишут
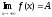 ,
если
,
если
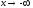 ,
то пишут
,
то пишут
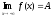 .
.
Теорема
2.
Если
функции f(x)
и g(x)
в точке
 имеют конечные пределы, т.е.
имеют конечные пределы, т.е.
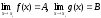 ,
то
,
то
 .
.
Эта теорема верна для любого конечного числа слагаемых и сомножителей.
Следствие
1.
 .
.
Следствие
2.
 .
.
Теорема
3.
Пусть функции
 определены в некоторой окрестности
точки
определены в некоторой окрестности
точки
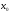 (кроме,
быть может, самой этой точки), и для
всех х
(
(кроме,
быть может, самой этой точки), и для
всех х
(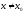 )
из этой окрестности выполняется:
)
из этой окрестности выполняется:
 и
и
 ,
тогда
,
тогда
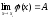 .
.
