- •GfВведение в математический анализ План
- •Множества
- •Операции над множествами
- •Понятие функции, ее области определения и множества значений. Способы задания функции
- •Основные свойства функции
- •Понятие обратной функции
- •Понятие сложной функции
- •Применение функций в экономике
- •Числовые последовательности
- •Предел последовательности
- •Число е, применение в экономике
- •Предел функции
- •Замечательные пределы
- •Бесконечно малые, бесконечно большие функции
- •Классификация бесконечно малых
- •Односторонние пределы функции
- •Непрерывность функции, классификация точек разрыва
- •Основы дифференциального исчисления функции одной переменной План
- •Определение производной
- •Геометрический и физический смысл производной
- •Связь между непрерывностью и дифференцируемостью функции
- •Правила дифференцирования функций
- •Дифференцирование сложной, обратной функций
- •Производная неявной и параметрически заданной функций
- •Определение и геометрический смысл дифференциала
- •Производные высших порядков явно заданной функции
- •Производные высших порядков неявно заданной функции
- •Производные высших порядков параметрически заданной функции
- •Дифференциалы высших порядков
- •Основные теоремы дифференциального исчисления
- •Раскрытие неопределенностей с помощью правила Лопиталя
- •Формула Тейлора
- •Разложение по формуле Маклорена некоторых элементарных функций
- •Исследование функций с помощью производных Условия возрастания и убывания функции
- •Понятие экстремума
- •Выпуклость графика функции. Точки перегиба
- •Асимптоты графика функции
- •Применение производных в экономике
- •Функция нескольких переменных План
- •Определение функции нескольких переменных. Область определения
- •Линии уровня
- •Предел функции нескольких переменных
- •Непрерывность функции нескольких переменных
- •Частные производные первого и высших порядков
- •Полный дифференциал и его применение при приближенных вычислениях
- •Дифференциалы высших порядков
- •Производная по направлению, градиент функции
- •Экстремум функции нескольких переменных
- •Наибольшее и наименьшее значения функции нескольких переменных в замкнутой области
- •Условный экстремум. Метод множителей Лагранжа
- •Метод наименьших квадратов
- •Основы интегрального исчисления План
- •Первообразная функции и неопределенный интеграл
- •Основные свойства неопределенного интеграла
- •Основные методы интегрирования
- •Рациональные дроби
- •Интегрирование простейших рациональных дробей
- •Интегрирование рациональных дробей
- •Интегрирование тригонометрический функций
- •Интегрирование некоторых иррациональных функций
- •Интегралы, не выражающиеся через элементарные функции
- •Определенный интеграл
- •Основные свойства определенного интеграла
- •Определенный интеграл с переменным верхним пределом
- •Формула Ньютона – Лейбница
- •Основные методы вычисления определенного интеграла
- •Геометрические приложения определенного интеграла
- •Некоторые приложения определенного интеграла в экономике
- •Несобственные интегралы
- •Дифференциальные уравнения План
- •Общие сведения о дифференциальных уравнениях
- •Дифференциальные уравнения первого порядка (общие понятия)
- •Уравнения с разделяющимися переменными
- •Однородные дифференциальные уравнения
- •Линейные уравнения. Уравнения я. Бернулли
- •Дифференциальные уравнения второго порядка (основные понятия)
- •Уравнения, допускающие понижение порядка
- •Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Линейные однородные уравнения второго порядка
- •Неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Применение дифференциальных уравнений в задачах экономики
- •Числовые и функциональные ряды План
- •Основные понятия. Сходимость ряда
- •Необходимый признак сходимости
- •Достаточные признаки сходимости рядов с положительными членами
- •Знакочередующиеся ряды. Признак Лейбница
- •Знакопеременные ряды. Общий достаточный признак сходимости знакопеременных рядов
- •Функциональные ряды. Степенные ряды. Сходимость степенных рядов
- •Ряды Тейлора и Маклорена
Понятие обратной функции
Пусть
задана функция y = f(x)
с областью определения D
и множеством значений E.
Если каждому
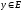 соответствует единственное значение
соответствует единственное значение
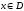 ,
то определена функция
,
то определена функция
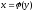 с
областью определения E
и множеством значений D.
Функция
с
областью определения E
и множеством значений D.
Функция
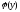 называется
обратной
к
функции
y = f(x)
и записывается:
называется
обратной
к
функции
y = f(x)
и записывается:
 .
.
Справедливо:
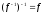 .
Поэтому функции f
и
.
Поэтому функции f
и
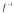 называются
взаимно
обратными.
называются
взаимно
обратными.
Замечание.
Функция y = f(x)
имеет
обратную тогда и только тогда, когда
она взаимно однозначная, т.е. каждому
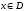 соответствует единственный
соответствует единственный
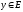 и наоборот. Отсюда следует, что любая
монотонная функция имеет обратную.
и наоборот. Отсюда следует, что любая
монотонная функция имеет обратную.
Правило нахождения обратной функции для взаимно однозначной функции y = f(x):
1.
Из уравнения y = f(x)
выражаем
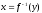 ;
;
2.
Переобозначая
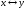 ,
получим функцию
,
получим функцию
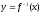 ,
обратную данной.
,
обратную данной.
Графики
взаимно обратных функций y = f(x)
и
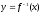 симметричны относительно биссектрисы
первого и третьего координатных углов.
симметричны относительно биссектрисы
первого и третьего координатных углов.
Понятие сложной функции
Пусть
y = f(u)
определена на множестве D,
а функция
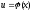 определена
на множестве D1,
причем для
определена
на множестве D1,
причем для
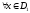 соответствующее значение
соответствующее значение
 .
Тогда на множестве D1
определена функция
.
Тогда на множестве D1
определена функция
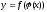 ,
которая называется сложной
функцией
от x
или функцией
от функции
или композицией
функций.
,
которая называется сложной
функцией
от x
или функцией
от функции
или композицией
функций.
Переменную
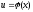 называют промежуточным
аргументом
сложной функции.
называют промежуточным
аргументом
сложной функции.
Можно рассматривать сложные функции от любого количества промежуточных аргументов. Например, сложная функция от 2-х промежуточных аргументов выглядит так:
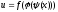 .
.
Пример.
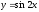 –
сложная функция. Ее можно записать в
виде следующей цепочки равенств:
–
сложная функция. Ее можно записать в
виде следующей цепочки равенств:
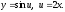
Применение функций в экономике
В экономике наиболее часто используются следующие функции:
1.Функция полезности – зависимость полезности, т.е. результата, эффекта некоторого действия от уровня (интенсивности) этого действия;
2. Производственная функция – зависимость результата производственной деятельности от обусловивших его факторов;
3. Функция выпуска – зависимость объема производства от наличия или потребления ресурсов;
4. Функция издержек – зависимость издержек производства от объема продукции;
5. Функции спроса, потребления и предложения – зависимость объема спроса, потребления и предложения на отдельные товары или услуги от различных факторов (например, цены, дохода и т. д.);
и другие.
Числовые последовательности
Определение
11.
Числовая последовательность – функция
натурального аргумента, т.е. функция
вида
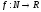 .
.
Числовая
последовательность обозначается:
 или
или
 ,
или
,
или
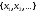 .
.
Числа
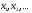 называются
членами последовательности, нижний
индекс означает номер элемента. Число
называются
членами последовательности, нижний
индекс означает номер элемента. Число
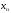 называется
n-м
или общим
членом последовательности,
а формула
называется
n-м
или общим
членом последовательности,
а формула
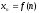 называется
формулой общего
члена последовательности.
называется
формулой общего
члена последовательности.
Так как последовательность является числовой функцией, то к ней применимо большинство понятий, справедливых для числовых функций (ограниченность, монотонность и др.).
Определение
12.
Пусть
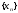 и
и 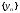 – две
числовые последовательности. Суммой,
разностью, произведением и отношением
этих последовательностей называются
числовые последовательности
– две
числовые последовательности. Суммой,
разностью, произведением и отношением
этих последовательностей называются
числовые последовательности
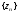 ,
члены которых образованы по правилу:
,
члены которых образованы по правилу:
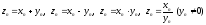 .
.
Предел последовательности
Определение
13.
Число а
называется пределом
числовой
последовательности
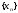 ,
если для любого сколь угодно малого
положительного числа
,
если для любого сколь угодно малого
положительного числа
 найдется такое натуральное число
найдется такое натуральное число
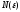 ,
что для всех n > N
члены этой последовательности
удовлетворяют неравенству
,
что для всех n > N
члены этой последовательности
удовлетворяют неравенству
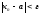 .
.
В
этом случае говорят, что последовательность
имеет предел и пишут:
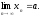
Таким
образом,
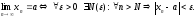
Последовательность,
имеющая предел
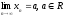 называется сходящейся,
а последовательность, не имеющая
конечного предела, – расходящейся.
называется сходящейся,
а последовательность, не имеющая
конечного предела, – расходящейся.
Неравенство
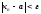 равносильно неравенству
равносильно неравенству
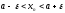 .
.
Определение
14.
Интервал
вида
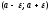 ,
где
,
где
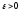 называется
называется
 -окрестностью
или просто окрестностью
точки
а
числовой оси.
-окрестностью
или просто окрестностью
точки
а
числовой оси.
Определение
предела имеет следующий геометрический
смысл: число а
является пределом последовательности
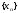 ,
если для любой
,
если для любой
 -окрестности
точки а
найдется натуральное число N,
что все значения
-окрестности
точки а
найдется натуральное число N,
что все значения
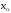 ,
для которых n>N,
попадут в
,
для которых n>N,
попадут в
 -окрестность
точки.
-окрестность
точки.
Ясно,
что чем меньше
 ,
тем больше число N,
но в любом случае внутри
,
тем больше число N,
но в любом случае внутри
 -окрестности
точки а
содержатся почти все члены этой
последовательности,
а вне
окрестности может оказаться лишь
конечное их число.
-окрестности
точки а
содержатся почти все члены этой
последовательности,
а вне
окрестности может оказаться лишь
конечное их число.
Теорема 1. Сходящиеся последовательности обладают следующими свойствами:
1.
сходящаяся последовательность
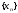 может
иметь только один предел;
может
иметь только один предел;
2.
сходящаяся
последовательность
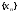 ограничена (обратно: всякая ограниченная
монотонная последовательность сходится);
ограничена (обратно: всякая ограниченная
монотонная последовательность сходится);
3.
если последовательности
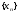 и
и
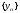 сходятся
к числам a
и b
соответственно, т. е.
сходятся
к числам a
и b
соответственно, т. е.
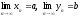 ,
то
,
то
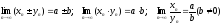 .
.
Определение
15.
Последовательность
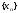 называется бесконечно
большой, если
называется бесконечно
большой, если
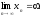
При
этом последовательность называется
положительной
бесконечно большой,
если
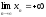 и
отрицательной
бесконечной большой,
если
и
отрицательной
бесконечной большой,
если
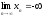 .
.
Определение
16.
Последовательность
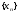 называется бесконечно
малой, если
называется бесконечно
малой, если