
- •GfВведение в математический анализ План
- •Множества
- •Операции над множествами
- •Понятие функции, ее области определения и множества значений. Способы задания функции
- •Основные свойства функции
- •Понятие обратной функции
- •Понятие сложной функции
- •Применение функций в экономике
- •Числовые последовательности
- •Предел последовательности
- •Число е, применение в экономике
- •Предел функции
- •Замечательные пределы
- •Бесконечно малые, бесконечно большие функции
- •Классификация бесконечно малых
- •Односторонние пределы функции
- •Непрерывность функции, классификация точек разрыва
- •Основы дифференциального исчисления функции одной переменной План
- •Определение производной
- •Геометрический и физический смысл производной
- •Связь между непрерывностью и дифференцируемостью функции
- •Правила дифференцирования функций
- •Дифференцирование сложной, обратной функций
- •Производная неявной и параметрически заданной функций
- •Определение и геометрический смысл дифференциала
- •Производные высших порядков явно заданной функции
- •Производные высших порядков неявно заданной функции
- •Производные высших порядков параметрически заданной функции
- •Дифференциалы высших порядков
- •Основные теоремы дифференциального исчисления
- •Раскрытие неопределенностей с помощью правила Лопиталя
- •Формула Тейлора
- •Разложение по формуле Маклорена некоторых элементарных функций
- •Исследование функций с помощью производных Условия возрастания и убывания функции
- •Понятие экстремума
- •Выпуклость графика функции. Точки перегиба
- •Асимптоты графика функции
- •Применение производных в экономике
- •Функция нескольких переменных План
- •Определение функции нескольких переменных. Область определения
- •Линии уровня
- •Предел функции нескольких переменных
- •Непрерывность функции нескольких переменных
- •Частные производные первого и высших порядков
- •Полный дифференциал и его применение при приближенных вычислениях
- •Дифференциалы высших порядков
- •Производная по направлению, градиент функции
- •Экстремум функции нескольких переменных
- •Наибольшее и наименьшее значения функции нескольких переменных в замкнутой области
- •Условный экстремум. Метод множителей Лагранжа
- •Метод наименьших квадратов
- •Основы интегрального исчисления План
- •Первообразная функции и неопределенный интеграл
- •Основные свойства неопределенного интеграла
- •Основные методы интегрирования
- •Рациональные дроби
- •Интегрирование простейших рациональных дробей
- •Интегрирование рациональных дробей
- •Интегрирование тригонометрический функций
- •Интегрирование некоторых иррациональных функций
- •Интегралы, не выражающиеся через элементарные функции
- •Определенный интеграл
- •Основные свойства определенного интеграла
- •Определенный интеграл с переменным верхним пределом
- •Формула Ньютона – Лейбница
- •Основные методы вычисления определенного интеграла
- •Геометрические приложения определенного интеграла
- •Некоторые приложения определенного интеграла в экономике
- •Несобственные интегралы
- •Дифференциальные уравнения План
- •Общие сведения о дифференциальных уравнениях
- •Дифференциальные уравнения первого порядка (общие понятия)
- •Уравнения с разделяющимися переменными
- •Однородные дифференциальные уравнения
- •Линейные уравнения. Уравнения я. Бернулли
- •Дифференциальные уравнения второго порядка (основные понятия)
- •Уравнения, допускающие понижение порядка
- •Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Линейные однородные уравнения второго порядка
- •Неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Применение дифференциальных уравнений в задачах экономики
- •Числовые и функциональные ряды План
- •Основные понятия. Сходимость ряда
- •Необходимый признак сходимости
- •Достаточные признаки сходимости рядов с положительными членами
- •Знакочередующиеся ряды. Признак Лейбница
- •Знакопеременные ряды. Общий достаточный признак сходимости знакопеременных рядов
- •Функциональные ряды. Степенные ряды. Сходимость степенных рядов
- •Ряды Тейлора и Маклорена
Экстремум функции нескольких переменных
Определение
14.
Точка
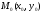 называется точкой максимума
(минимума)
функции
z = f(x;
y),
если существует окрестность точки
называется точкой максимума
(минимума)
функции
z = f(x;
y),
если существует окрестность точки
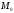 ,
такая, что для всех точек (x;
y)
из этой окрестности, выполняется
неравенство
,
такая, что для всех точек (x;
y)
из этой окрестности, выполняется
неравенство
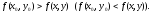
В
определении речь идет о локальном
экстремуме (максимуме и минимуме)
функции, так как речь идет о максимальном
и минимальном значении лишь в достаточно
малой окрестности точки
 .
.
Теорема
4 (необходимое условие экстремума).
Пусть точка
 –
точка экстремума дифференцируемой
функции z = f(x;
y).
Тогда частные производные функции в
этой точке равны нулю, т. е.
–
точка экстремума дифференцируемой
функции z = f(x;
y).
Тогда частные производные функции в
этой точке равны нулю, т. е.
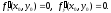
Замечание. Функция может иметь экстремум и в точках, где хотя бы одна из частных производных не существует.
Определение
15.
Точка, в которой частные производные
первого порядка функции z = f(x;
y)
равны
нулю, т. е.
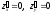 называется
стационарной
точкой функции.
называется
стационарной
точкой функции.
Определение 16. Стационарные точки и точки, в которых хотя бы одна частная производная не существует, называются критическими точками.
Теорема
5 (достаточное условие экстремума).
Пусть в стационарной точке
 и некоторой ее окрестности функция
z = f(x;
y)
имеет непрерывные частные производные
до второго порядка включительно. Вычислим
в точке
и некоторой ее окрестности функция
z = f(x;
y)
имеет непрерывные частные производные
до второго порядка включительно. Вычислим
в точке
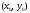 значения
значения
 .
Обозначим:
.
Обозначим:
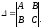
Тогда:
1)
если
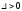 ,
то функция z = f(x;
y)
имеет в точке
,
то функция z = f(x;
y)
имеет в точке
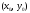 экстремум: максимум, если A<0
и минимум, если A>0.
экстремум: максимум, если A<0
и минимум, если A>0.
2)
если
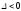 ,
то функция z = f(x;
y)
в точке
,
то функция z = f(x;
y)
в точке
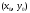 экстремума не имеет;
экстремума не имеет;
3)
если
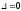 ,
экстремум в
точке
,
экстремум в
точке
 может
быть, а может и не быть. Необходимы
дополнительные исследования.
может
быть, а может и не быть. Необходимы
дополнительные исследования.
Наибольшее и наименьшее значения функции нескольких переменных в замкнутой области
Функция, дифференцируемая в ограниченной замкнутой области D, достигает своего наибольшего (наименьшего) значения или в стационарной точке или в точке границы области. Таким образом, для нахождения экстремума функции в замкнутой области сначала находят все стационарные точки функции внутри области D, а затем наибольшее и наименьшее значения на ее границе. Сравнивая полученные величины, находим наименьшее и наибольшее значения функции в области D.
Условный экстремум. Метод множителей Лагранжа
Если
ищется экстремум функции z = f(x;
y),
при условии, что ее аргументы связаны
между собой уравнением
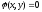 (уравнением
связи),
то говорят об условном
экстремуме.
Для отыскания условного экстремума
воспользуемся методом
неопределенных множителей Лагранжа.
(уравнением
связи),
то говорят об условном
экстремуме.
Для отыскания условного экстремума
воспользуемся методом
неопределенных множителей Лагранжа.
Чтобы
найти условный экстремум функции
z = f(x;
y)
при
наличии уравнения связи
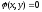 ,
составим функцию Лагранжа
,
составим функцию Лагранжа
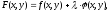
где
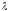 –
неопределенный постоянный множитель,
и найдем обычный экстремум этой
вспомогательной функции.
–
неопределенный постоянный множитель,
и найдем обычный экстремум этой
вспомогательной функции.
Необходимые
условия экстремума функции
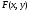 сводятся к системе трех уравнений
сводятся к системе трех уравнений

с
тремя неизвестными
 ,
из которой можно найти эти неизвестные.
Таким образом, решения системы есть
стационарные точки функции Лагранжа.
,
из которой можно найти эти неизвестные.
Таким образом, решения системы есть
стационарные точки функции Лагранжа.
Затем вопрос о существовании и характере условного экстремума решается на основании изучения знака второго дифференциала
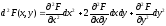
в
стационарной точке функции Лагранжа,
при условии, что
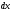 и
и
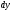 связаны соотношением
связаны соотношением

Функция
z = f(x;
y)
имеет
условный
максимум,
если
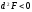 и условной
минимум,
если
и условной
минимум,
если
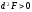 .
В частности, если дискриминант
.
В частности, если дискриминант
 для
функции
для
функции
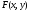 в
стационарной точке положителен, то в
этой точке имеется условный максимум
функции f(x;
y),
если А<0,
и условный минимум, если А>0.
в
стационарной точке положителен, то в
этой точке имеется условный максимум
функции f(x;
y),
если А<0,
и условный минимум, если А>0.
Задача нахождения условного экстремума используется при решении таких экономических задач, как нахождение оптимального распределения ресурсов, выбор оптимального портфеля ценных бумаг и др.
