Полный дифференциал и его применение при приближенных вычислениях

Определение 10. Полным дифференциалом функции z = f(x; y) называется сумма произведений частных производных этой функции на приращения соответствующих независимых переменных, т.е.

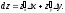(3)

Для функций f(x; y)=x и g(x; y)=y согласно формуле (3) имеем: 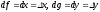. С учетом этого формулу (3) для дифференциала функции z = f(x; y) можно переписать в виде:

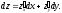(4)

или

()

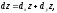где 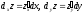– частные дифференциалы функции z = f(x; y).

Определение 11. Функция z = f(x; y) называется дифференцируемой в точке (x; y), если ее полное приращение можно представить в виде:

(5)

где – бесконечно малые при .

Замечание. Отметим, что для функции одной переменной y= f(x) существование конечной производной и представление приращения функции в виде: 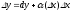, являются равнозначными утверждениями, поэтому любое из них можно брать за определение дифференцируемости функции. Для функции нескольких переменных дело обстоит иначе: существование частных производных является необходимым, но не достаточным условием дифференцируемости функции.

Следующая теорема выражает достаточное условие дифференцируемости функции двух переменных.

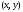Теорема 2. Если частные производные функции z = f(x; y) существуют в окрестности точки и непрерывны в самой точке , то функция дифференцируема в этой точке.

Из формулы (5) следует, что при достаточно малых и 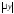имеет место приближенное равенство:

Подставляя выражения для 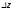из формулы (1) и для 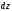из формулы (3), получим

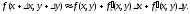(6)

Формула (6) применяется для приближенных вычислений значений функций.

Дифференциалы высших порядков

Полный дифференциал функции называют также дифференциалом первого порядка.

Пусть функция z = f(x; y) имеет непрерывные частные производные второго порядка. Дифференциал второго порядка определяется по формуле: 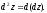Подставляя вместо 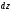его выражение из формулы (4) и дифференцируя его, получим

Аналогично определяется дифференциал третьего порядка: 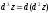. Можно показать, что для дифференциала третьего порядка справедлива формула:

Аналогично находятся дифференциалы четвертого и т. д. порядков.

Производная по направлению, градиент функции

Пусть функция z = f(x; y) определена в некоторой окрестности точки М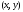, а l – некоторое направление, задаваемое единичным вектором 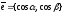, где – углы, образуемые вектором 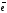с осями координат.

При перемещении в данном направлении l точки М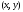 в точку 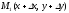функция z = f(x; y) получит приращение

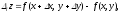
которое называется приращением функции f(x; y) в данном направлении l.

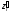
Определение 12. Производной по направлению l функции двух переменных z = f(x; y) называется предел отношения приращения функции в этом направлении к величине приращения , при стремлении последней к нулю, т.е.

(7)

Производная характеризует скорость изменения функции в направлении l.

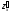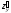Очевидно, что рассмотренные ранее частные производные и представляют собой производные по направлениям, параллельным соответственно осям Ox и Oy.

Можно показать, что

. (8)

Рассмотрим понятие градиента функции z = f(x; y).

Определение 13. Градиентом функции z = f(x; y) называется вектор с координатами 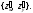Обозначается:или.

Рассмотрим скалярное произведение вектора и единичного вектора , получим

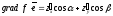. (9)

Сравнивая равенства (8) и (9), получим, что

,

т.е. производная по направлению есть скалярное произведение градиента 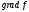и единичного вектора , задающего направление l.

Известно, что скалярное произведение максимально, если они одинаково направлены. Следовательно, градиент функции 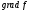в данной точке характеризует направление максимальной скорости изменения функции в этой точке.

Зная градиент функции в каждой точке, можно локально строить линии уровня. Имеет место следующая

Теорема 3. Пусть задана дифференцируемая функция z = f(x; y) и пусть в точке

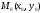величина градиента отлична от нуля. Тогда градиент перпендикулярен линии уровня, проходящей через данную точку.