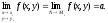- •GfВведение в математический анализ План
- •Множества
- •Операции над множествами
- •Понятие функции, ее области определения и множества значений. Способы задания функции
- •Основные свойства функции
- •Понятие обратной функции
- •Понятие сложной функции
- •Применение функций в экономике
- •Числовые последовательности
- •Предел последовательности
- •Число е, применение в экономике
- •Предел функции
- •Замечательные пределы
- •Бесконечно малые, бесконечно большие функции
- •Классификация бесконечно малых
- •Односторонние пределы функции
- •Непрерывность функции, классификация точек разрыва
- •Основы дифференциального исчисления функции одной переменной План
- •Определение производной
- •Геометрический и физический смысл производной
- •Связь между непрерывностью и дифференцируемостью функции
- •Правила дифференцирования функций
- •Дифференцирование сложной, обратной функций
- •Производная неявной и параметрически заданной функций
- •Определение и геометрический смысл дифференциала
- •Производные высших порядков явно заданной функции
- •Производные высших порядков неявно заданной функции
- •Производные высших порядков параметрически заданной функции
- •Дифференциалы высших порядков
- •Основные теоремы дифференциального исчисления
- •Раскрытие неопределенностей с помощью правила Лопиталя
- •Формула Тейлора
- •Разложение по формуле Маклорена некоторых элементарных функций
- •Исследование функций с помощью производных Условия возрастания и убывания функции
- •Понятие экстремума
- •Выпуклость графика функции. Точки перегиба
- •Асимптоты графика функции
- •Применение производных в экономике
- •Функция нескольких переменных План
- •Определение функции нескольких переменных. Область определения
- •Линии уровня
- •Предел функции нескольких переменных
- •Непрерывность функции нескольких переменных
- •Частные производные первого и высших порядков
- •Полный дифференциал и его применение при приближенных вычислениях
- •Дифференциалы высших порядков
- •Производная по направлению, градиент функции
- •Экстремум функции нескольких переменных
- •Наибольшее и наименьшее значения функции нескольких переменных в замкнутой области
- •Условный экстремум. Метод множителей Лагранжа
- •Метод наименьших квадратов
- •Основы интегрального исчисления План
- •Первообразная функции и неопределенный интеграл
- •Основные свойства неопределенного интеграла
- •Основные методы интегрирования
- •Рациональные дроби
- •Интегрирование простейших рациональных дробей
- •Интегрирование рациональных дробей
- •Интегрирование тригонометрический функций
- •Интегрирование некоторых иррациональных функций
- •Интегралы, не выражающиеся через элементарные функции
- •Определенный интеграл
- •Основные свойства определенного интеграла
- •Определенный интеграл с переменным верхним пределом
- •Формула Ньютона – Лейбница
- •Основные методы вычисления определенного интеграла
- •Геометрические приложения определенного интеграла
- •Некоторые приложения определенного интеграла в экономике
- •Несобственные интегралы
- •Дифференциальные уравнения План
- •Общие сведения о дифференциальных уравнениях
- •Дифференциальные уравнения первого порядка (общие понятия)
- •Уравнения с разделяющимися переменными
- •Однородные дифференциальные уравнения
- •Линейные уравнения. Уравнения я. Бернулли
- •Дифференциальные уравнения второго порядка (основные понятия)
- •Уравнения, допускающие понижение порядка
- •Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Линейные однородные уравнения второго порядка
- •Неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Применение дифференциальных уравнений в задачах экономики
- •Числовые и функциональные ряды План
- •Основные понятия. Сходимость ряда
- •Необходимый признак сходимости
- •Достаточные признаки сходимости рядов с положительными членами
- •Знакочередующиеся ряды. Признак Лейбница
- •Знакопеременные ряды. Общий достаточный признак сходимости знакопеременных рядов
- •Функциональные ряды. Степенные ряды. Сходимость степенных рядов
- •Ряды Тейлора и Маклорена
Определение функции нескольких переменных. Область определения
Пусть задано множество D упорядоченных пар чисел (x, y).
Определение
1. Соответствие
f,
которое каждой паре чисел (x,
y) D
сопоставляет одно и только одно число
z
D
сопоставляет одно и только одно число
z R,
называется функцией
двух переменных,
определенной на множестве D
со значениями в R,
и записывается в виде z=f(x,
y)
или
R,
называется функцией
двух переменных,
определенной на множестве D
со значениями в R,
и записывается в виде z=f(x,
y)
или
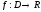 .
.
Величины x и y называются независимыми переменными (аргументами), а z – зависимой переменной (функцией). Множество D=D (f) называется областью определения функции. Множество значений, принимаемых z, называется областью изменения функции и обозначается E(f) или Е.
Функцию
z=f(x,
y),
где (x,
y) D
можно рассматривать как функцию точки
М(x,
y)
координатной плоскости Oxy.
Тогда под областью определения функции
z
понимается
совокупность точек плоскости Oxy,
в которых данная функция z
существует, т.е. принимает определенные
действительные значения. Для характеристики
области D
проще всего указать, какая фигура на
плоскости Oxy
заполняется соответствующими точками.
D
можно рассматривать как функцию точки
М(x,
y)
координатной плоскости Oxy.
Тогда под областью определения функции
z
понимается
совокупность точек плоскости Oxy,
в которых данная функция z
существует, т.е. принимает определенные
действительные значения. Для характеристики
области D
проще всего указать, какая фигура на
плоскости Oxy
заполняется соответствующими точками.
Функция
z=f(x,
y)
двух
независимых переменных допускает
геометрическое истолкование: каждой
точке
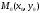 области D
в системе координат
Oxyz
соответствует точка
области D
в системе координат
Oxyz
соответствует точка
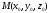 ,
где
,
где
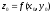 – аппликата точки
– аппликата точки
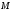 .
Совокупность всех таких точек представляет
собой некоторую поверхность, которая
и будет геометрически изображать данную
функцию z=f(x,
y).
.
Совокупность всех таких точек представляет
собой некоторую поверхность, которая
и будет геометрически изображать данную
функцию z=f(x,
y).
Обобщая функцию двух переменных перейдем к понятию функции от n переменных.
Рассмотрим
точку
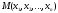 n-мерного
евклидова пространства
n-мерного
евклидова пространства
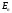 .
.
Определение
2.
Соответствие
f,
которое каждой
точке
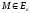 евклидова
пространства сопоставляет
некоторое
число
евклидова
пространства сопоставляет
некоторое
число
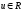 ,
называется функцией
точки
и обозначается u = f(M).
,
называется функцией
точки
и обозначается u = f(M).
Замечание. Всякая функция нескольких переменных становится функцией меньшего числа переменных, если часть переменных зафиксировать.
В качестве примера функций нескольких переменных рассмотрим следующие функции:
1. Функция Кобба–Дугласа
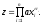
Для
двух переменных она имеет вид:
 .
.
С
помощью функций Кобба–Дугласа строят
производственные функции, выражающие
результат производственной деятельности
в зависимости от различных факторов
 .
.
2.
Функция
полезности для
многомерного случая – это функция
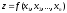 ,
выражающая полезность от n
приобретенных товаров. Чаще всего
встречаются следующие ее виды:
,
выражающая полезность от n
приобретенных товаров. Чаще всего
встречаются следующие ее виды:
a)
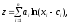 где
где
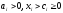 – логарифмическая
функция;
– логарифмическая
функция;
б)
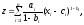 где
где
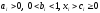 .
Такая функция называется функцией
постоянной эластичности.
.
Такая функция называется функцией
постоянной эластичности.
Линии уровня
Определение 3. Линией уровня функции z = f(x; y) называется множество всех точек плоскости Oxy, в которых функция z принимает постоянное значение, то есть f(x; y) = С, где С – постоянная.
Число С в этом случае называется уровнем.
Линия уровня может быть получена при пересечении графика функции z=f(x, y) с плоскостью z=С, параллельной плоскости Oxy. Затем эту линию следует спроектировать на плоскость Oxy.
Предел функции нескольких переменных
Определение
4.
 окрестностью
точки
окрестностью
точки
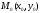 называется
круг радиуса
называется
круг радиуса
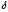 ,
содержащим точку
,
содержащим точку
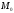 внутри себя.
внутри себя.
На
плоскости Oxy
введем расстояние между точками
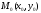 и
и
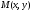 :
:
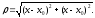
Тогда
условие нахождения точки M
внутри круга радиуса
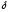 является выполнение неравенства
является выполнение неравенства
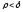 .
.
Определение
5.
Число а
называется пределом
функции
z = f(x;
y)
при
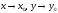 (или в точке
(или в точке
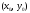 ),
если любого для числа
),
если любого для числа
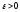 найдется число
найдется число
 ,
такое, что для всех точек
,
такое, что для всех точек
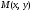 отличных от точки
отличных от точки
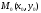 и отстоящих от этой точки на расстояние
и отстоящих от этой точки на расстояние
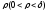 ,
выполняется неравенство
,
выполняется неравенство
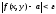 .
.
Обозначается: