Понятие экстремума

Определение 5. Точка называется точкой максимума (минимума) функции y = f(x), если существует такая окрестность точки , что для всех x () из этой окрестности выполняется неравенство .

Значение функции в точке максимума (минимума) функции называется максимумом (минимумом) данной функции.

Максимум (минимум) функции называется экстремумом этой функции, а точки максимума и минимума – точками экстремума.

Теорема 7 (необходимое условие экстремума). Если функция y = f(x) непрерывна в некоторой окрест­ности точки и имеет в этой точке экстремум, то ее произ­водная в этой точке равна нулю или не существует.

Точки, в которых производная функции y = f(x) обращается в нуль или не существует, называются критическими точками или точками возможного экстремума. Точки, в которых производная функции y = f(x) обращается в нуль, называются стационарными.

Теорема 8 (достаточное условие экстремума). Пусть – критическая точка непрерывной функции y = f(x). Если при переходе через точку меняет свой знак с «+» на «–», то – точка максимума; если при переходе через точку меняет свой знак с «–» на «+», то – точка минимума.

Замечание. Экстремум функции называется также локальным экстремумом, в отличие от глобального экстремума – наибольшего (наименьшего) значения, которое функция может принимать в области ее определения. Чтобы найти глобальный экстремум функции y = f(x), заданный на отрезке [a; b], нужно сравнить значения f(a), f(b) с ее значениями в точках возможного экстремума на [a; b] и выбрать наибольшее (наименьшее) из них.

Выпуклость графика функции. Точки перегиба

Определение 6. График дифференцируемой функции y = f(x) называется выпуклым вниз (выпуклым вверх) на интервале (а, b), если он целиком расположен выше (ниже) касательной, проведенной в любой точке этого интервала.

Определение 7. Точка графика дифференцируемой функции y = f(x), в которой направление выпуклости меняется на противоположное, называется точкой перегиба.

Интервалы выпуклости вниз и вверх находятся с помощью следующей теоремы.

Теорема 9. Если функция y = f(x) во всех точках интервала (а, b) имеет отрицательную вторую производную, т.е. , то график функции на этом интервале выпуклый вверх. Если же , то график функции выпуклый вниз.

Для нахождения точек перегиба графика функции используется следующая

Теорема 10 (достаточное условие существования точек перегиба). Если для функции y = f(x) вторая производная в некоторой точке равна нулю или не существует и при переходе через нее меняет свой знак, то точка является точкой перегиба графика функции.

Асимптоты графика функции

Асимптотой кривой называется прямая, к которой неограни­ченно приближается точка кривой при неограниченном уда­лении ее от начала координат.

Асимптоты могут быть вертикальными и наклонными (горизонтальными).

Определение 8. Прямая 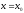называется вертикальной асимптотой графика функции y = f(x), если хотя бы один из односторонних пределов в точке равен бесконечности, т.е. или .

Очевидно, что непрерывные на R функции вертикальных асимптот не имеют; такие асимптоты существуют только в точках разрыва второго рода функции y = f(x).

Определение 9. Прямая y=kx+b называется наклонной (если k=0 – горизонтальной) асимптотой графика функции y = f(x) при (), если функцию f(x) можно представить в виде , где .

Теорема 11. Для того чтобы график функции y = f(x) имел наклонную асимптоту y=kx+b, необходимо и достаточно, чтобы существовали конечные пределы:

. (13)

Замечание. При нахождении наклонных асимптот графика функции возможны следующие случаи: 1) оба предела (13) существуют и не зависят от знака бесконечности, тогда прямая y=kx+b называется двусторонней асимптотой; 2) оба предела (13) существуют, но при и при они различны, тогда имеем две односторонние наклонные асимптоты; 3) если хотя бы один из пределов (13) не существует, то наклонных асимптот нет.