Порядок розв’язання задачі

1. Накреслити схему навантаження елементарного кубика матеріалу і по ній встановити знаки напружень.

2. Провести перепозначення напружень відповідно до правил опору матеріалів.

3. Зобразити ортогональну проекцію елемента та показати напруження _, _, _, _, які діють на двох взаємно перпендикулярних площадках (ортогональної проекції).

4. Визначити головні напруження ₁, ₂, ₃.

5. Знайти положення головних площадок та показати лінії дії головних напружень (на ортогональній проекції).

6. Визначити найбільші дотичні напруження та положення площадок, на яких вони діють.

7. Обчислити величини повних відносних деформацій.

8. Знайти величину відносної зміни об’єму.

9. Обчислити значення питомої потенціальної енергії деформації.

10. Провести перевірку міцності матеріалу: для крихкого стану матеріалу — за теорією міцності Мора, а для пластичного стану матеріалу — за четвертою теорією міцності.

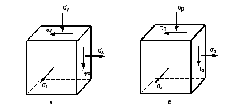
а б

Рис. 2.2

Приклад. Потрібно:

1) виконати перепозначення напружень відповідно до правил опору матеріалів;

2) визначити головні напруження;

3) знайти положення головних площадок і показати лінії дії головних напружень;

4) визначити значення найбільших дотичних напружень і показати площадки, на яких вони діють;

5) виконати перевірку міцності матеріалів;

Дані для розрахунку:

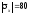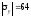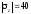МПа; МПа; МПа;

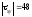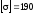МПа; матеріал - сталь Ст.30; МПа.

Розв’язання:

1. Перепозначаємо напруження по гранях паралелепіпеда за правилами опору матеріалів. При цьому має бути .

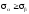Дамо напруженням нові позначення, які діють не на головних площадках (рис. 2.2, б). Отже, маємо:

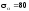МПа; МПа;

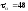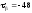МПа; МПа.

2. Визначаємо значення головних напружень. Головні напруження нумеруємо так, щоб виконувалась умова 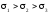. Значення головних напружень знаходимо за формулою

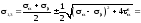
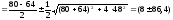МПа.

Отже,

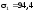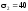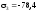МПа, МПа, МПа.

3. Розрахуємо положення головних площадок. Для цього використовуємо формулу

.

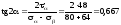Отже, , .

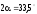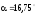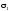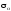Положення головних площадок і лінії дії головних напружень зображені на рис. 2.3. Щоб отримати лінію дії головного напруження , потрібно від лінії дії напруження відкласти кут за ходом годинникової стрілки (якщо кут додатний).

4. Знаходимо значення найбільшого дотичного напруження 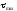за формулою

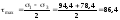МПа.

Щоб отримати напрямок нормалі до площадки, на якій діє напруження 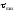, треба від напрямку головного напруження відкласти кут 45 проти ходу годинникової стрілки (рис. 2.3).

5. Виконаємо перевірку міцності матеріалу використовуючи третю теорію міцності. Маємо:

.

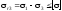У цьому випадку:

,

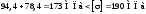тобто умова міцності за третьою теорією міцності виконується. Для сталі Ст. 30 залишкове відносне подовження при розриві = 21 %. Тому цей матеріал є пластичним і для перевірки його міцності можна скористатися третьою теорією міцності.

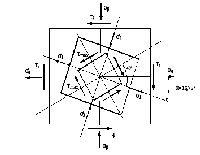
Рис. 2.3

3. Геометричні характеристики плоских перерізів.

3.1 Обчислення геометричних характеристик плоских перерізів.

Задача 4. Для складного перерізу (рис. 3.1) потрібно визначити величини головних центральних моментів інерції і положення головних центральних осей.

Дані для розрахунку наведені в табл. 3.1.

Таблиця 3.1

Варіант	Двотавр №	Швелер №	Кутик №	Лист b × t, мм		Варіант	Двотавр №	Швелер №	Кутик №	Лист b × t, мм
1	20	14	5(3)*	250 × 10		16	30	24	9(6)	420 × 12
2	22	16	5(5)	270 × 10		17	33	27	9(8)	440 × 14
3	24	18	5,6(5)	290 × 10		18	36	30	10(12)	460 × 14
4	27	20	6,3(5)	310 × 10		19	40	33	10(14)	480 × 16
5	30	22	6,4(6)	330 × 10		20	50	40	22(14)	500 × 16
6	33	24	10(8)	350 × 10		21	18	12	5,6(4)	260 × 10
7	36	27	11(8)	370 × 10		22	20	16	7(5)	300 × 10
8	40	30	14(10)	390 × 14		23	22	18	7(8)	320 × 10
9	45	33	14(12)	400 × 14		24	24	20	8(6)	340 × 10
10	50	36	20(12)	450 × 14		25	27	22	8(8)	360 × 12
11	18	12	5,6(4)	260 × 10		26	30	24	9(6)	420 × 12
12	20	16	7(5)	300 × 10		27	33	27	9(8)	440 × 14
13	22	18	7(8)	320 × 10		28	36	30	10(12)	460 × 14
14	24	20	8(6)	340 × 10		29	40	33	10(14)	480 × 16
15	27	22	8(8)	360 × 12		30	50	40	22(14)	500 × 16

Примітка: Розміри та характеристики профілів взяти за Держстандартом.

Зірочкою (*) позначена товщина стінки кутика

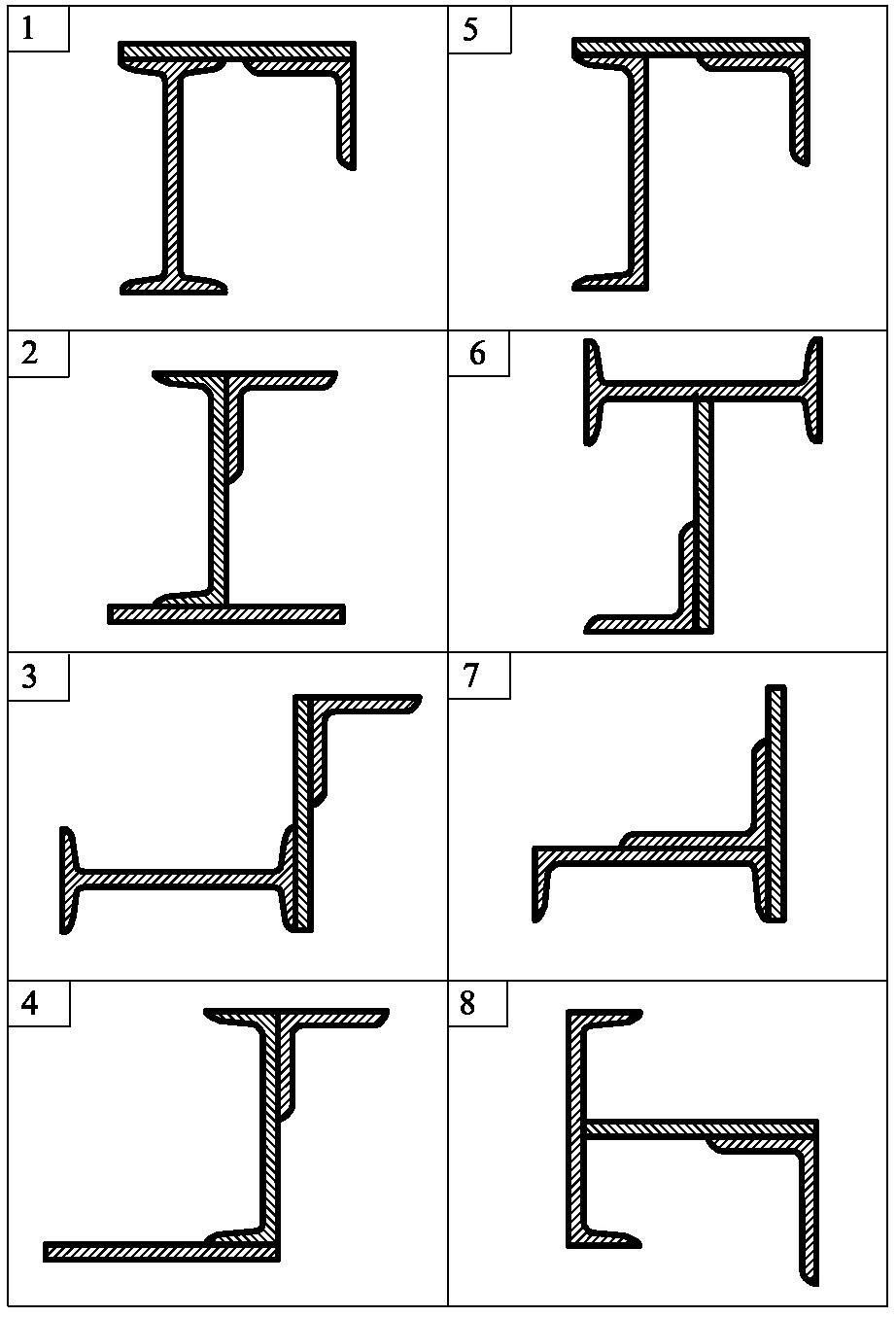Рис. 3.1

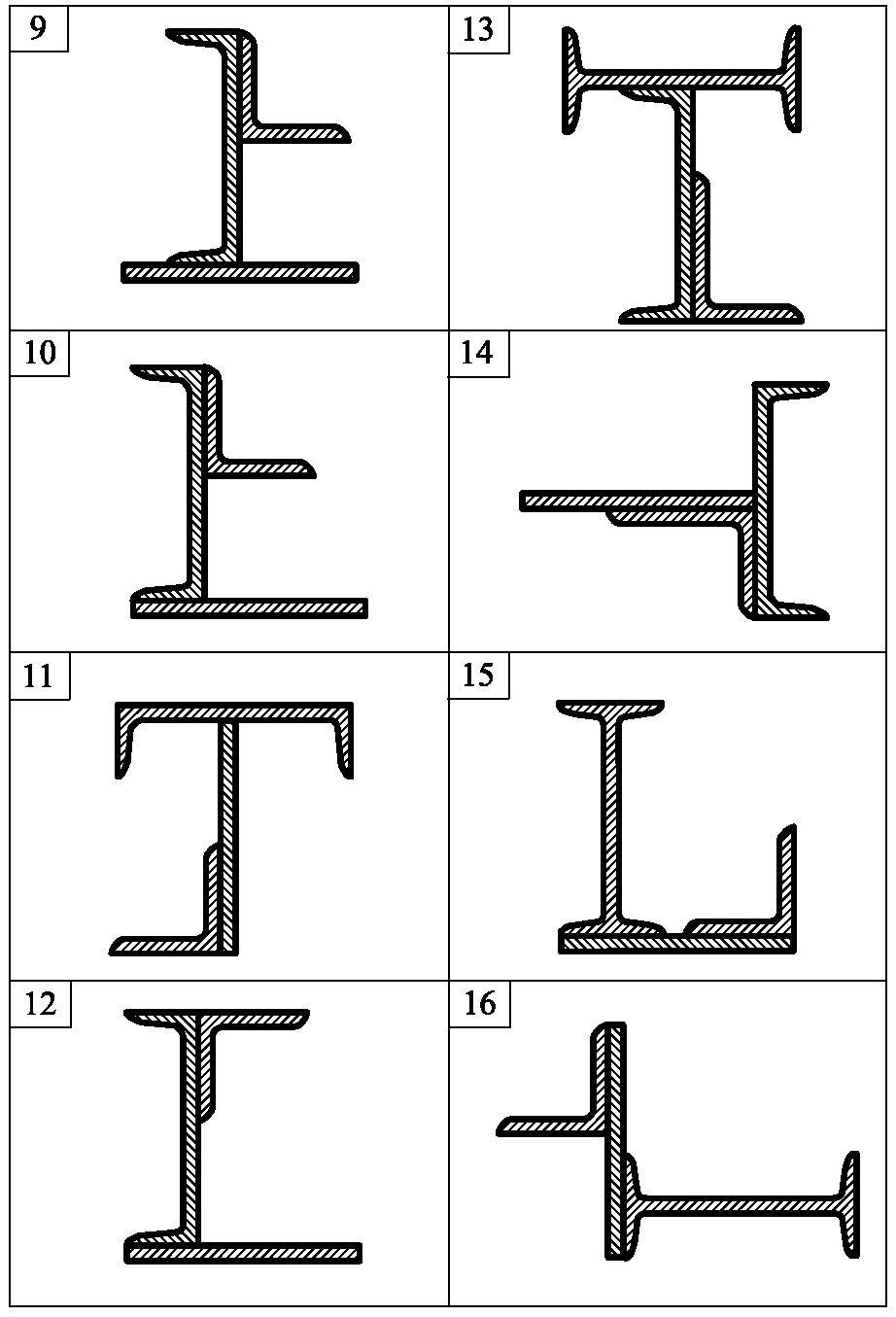
Рис. 3.1

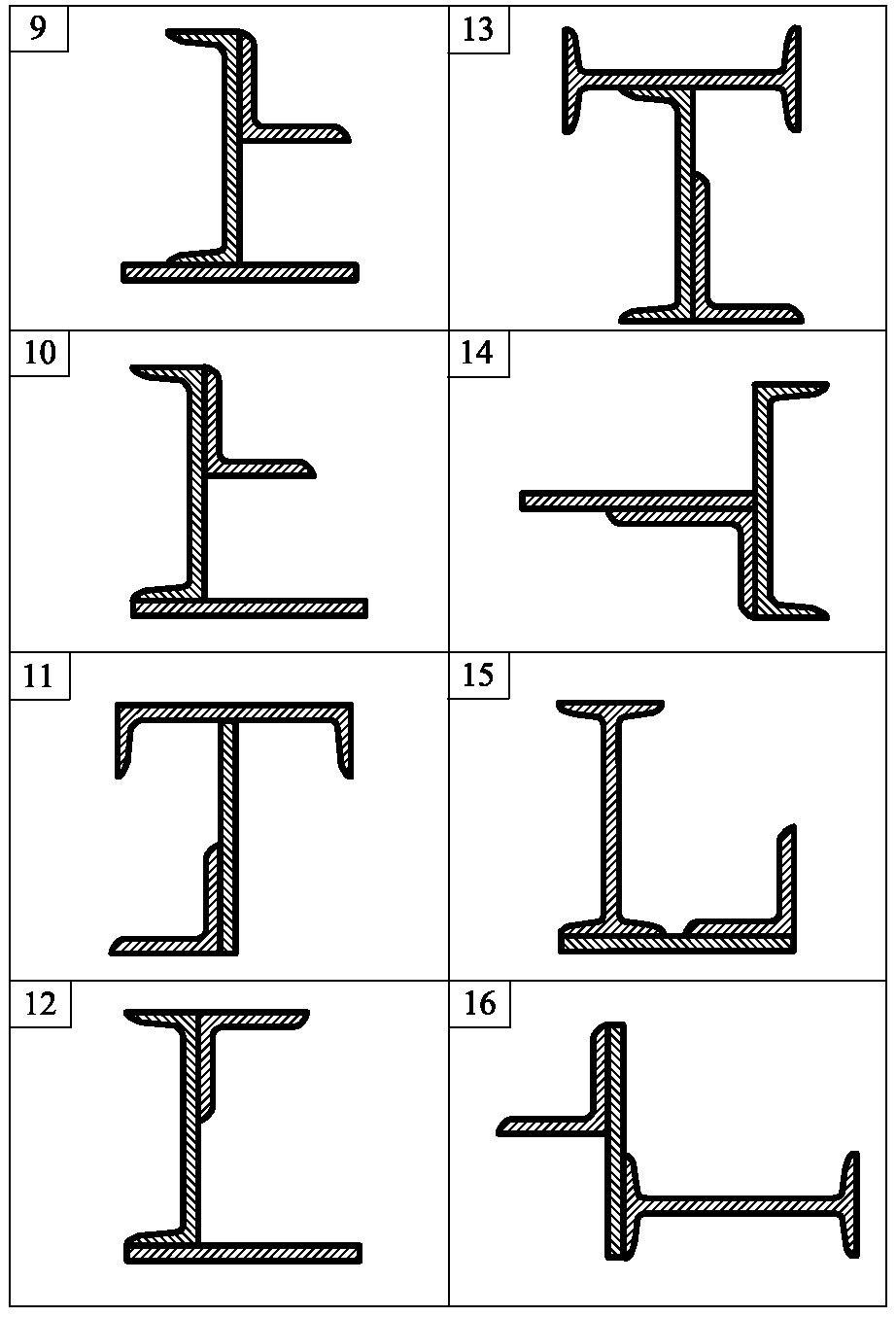
Рис. 3.1

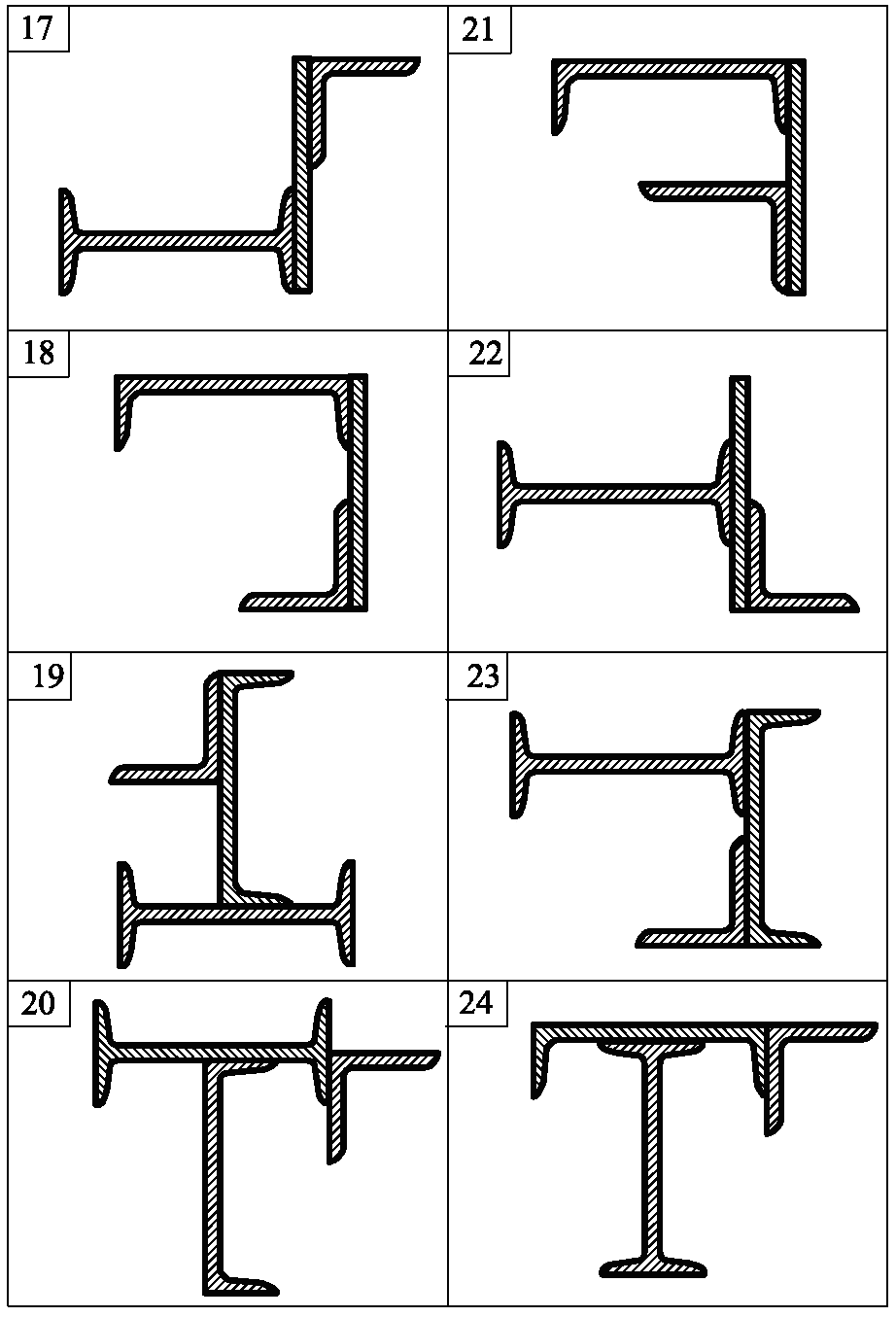
Рис. 3.1

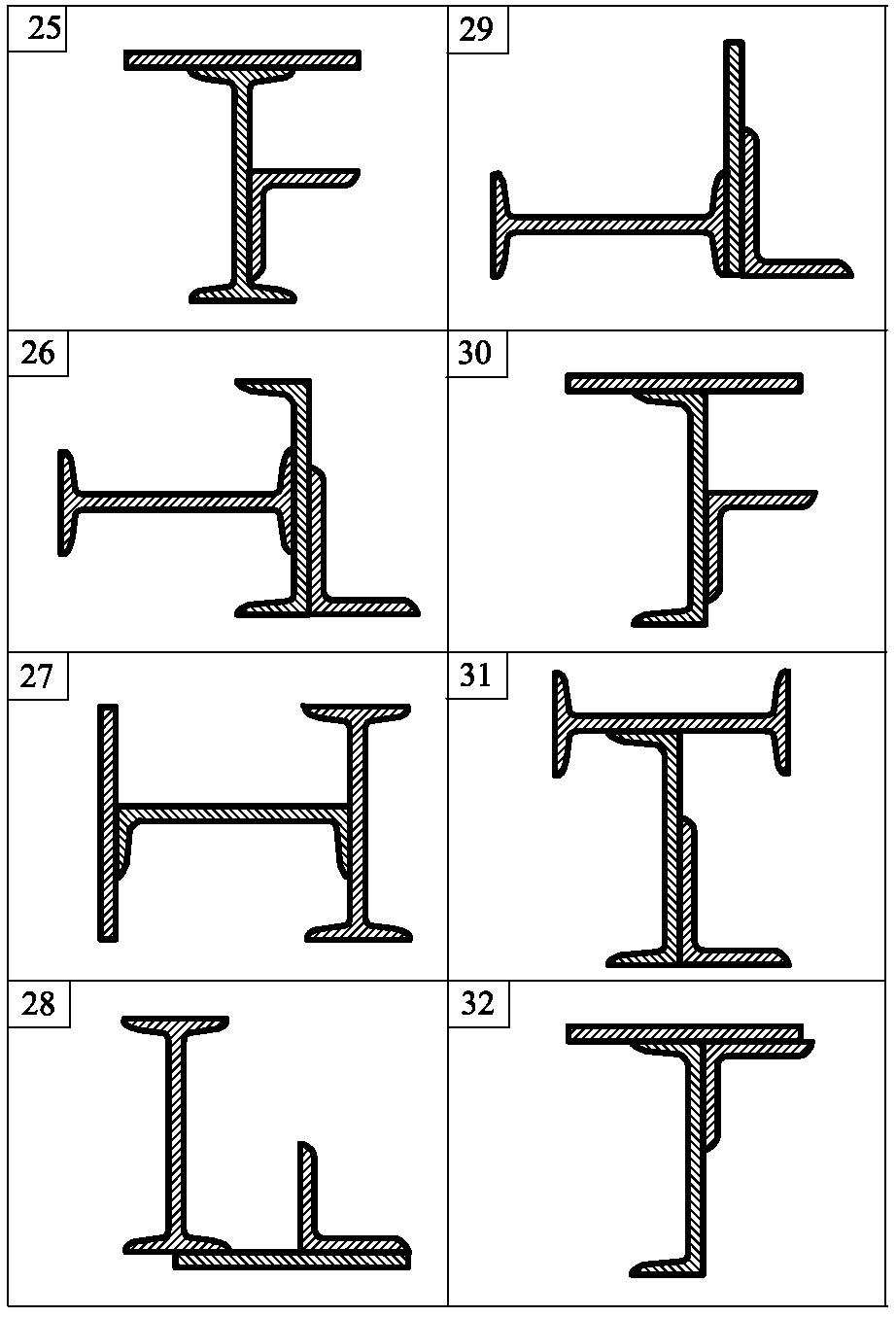
Рис. 3.1 Закінчення