18.2. Визначення залишкової довговічності елемента конструкції
Визначення кількості циклів до руйнування (залишкову довговічність) і аналіз стану елемента при варіації початкової довжини тріщини розглянемо для конструктивного елемента за наявності концентратора напружень і тріщини (рис. 18.5), на який діє асиметричний цикл навантаження.
Дані
для розрахунку: матеріал Д16; механічні
характеристики матеріалу
критичний коефіцієнт інтенсивності
напружень
МПа·м
,
умовна границя текучості
=
400 МПа, найбільший коефіцієнт інтенсивності
напружень циклу при швидкості поширення
тріщини 10
м/цикл,
МПа·м
,
параметр n = 4; коефіцієнт асиметрії
циклу r = 0,33; максимальна інтенсивність
навантаження
140 МПа; ширина елемента
2W = 20 см; висота елемента 2h = 40 см; товщина елемента t = 2 мм; радіус отвору R = 1см.
Величину
(
)
визначаємо за формулою
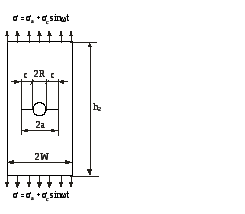
Рис. 18.5
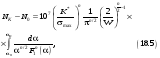де
різниця (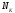
-
)
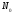являє собою залишкову довговічність
елемента конструкції з тріщиною;
,
.
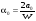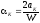Критичну
довжину тріщини
розраховуємо з умови руйнування Ірвіна,
коли
(рис. 18.3). У цьому випадку
,
,
=
0,63.
Використовуючи формулу Сімпсона, обчислюємо інтеграл, що входить у вираз (18.5).
Вводимо позначення:
.
Тоді
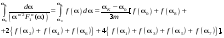
(18.6)
де
m = 8, m + 1 – кількість вузлових
точок, у яких відомі значення підінтегральної
функції ƒ(
).
Для
обчислення поправкової функції F1(
),
яка залежить від геометрії елемента і
тріщини, використовується графік (рис.
18.2) і табл. 18.1. Розрахунок роблять у
табличній формі. Так, для початкової
довжини тріщини
отримано результати, наведені в табл.
18.3. Підставляючи значення ƒ(
)
у вираз (18.6), обчислюємо величину інтеграла
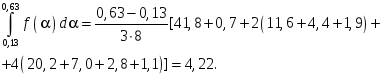
Після розрахунку значення інтеграла, за формулою (18.5) визначаємо число циклів, яке витримає такий конструктивний елемент до руйнування
Таблиця 18.3.
|
і |
аі, см |
|
F1() |
|
|
0 |
1,300 |
0,130 |
1,091 |
41,8 |
|
1 |
1,925 |
0,193 |
1,075 |
20,2 |
|
2 |
2,550 |
0,255 |
1,074 |
11,6 |
|
3 |
3,175 |
0,318 |
1,091 |
7,0 |
|
4 |
3,800 |
0,380 |
1,119 |
4,4 |
|
5 |
4,425 |
0,443 |
1,158 |
2,8 |
|
6 |
5,050 |
0,505 |
1,203 |
1,9 |
|
7 |
5,675 |
0,568 |
1,284 |
1,1 |
|
8 |
6,300 |
0,630 |
1,374 |
0,7 |
Примітка.
Аналогічні
обчислення можна зробити і при інших
значеннях початкової довжини тріщини
.