
- •Опір матеріалів
- •В.В. Астанін….
- •Передмова
- •Оформлення розрахунково-проектної роботи
- •1. Розтягання-стискання
- •1.1 Розрахунок статично визначуваного бруса
- •Порядок розв’язання задачі
- •Приклад. Розрахункова схема показана на рис. 1.2
- •1.2. Розрахунок статично невизначуваного бруса
- •Порядок розв’язання задачі
- •2. Теорія напруженого стану
- •2.1 Дослідження напруженого стану в точці
- •Порядок розв’язання задачі
- •3. Геометричні характеристики плоских перерізів.
- •3.1 Обчислення геометричних характеристик плоских перерізів.
- •Порядок розв’язання задачі
- •4. Плоске згинання
- •4.1 Побудова епюр поперечної сили q і згинального моменту м.
- •Порядок розв’язання задачі
- •4.2. Розрахунок балки на міцність
- •5. Зсув і Кручення
- •5.1. Розрахунок заклепкового з’єднання
- •5.2 Розрахунок зварного з’єднання
- •5.3. Розрахунок вала на міцність і жорсткість
- •Порядок розв’язання задачі
- •Задача 4
- •6. Складний опір
- •6.1. Ламаний стержень
- •Порядок розв’язання задачі
- •6.2 Похила балка
- •Порядок розв’язання задачі
- •6.3. Просторовий ламаний стержень
- •Порядок розв’язання задачі
- •6.4. Згинання з крученням
- •Порядок розв’язання задачі
- •Розрахунок вала на згинання з крученням
- •6.5. Косе згинання
- •Порядок розв’язання задачі
- •Розрахунок балки на косе згинання
- •6.6. Позацентрове стискання
- •Порядок розв’язання задачі
- •Порядок розв’язання задачі
- •Розрахунок ступінчастої колони на позацентрове стискання
- •6.7. Тонкостінний стержень
- •Порядок розв’язання задачі
- •Розрахунок тонкостінного стержня відкритого профілю на позацентрове стискання
- •7. Статично невизначувані системи
- •7.1. БАлка на пружній основі
- •Порядок розв’язання задачі
- •12. На рисунку накреслити задану схему балки і під нею розташувати епюри , m, q і р.
- •Застосування методу скінченних різниць до розрахунку балок на пружній основі
- •Розрахунок балки на пружній основі
- •374,6 КНм 224,6 кНм або Мmах Мрозр,
- •641,5 КНм 665,3 кНм або Мmах Мрозр.,
- •7.2. Визначення переміщень
- •Порядок розв’язання задачі
- •Визначення переміщень методом безпосереднього інтегрування диференціального рівняння зігнутої осі балки
- •Визначення переміщень балок за методом початкових параметрів
- •Визначення переміщень за допомогою інтеграла Мора і правила Верещагіна
- •7.3 Статично невизначувана рама
- •Порядок розв’язання задачі
- •Розрахунок рами методом сил
- •8. Спеціальні задачі міцності
- •8.1. Поздовжнє згинання
- •Порядок розв’язання задачі
- •Приклади розрахунків елементів конструкцій на стійкість
- •8.2. Динамічна дія навантаження
- •8.2.1 Напруження і деформації при ударі
- •Порядок розв’язання задачі
- •Приклад 3
- •1. Спочатку розв’язуємо задачу без урахування маси балки
- •8.2.2 Розрахунок складної балочної конструкції при ударній дії навантаження.
- •8.2.3 Вільні коливання систем з одним ступенем вільності
- •Порядок розв’язання задачі
- •Розрахунок балки на змушені коливання
- •Вільні і вимушені коливання систем з двома ступенями вільності
- •8.3Перевірка міцності та визначення довговічності конструктивного елемента з тріщиною
- •8.4. Розрахунок вала на витривалість
- •Порядок розв’язання задачі
- •Розрахунок вала на витривалість
- •9. Розрахунок конструкцій за несучою здатністю
- •9.1. Згинання балки з ідеального пружно-пластичного матеріалу
- •9.2. Pозрахунoк ступінчастих брусів за несучою здатністю
- •17. Напруження і деформації в наслідок повзучості
- •17.1. Підбір поперечного перерізу балки при повзучості
- •18. Механіка руйнування
- •18.1. Розрахунок залишкової міцності елемента конструкції за наявності концентратора напружень і тріщини
- •18.2. Визначення залишкової довговічності елемента конструкції
Порядок розв’язання задачі
1. Накреслити розрахункову схему балки і показати на ній реакції опор.
2. Визначити величини опорних реакцій.
3. Визначити величини згинальних моментів в характерних перерізах від заданого навантаження та побудувати епюру.
4. Накреслити схему балки і прикласти одиничну силу в точці С.
5. Визначити величину згинального моменту від одиничної сили та побудувати його епюру.
Визначення переміщень методом безпосереднього інтегрування диференціального рівняння зігнутої осі балки
При
використанні цього методу будемо
виходити з
диференціального рівняння (6.17). Щоб
одержати рівняння прогинів z
і рівняння кутів повороту
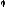 ,
необхідно провести
інтегрування рівняння (6.17),
в результаті чого дістанемо:
,
необхідно провести
інтегрування рівняння (6.17),
в результаті чого дістанемо:
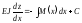 ,
,
інтегруючи ще раз, маємо:
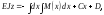
де C і D сталі інтегрування.
Таким чином, отримані рівняння кутів повороту
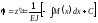
і рівняння прогинів
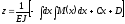 .
.
Сталі інтегрування C і D визначаються з граничних умов. Загальна кількість сталих інтегрування дорівнює подвоєній кількості ділянок балки.
Розглянемо приклади застосування цього методу.
Приклад 1 (рис. 6.33). Маємо:
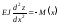 .
.
У цьому випадку
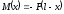 .
.
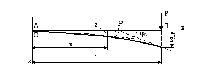
Рис. 6.33
Отже, диференціальне рівняння зігнутої осі балки в розглянутому випадку набуває вигляду:
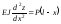 .
(6.22)
.
(6.22)
Рівняння (6.22) інтегруємо два рази:
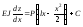 ;
;
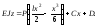
Для
визначення сталих C
і D
використовуємо граничні умови при
х = 0 z
= 0 і
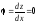 .
Враховуючи ці умови, знаходимо:
.
Враховуючи ці умови, знаходимо:
C = 0 і D = 0.
Таким чином, одержуємо рівняння кута повороту
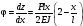 (6.23)
(6.23)
і рівняння прогину
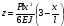 .
(6.24)
.
(6.24)
За
формулами (6.23) і (6.24) можна визначити кут
повороту
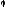 і прогин z
в будь-якому перерізі балки, яка
розглядається. Найбільшого значення
ці величини досягають у даному випадку
на правому кінці балки, тобто при
x = l.
Маємо:
і прогин z
в будь-якому перерізі балки, яка
розглядається. Найбільшого значення
ці величини досягають у даному випадку
на правому кінці балки, тобто при
x = l.
Маємо:
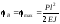 ;
;
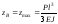 .
.
Приклад 2. (рис. 6.34). Маємо:
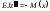 .
.
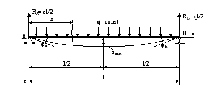
Рис. 6.34
Для балки, яку розглядаємо,
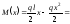
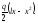
Отже,
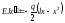 .
(6.25)
.
(6.25)
Інтегруючи рівняння (6.25), одержуємо:
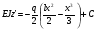 ;
;
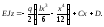 (6.26)
(6.26)
Граничні умови в даному випадку мають вигляд:
при х = 0 z = 0, при х = l z = 0.
Таким чином, з рівняння (6.26) маємо:
D
= 0;
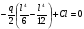 .
.
Звідси
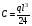 .
.
Формули
для визначення значень z
і
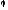 тепер набудуть такого вигляду:
тепер набудуть такого вигляду:
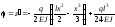 ;
;
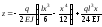
або остаточно
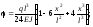
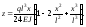
Найбільші кути повороту перерізів у даному випадку будуть у перерізах А і В, тобто на опорах.
Маємо:
при
х
= 0
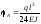 ;
;
при
x
= l
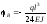
Найбільший прогин буде в середині прольоту балки, тобто при х = l/2. Маємо:
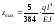 .
.
Для спрощення обчислень (за наявності декількох ділянок навантаження балки) необхідно дотримуватись таких правил:
1) відлік абсцис всіх ділянок слід вести від одного початку координат крайньої лівої (або правої) точки осі балки;
2) при обчисленні згинальних моментів необхідно розглядати ту частину балки, яка містить початок координат;
3)
інтегрування диференціального рівняння
слід виконувати без розкриття дужок
виду
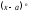 .
.
Визначення переміщень балок за методом початкових параметрів
При визначенні переміщень балок методом безпосереднього інтегрування необхідно складати вирази для згинальних моментів, проводити інтегрування диференціального рівняння зігнутої осі балки і знаходити значення сталих інтегрування. Загальна кількість сталих інтегрування дорівнює подвоєної кількості ділянок балки. Тому при двох чи більшій кількості ділянок балки застосування методу безпосереднього інтегрування стає надто важким. Цих недоліків позбавлений метод п о ч а т к о в и х п а р а м е т р і в, який не потребує складання виразів згинальних моментів та інтегрування диференціального рівняння зігнутої осі балки. Кількість же сталих, які підлягають визначенню при користуванні цим методом, не перевищує двох, незалежно від кількості ділянок балки. Метод початкових параметрів розроблений ученими О.М. Криловим, М.П. Пузиревським та ін.
Інтегруючи диференціальне рівняння зігнутої осі балки (6.20)
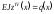
знаходимо
рівняння зігнутої осі балки
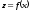 ,
не обчислюючи попередньо значення
моменту M
і поперечної сили Q.
,
не обчислюючи попередньо значення
моменту M
і поперечної сили Q.
Маючи
рівняння зігнутої осі
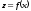 ,
можна визначити значення M
і Q
у будь-якому перерізі за формулами:
,
можна визначити значення M
і Q
у будь-якому перерізі за формулами:
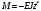 ;
;
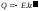 .
(6.27)
.
(6.27)
Загальний розв’язок лінійного неоднорідного диференціального рівняння (6.20) може бути подано у вигляді суми загального розв’язання однорідного рівняння
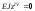 .
(6.28)
.
(6.28)
і
будь-якого частинного розв’язання
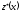 неоднорідного рівняння (6.20).
неоднорідного рівняння (6.20).
Загальний розв’язок рівняння (6.28) знайдемо, інтегруючи його чотири рази:
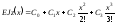 ,
(6.29)
,
(6.29)
де
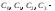 чотири довільні сталі.
чотири довільні сталі.
Введемо
сталі
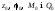 ,
які називаються п о ч а т к о в и- м и п
а р а м е т р а м и, що виникають унаслідок
деформації балки, оскільки одні з них
виражають зусилля, які діють у перерізі
,
які називаються п о ч а т к о в и- м и п
а р а м е т р а м и, що виникають унаслідок
деформації балки, оскільки одні з них
виражають зусилля, які діють у перерізі
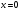 ,
інші переміщення в перерізі
,
інші переміщення в перерізі
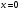 .
У даному випадку, наприклад,
.
У даному випадку, наприклад,
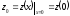 .
.
Диференціюючи
рівняння (6.29), використовуючи формулу
(6.27) і допускаючи, що
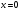 ,
отримуємо залежності між сталими
,
отримуємо залежності між сталими
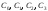 і початковими параметрами
і початковими параметрами
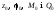 :
:
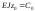 ,
,
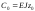 ;
;
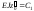 ,
,
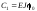 ;
;
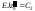 ,
,
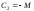 ;
;
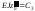 ,
,
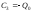 .
.
Враховуючи отриманий результат, формулу (6.29) перепишемо у такому вигляді:
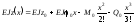 .
(6.30)
.
(6.30)
Загальний
розв’язок неоднорідного рівняння
(6.20) складається із загального розв’язку
однорідного рівняння (6.28), який був
прийнятий у формі виразу (6.30), а також
із частинного розв’язку
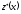 неоднорідного рівняння (6.20). Цей частинний
розв’язок
неоднорідного рівняння (6.20). Цей частинний
розв’язок
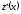 можна знайти або методом варіації
сталих, або методом Коші.
можна знайти або методом варіації
сталих, або методом Коші.
Скористуємося
методом Коші. Відповідно до цього методу
потрібно знайти розв’язок
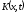 однорідного рівняння (6.28), який залежить
від параметра t,
що задовольняє такі умови:
однорідного рівняння (6.28), який залежить
від параметра t,
що задовольняє такі умови:
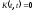 ;
;
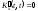 ;
;
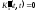 ;
;
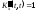 .
.
У даному випадку
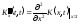 .
.
Тоді частинний розв’язок неоднорідного рівняння (6.20) буде мати такий вигляд:
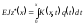 .
.
Неважко перевірити, що в даному випадку
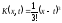 .
.
Відповідно частинний розв’язок неоднорідного диференціаль-ного рівняння (6.20) можна прийняти у формі:
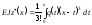 .
(6.31)
.
(6.31)
Використовуючи формулу
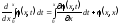 ,
,
знаходимо:
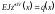 .
.
Отже,
функція
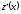 ,
яка визначається формулою (6.31), дійсно
є частинним розв’язком неоднорідного
рівняння (6.20). У формулі (6.31) інтегрування
виконаємо від початку координат (лівого
кінця балки) до точки х,
в якій обчислюється значення функції
z(x).
,
яка визначається формулою (6.31), дійсно
є частинним розв’язком неоднорідного
рівняння (6.20). У формулі (6.31) інтегрування
виконаємо від початку координат (лівого
кінця балки) до точки х,
в якій обчислюється значення функції
z(x).
Таким чином, загальний розв’язок неоднорідного диференціального рівняння (6.20) може бути подано в такій формі:
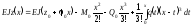 .
(6.32)
.
(6.32)
Розглянемо деякі окремі види навантаження (рис. 6.35)
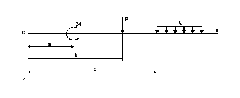
Рис. 6.35
1. Якщо до балки прикладемо рівномірно розподілене навантаження інтенсивністю q при х > c, тоді після розв’язання виразу (6.31) в цьому випадку знаходимо:
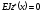 при х
< c;
при х
< c;
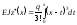 при х
> c.
при х
> c.
Поклавши,
що
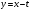 ,
одержимо
,
одержимо
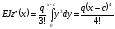 при х
> c.
при х
> c.
Таким чином,
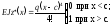 (6.33)
(6.33)
Вираз (6.33) можна подати ще і в такому вигляді:
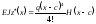 ,
,
де Н(х) одинична функція Хевисайда.
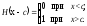
2. Якщо балка навантажена при x = b зосередженою силою Р, то частинне розв’язання (6.31) у цьому випадку (рис. 6.36) дає:
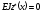 при х
< b;
при х
< b;
Рис.
6.36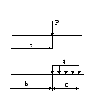
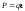 ;
;
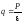 ;
0
;
0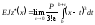 при х
> b.
при х
> b.
Використовуючи теорему про середнє значення
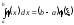 ,
,
де а < < b, одержимо
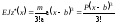
при
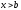 .
.
Отже, остаточно маємо:
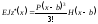 .
.
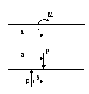
3. Якщо балка навантажена при х = а зосередженим моментом М, тоді частинне розв’язання рівняння (6.31) у цьому випадку (рис. 6.37) буде:
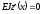 при х
< а;
при х
< а;
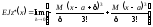
при х > а, або
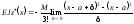 при х
> а.
при х
> а.
Нехай
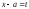 Тоді після заміни змінної отримаємо:
Тоді після заміни змінної отримаємо:
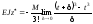 при t
> 0.
при t
> 0.
Через те що
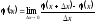 ,
,
то
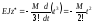 при t
> 0.
при t
> 0.
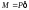 ;
;
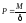 ;
0. Рис. 6.37
;
0. Рис. 6.37
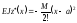 при
при
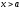 .
.
Отже,
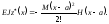
Якщо
на балку будуть діяти декілька зосереджених
моментів
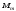 ,
декілька зосереджених сил
,
декілька зосереджених сил
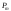 і декілька ділянок рівномірно розподіленого
навантаження інтенсивністю
і декілька ділянок рівномірно розподіленого
навантаження інтенсивністю
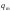 ,
то рівняння зігнутої осі балки (6.32) можна
подати у такому вигляді:
,
то рівняння зігнутої осі балки (6.32) можна
подати у такому вигляді:
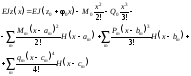 (6.34)
(6.34)
де
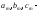 абсциси точок прикладення зосереджених
пар сил
абсциси точок прикладення зосереджених
пар сил
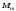 ,
сил
,
сил
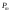 відповідно, початків рівномірно
розподілених навантажень інтенсивністю
відповідно, початків рівномірно
розподілених навантажень інтенсивністю
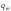 .
У формулі (6.34) припускається, що початок
координат співпадає з лівим кінцем
балки.
.
У формулі (6.34) припускається, що початок
координат співпадає з лівим кінцем
балки.
Два
початкових параметри із чотирьох у
формулі (6.34) є відомими при будь-якому
методі обпирання лівого кінця балки.
Дійсно, для затиснутого лівого кінця
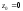 і
і
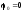 для шарнірно-опертого лівого кінця
для шарнірно-опертого лівого кінця
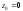 і
і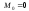 для вільного кінця відомі
для вільного кінця відомі
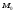 і
і
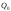 .
Невідомі один або два початкових
параметри знаходять з умов закріплення
інших перерізів балки.
.
Невідомі один або два початкових
параметри знаходять з умов закріплення
інших перерізів балки.
Розглянемо приклади застосування методу початкових параметрів.
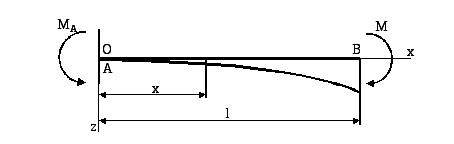
Рис. 6.38
Приклад
1. Для
балки (рис. 6.38) знайти рівняння прогинів
і кутів повороту а також значення прогину
і кута повороту перерізу в точці В.
У
даному випадку початкові параметри
дорівнюють:
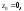
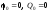 ;
;
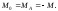
З урахуванням цього вираз (6.34) приймає вигляд:
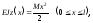
звідси:
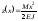
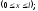
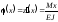
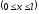 .
.
При x = l маємо:
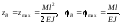
Приклад 2. Для заданої консольної балки знайти рівняння прогинів і кутів повороту, а також значення прогину і кута повороту перерізу в точці В (рис. 6.39).
У даному випадку маємо:
 Рис.
6.39
Рис.
6.39
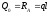 .
.
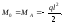
Отже, на основні рівняння (6.34) у даному випадку отримаємо:
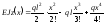
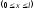 ;
;
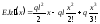
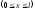 .
.
Отже, остаточно одержуємо рівняння прогинів і кутів повороту перерізу:
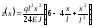
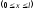 ;
;
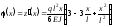
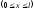 .
.
При x = l маємо:
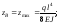
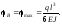
Приклад 3. Для балки на двох опорах знайти рівняння прогинів і кутів повороту, а також значення прогину в перерізі під силою Р (рис. 6.40).
Для балки, яка розглядається
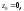
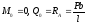 ,
,
 – невідомо.
– невідомо.
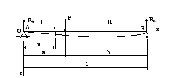
Рис. 6.40
Для
ділянки I
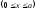 :
:
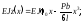
для
ділянки II
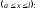
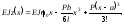
Для
визначення
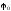 використаємо умову: при x
= l
z
= 0.
використаємо умову: при x
= l
z
= 0.
Отже,
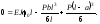
Звідси визначаємо
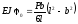 .
.
Таким чином:
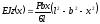
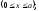
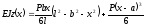
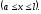
Визначаємо прогин перерізу під силою, тобто при x = a:
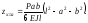
В тому
окремому випадку, коли
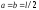 ,
маємо:
,
маємо:
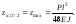
Приклад
4. Застосуємо метод початкових параметрів
до визначення переміщень в перерізах
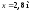 і
і
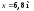 для балки, зображеної на рис. 6.41.
для балки, зображеної на рис. 6.41.
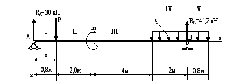
Рис. 6.41
Дано: Р = 32 кН, q = 14 кН/м, m = 16 кНм.
(Балка
двотавр №22. Для якої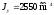 ).
).
Розв’язання:
В даному випадку
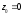 ,
,
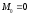 ,
,
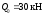 .
Невідомий початковий параметр
.
Невідомий початковий параметр
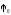 .
.
Рівняння зігнутої осі балки буде мати вигляд:
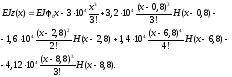
Невідомий
початковий параметр
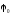 можна визначити із умови на опорі В,
при x=8,8
м, z=0. На відрізку
можна визначити із умови на опорі В,
при x=8,8
м, z=0. На відрізку
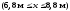
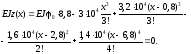
Задовольняючи умову на опорі В, отримаємо рівняння
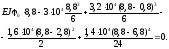
Звідси
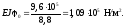
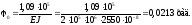
Підставляючи
знайдене значення
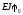 у рівняння зігнутої осі балки, дістаємо
остаточне рівняння у такому вигляді:
у рівняння зігнутої осі балки, дістаємо
остаточне рівняння у такому вигляді:
для
ділянки I
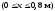
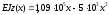 ;
;
для
ділянки II
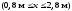
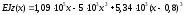 ;
;
для
ділянки III
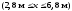
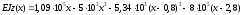 ;
;
для
ділянки IV
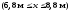
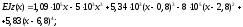
для
ділянки V
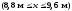
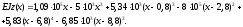
За допомогою цих рівнянь можна визначити прогин у будь-якому перерізі балки. Розрахуємо, наприклад, прогини балки в перерізах при x=2,8 м та x=6,8 м.
Використовуючи рівняння II-ї ділянки, маємо:
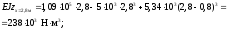
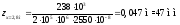
Використовуючи рівняння III-ї ділянки, маємо:
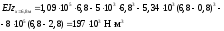
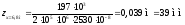 .
.
