6.5. Косе згинання

Задача 11. Для зображеної на рис. 10 балки підібрати розміри поперечного перерізу. Визначити положення нейтральної лінії та побудувати епюру нормальних напружень в небезпечному перерізі балки. Прийняти [σ] = 160 МПа. Дані для розрахунку наведені в таблиці 10. Навантаження прикладені так, що закручування балки не відбувається.

Таблиця 10

Варіант	Сила F, кН	Згинальний момент М, кН · м	Довжи-на а, м		Варіант	Сила F, кН	Згинальний момент М, кН · м	Довжина а, м
1	5	7,5	1,5		16	8	7,5	1,7
2	6	8,4	1,4		17	9	8,4	1,6
3	7	9,1	1,3		18	10	9,1	1,4
4	8	9,6	1,2		19	5	9,6	1,5
5	9	9,9	1,1		20	6	9,9	1,6
6	10	10,0	1,0		21	5	10,0	1,5
7	5	8,0	1,6		22	6	8,0	1,4
8	6	10,2	1,7		23	7	10,2	1,3
9	7	12,6	1,8		24	8	12,6	1,2
10	8	14,0	1,9		25	9	14,0	1,1
11	9	7,5	2,0		26	10	7,5	1,0
12	10	8,4	1,3		27	5	8,4	1,6
13	5	9,1	2,0		28	6	9,1	1,7
14	6	9,6	1,9		29	7	9,6	1,8
15	7	9,9	1,8		30	8	9,9	1,9

Порядок розв’язання задачі

1. Накреслити розрахункову схему балки в аксонометрії. Показати на ній опорні реакції.

2. Визначити величини опорних реакцій, що діють в вертикальній та горизонтальній площинах.

3. Визначити величини згинальних моментів, що утворюються в вертикальній та горизонтальній площинах. Побудувати їхні епюри.

4. Визначити найбільш небезпечний переріз балки і за рівнянням міцності обчислити необхідну величину моменту опору.

5. Знайти розміри поперечного перерізу балки.

6. Визначити положення нейтральної лінії.

7. Обчислити величини нормальних напружень в характерних точках поперечного перерізу.

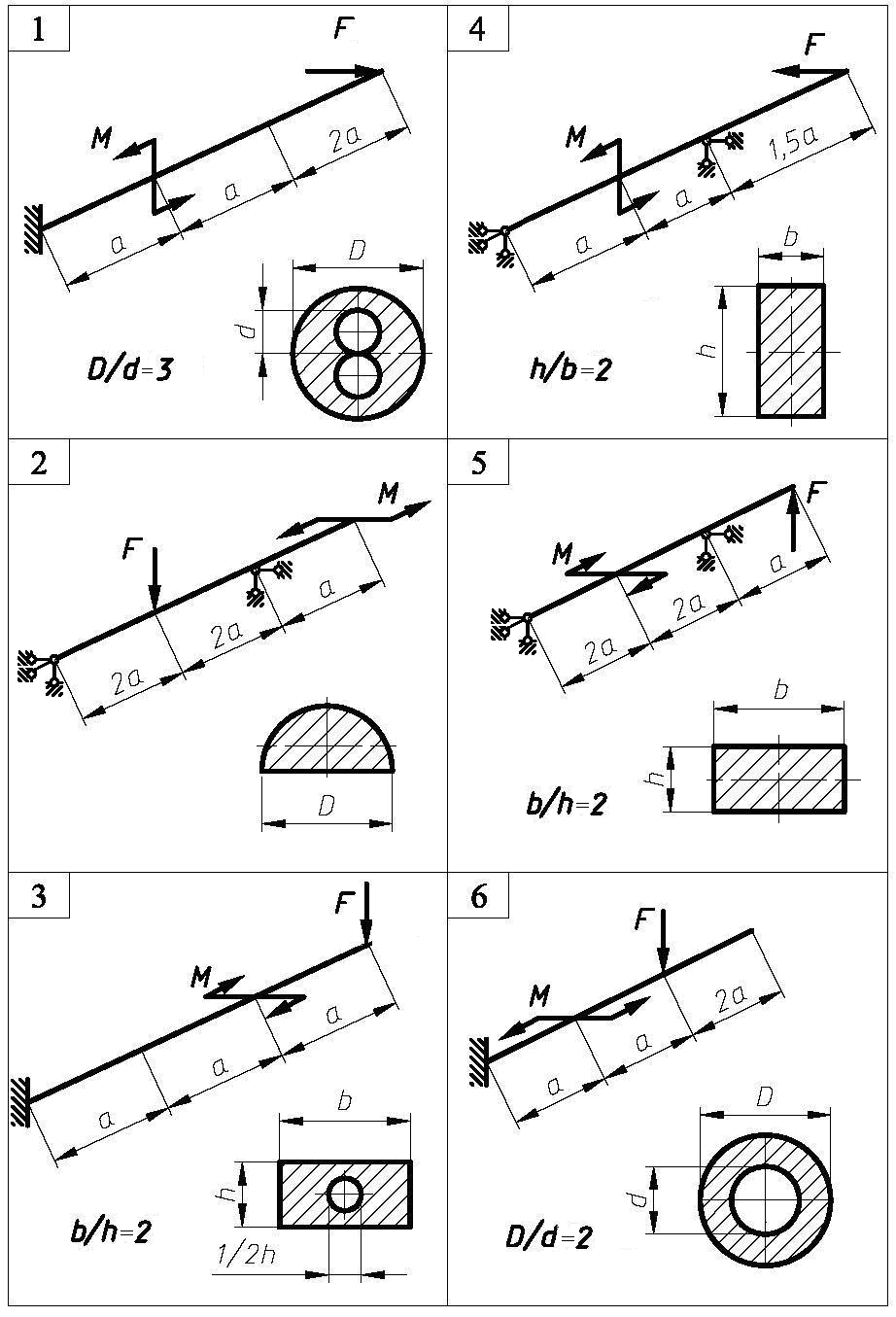
Рис. 10

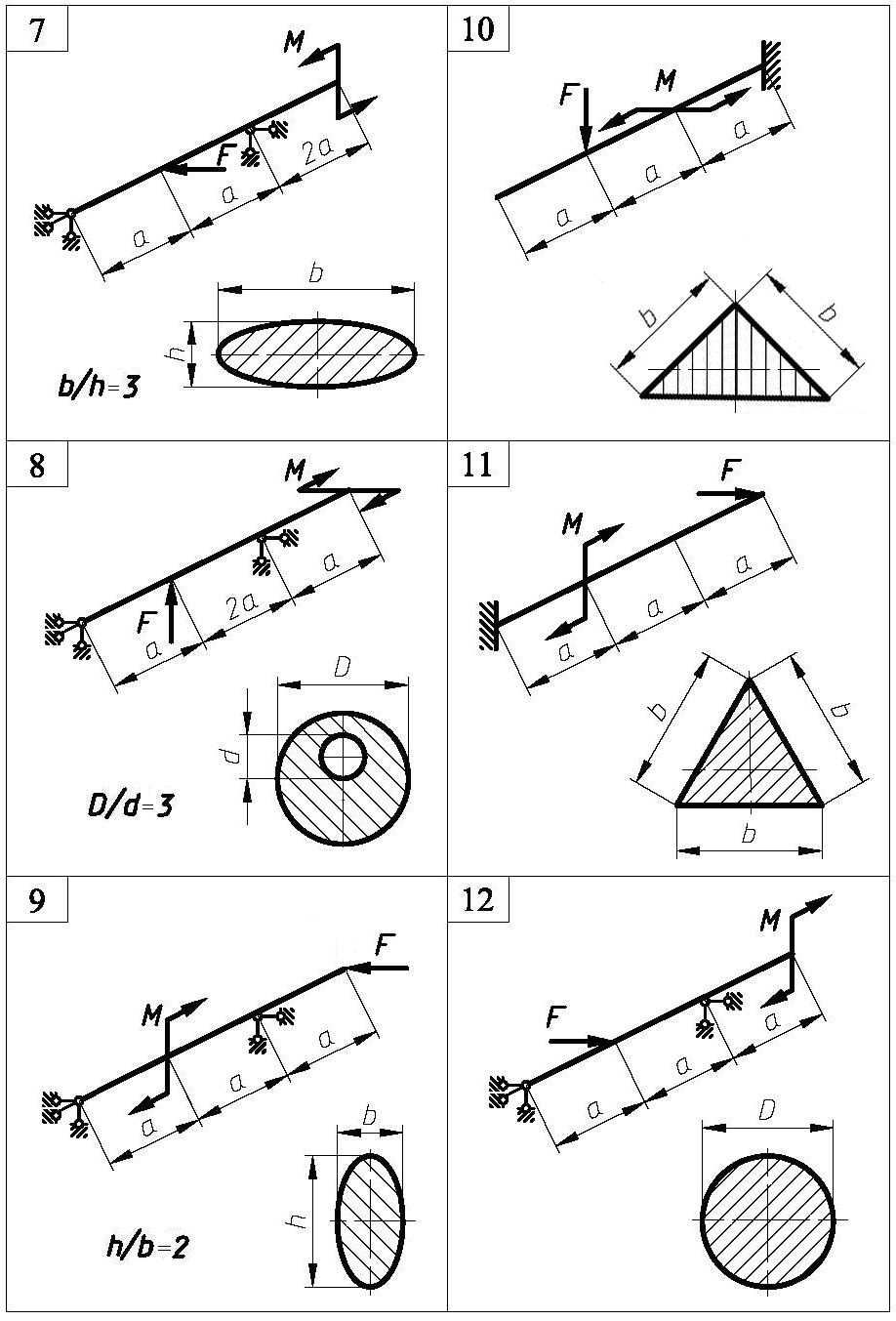
Рис. 10

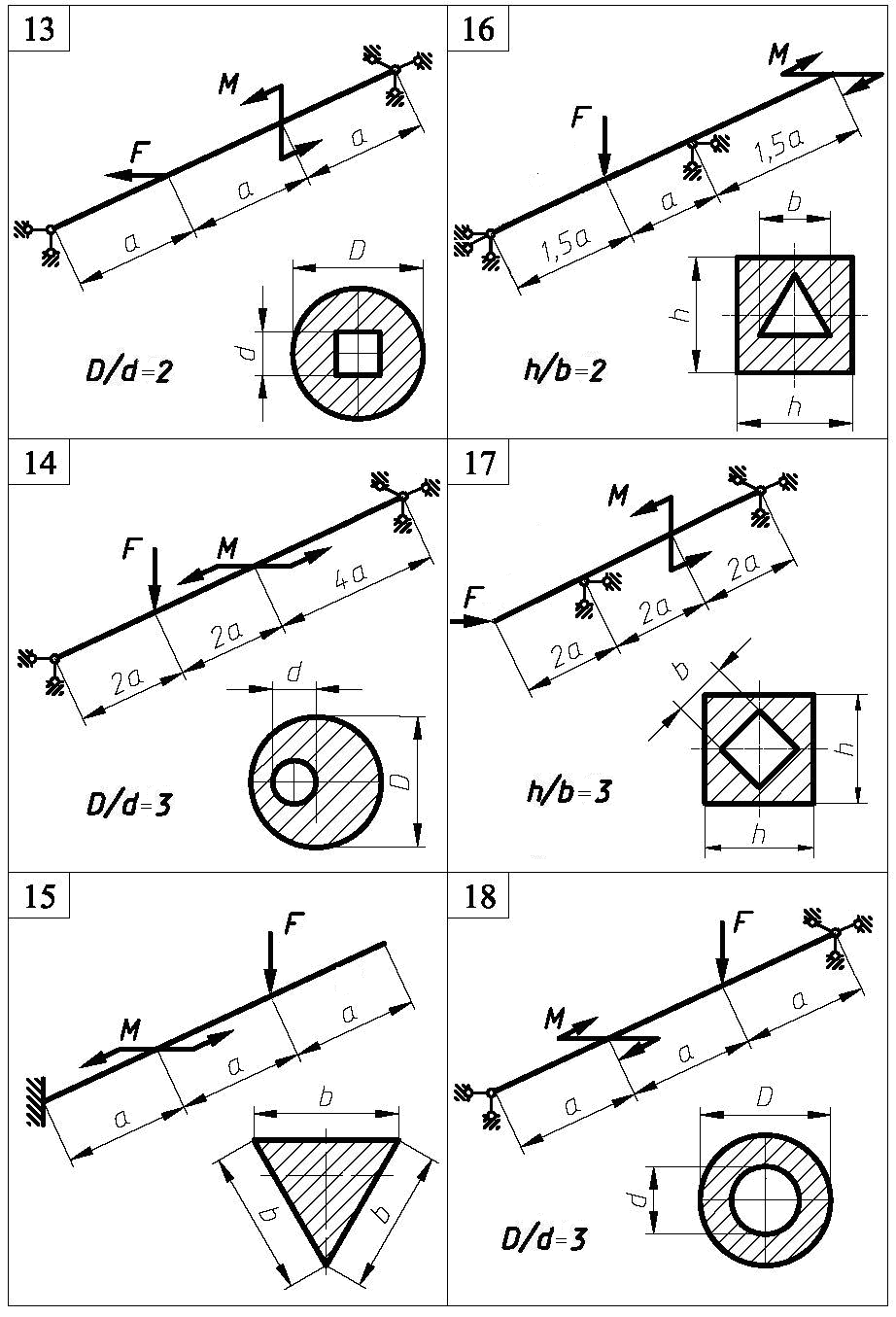
Рис. 10

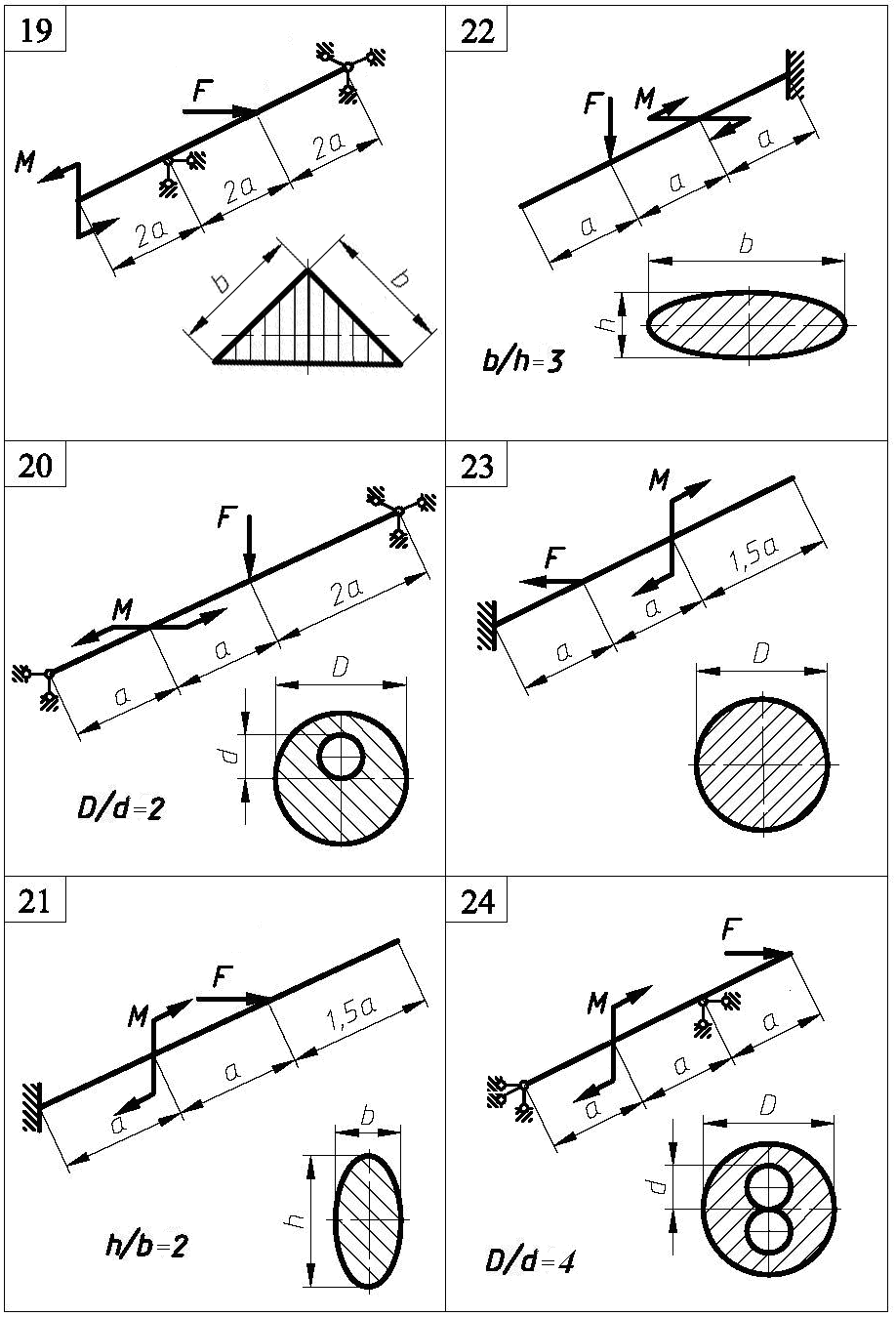
Рис. 10

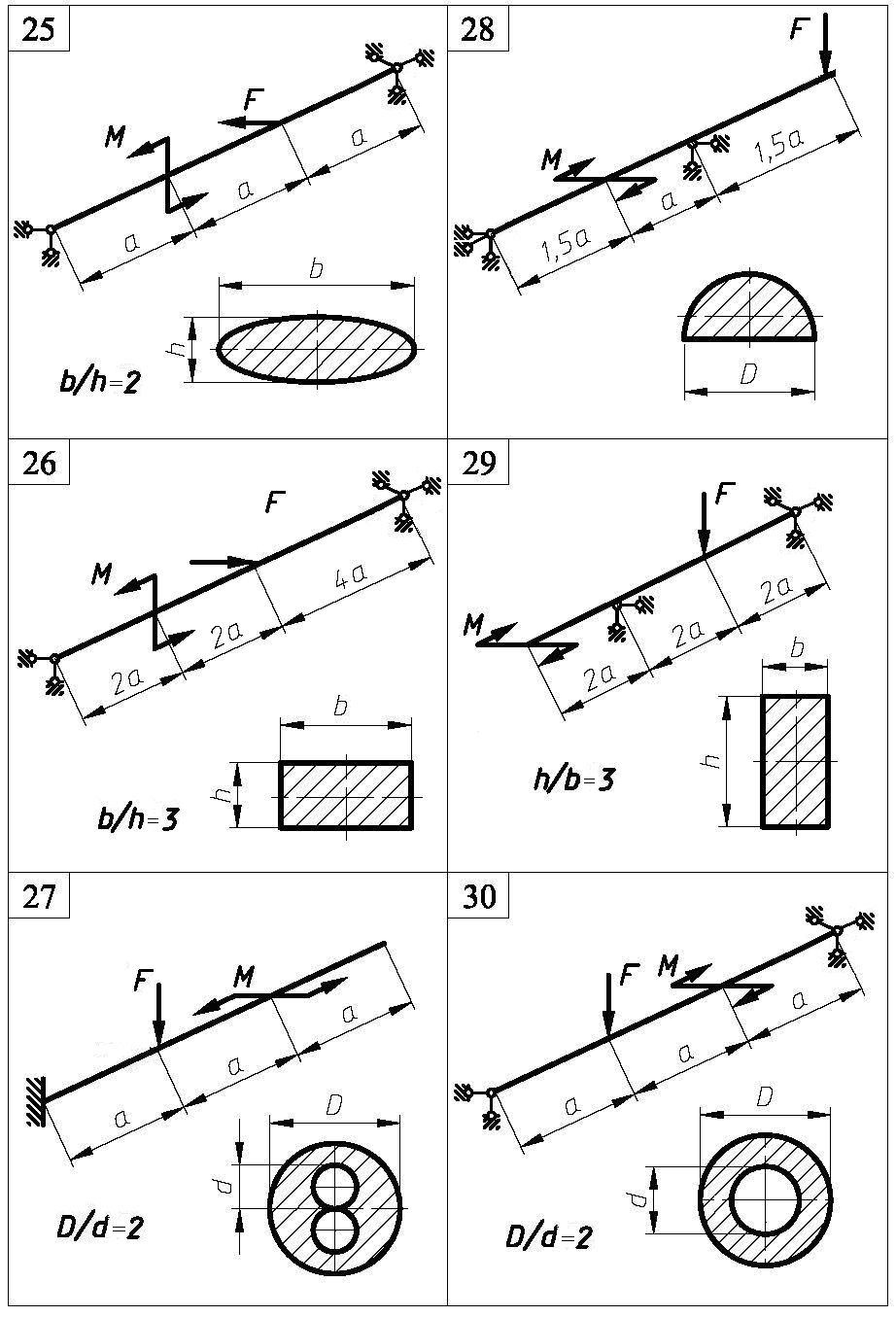
Рис.10. Закінчення

8. Накреслити на рисунку в аксонометрії балку з навантажен- ням, епюри згинальних моментів, які виникають у вертикальній та горизонтальній площинах, поперечний переріз балки в масштабі. На поперечному перерізі провести нейтральну лінію та побудувати епюру нормальних напружень.