3. Физический маятник

Физическим маятником называется любое тело, имеющее горизонтальную ось вращения, проходящую не через центр тяжести. Мы рассмотрим движение маятника, имеющего закрепленную ось подвеса О (рис. 4.2). Такой маятник совершает вращательное движение, поэтому уравнение колебаний получим из основного уравнения динамики вращательного движения:

.

Н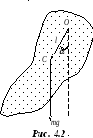а маятник действует сила тяжести , момент которой равен и направлен к нам. Моменты остальных сил (реакции) равны нулю. Припишем углу направление по правилу правого винта, т.е. навстречу моменту силы. Это справедливо для любого отклонения маятника, в чем легко убедится. Считаем направление углового ускорения положительным. Тогда угол будет отрицательным, а так как они направлены по одной прямой, можем переписать уравнение движения в скалярной форме для проекции на ось:

.

Угловое ускорение равно

,

где модуль угловой скорости.

Следовательно, уравнение гармонических колебаний физического маятника принимает вид . Ограничимся малыми углами, для которых (в радианах!). Отличие синуса от его аргумента для углов до 9⁰ не превышает 0,5%). Тогда получим

. (4.12)

Оно аналогично уравнению (4.5). Его решение подобно уравнению (4.6).

(4.13)

2. Попробуйте по аналогии с пружинным маятником, получить выражения для частоты и периода незатухающих собственных колебаний физического маятника, приведенные ниже.

Частота и период незатухающих колебаний физического маятника равны

.

Частным случаем физического маятника является математический маятник – материальная точка, подвешенная на нерастяжимой нити (рис. 4.3). Применяя к движению математического маятника основное уравнение динамики вращательного движения, все уравнения окажутся такими же, как для физического, только (момент инерции материальной точки относительно оси, проходящей через точку О перпендикулярно плоскости).

Уравнение колебаний математического маятника примет вид или , закон колебаний такого маятника имеет форму (4.13), причем .

Период гармонических колебаний математического маятника

.

3. Эта формула подтверждает четыре экспериментальных закона гармонических колебаний математического маятника устанавливающих, от каких параметров зависит или не зависит период колебаний такого маятника. Проанализируйте эту формулу и сформулируйте эти законы.

4. Колебательный контур

Рассмотрим идеальный (без сопротивления) колебательный контур с сосредоточенными параметрами – контур Томсона (рис. 4.4). присоединив к схеме источник постоянного напряжения (ключ в положении 1, рис. 4.5), зарядим конденсатор, затем перебросим ключ в положение 2, тем самым отсоединив источник и замкнув контур (рис. 4.6, а). Конденсатор начнет разряжаться через индуктивность, причем ток разрядки будет нарастать. На рисунке 4.7 изображен график зависимости силы тока в контуре от времени. Конденсатор разряжается не мгновенно, потому что катушка обл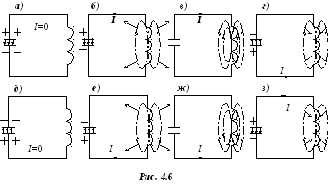 адает индуктивным сопротивлением, другими словами, при нарастании силы тока растет индукция магнитного поля, вызывающая э.д.с. и ток самоиндукции в контуре, направленные по правилу Ленца навстречу увеличению силы тока разрядки (0 – 1, рисунки 4.7 и 4.6, б; стрелками, перпендикулярными линиям индукции, показано направление «разворачивания» магнитного поля). Это направление силы тока (и магнитного поля) по мере уменьшения заряда на конденсаторе идет все медленнее и становиться равной нулю, когда конденсатор разрядится (рис. 4.6, в). Э.д.с. самоиндукции, мешающая току разрядки, уменьшается и достигает нуля в точке 1 (рис. 4.7), где сила тока максимальна. Магнитное поле начинает исчезать (см. рис. 4.6, г), уменьшается сила тока, но не мгновенно, так как при этом тоже возникает э.д.с. и ток самоиндукции в контуре, направленные по правилу Ленца навстречу уменьшению силы тока разрядки, т.е. в направлении тока разрядки (1 – 2, рис. 4.7). Катушка является источником тока и «гонит» электроны с одной незаряженной пластины на другую, перезаряжая конденсатор. Сила тока уменьшается, а скорость его уменьшения увеличивается, э.д.с. самоиндукции возрастает и достигает максимума при исчезновении тока (2, рис. 4.7).

При этом конденсатор оказывается перезаряженным, нет тока (см. рис. 4.6, д) и есть цепь разрядки. Конденсатор начинает разряжаться, э.д.с самоиндукции препятствует току разрядки, сила которого возрастает все медленнее (2 – 3, рис. 4.7). При этом магнитное поле разворачивается (см. рис. 4.6, е. сравните направления магнитных линий с направлениями аналогичных линий на рисунке 4.6, б. Э.д.с. самоиндукции уменьшается до нуля в точке 3 (рис. 4.7), где заряд конденсатора тоже равен нулю (см. рис. 4.6, ж). Сила тока начинает уменьшаться, возникает э.д.с. самоиндукции, препятствующая уменьшению силы тока, следовательно, поддерживающая ток в прежнем направлении. Катушка является источником тока, который перегоняет электроны с одной незаряженной пластины на другую, снова перезаряжая конденсатор (см. рис. 4.6, з). Сила тока уменьшается все быстрее, растут заряды на пластинах конденсатора и э.д.с. самоиндукции (все быстрее уменьшается магнитное поле).

В точке 4 (рис. 4.7) сила тока равна нулю, конденсатор вторично перезарядился (как на рис. 4.6, а), э.д.с. самоиндукции достигла максимума и начинает препятствовать новой разрядки конденсатора. Процесс повторяется, как от точки 0 (рис. 4.7).Мы качественно описали один период электрических колебаний – процесс изменения электрического и магнитного полей в колебательном контуре. Для количественного описания электрических колебаний нужно применить к колебательному контуру второе правило Кирхгофа:

.

Падение напряжения в произвольный момент времени равен напряжению на конденсаторе

.

Единственная э.д.с. в контуре – это э.д.с. самоиндукции

.

Следовательно,

.

Вспомним, что . Тогда , и уравнение гармонических колебаний заряда в колебательном контуре (электрических колебаний) примет вид или

. (4.16)

Оно похоже на уравнение (4.5). Его решение аналогично уравнению (4.6):

. (4.17)

Первая производная заряда – мгновенное значение силы тока

. (4.18)

Вторая производная заряда

.

Подставляя в уравнение колебаний выражения и , получаем

.

Снова ни , ни не равны нулю тождественно. Тогда, если

, (4.19)

выражение (4.17) обращает уравнение (4.16) в тождество, т.е. является законом гармонических колебаний заряда в томсоновском колебательном контуре.

Все величины и закономерности, установленные для гармонических колебаний в механике, сохраняют свой смысл и в электрических колебаниях. В частности, период таких колебаний не зависит от амплитуды заряда и равен

(4.20)

– формула Томсона.

Мы видим, что независимо от природы данного колебательного процесса и характера колеблющейся величины колебания совершаются одинаково, по одним и тем же законам, если системы подчиняются одинаковым закономерностям (несущественно, какая именно величина колеблется, важно, как она колеблется, какие колебания совершает).

4. Какие силы должны действовать в системе, способной совершать гармонические колебания, и какими свойствами должна она обладать?