Связь преобразований Фурье и Лапласа

Формула (1.3.7) прямого преобразования Лапласа может рассматриваться как результат определенным образом построенного обобщения одностороннего пре­образования Фурье. Пусть, например, функция удовлетворяет условиям Дирихле в интервале , причем при .

Преобразование Фурье может быть применено к функциям , для которых интеграл существует (условие абсолютной интегрируемости). Этому условию не удовлетворяют многие функции, используемые при анализе про­цессов в автоматических системах, например функции ; ; ; (при действительном ); t и др. Для того чтобы иметь возможность подобную функцию преобразовать по Фурье, предварительно её надо умножить на множитель , где вещест­венное число выбрано таким образом, чтобы интеграл

был сходящимся. Значение для каждой функции является вполне определенным. Используя формулу прямого одностороннего преобразования Фурье

будем преобразовывать по Фурье не функцию , а функцию , удовлетворяющую условиям применения этого преобразо­вания:

(1.3.13)

Введя новую комплексную переменную , получим:

Это выражение представляет собой формулу (1.3.7) прямого преобра­зования Лапласа.

Таким образом, преобразование Лапласа является результатом распространения преобразования Фурье на функции, которые, удов­летворяя условиям Дирихле в интервале , не удовлетво­ряют в этом интервале условию абсолютной интегрируемости.

Рассмотрим теперь формулу обратного преобразования Фурье

Заменив в левой и правой частях этого равенства на , получим

Учитывая, что , , найдем

Это равенство, как видно из (1.3.10), является формулой обратного преоб­разования Лапласа.

Таким образом, обратное преобразование Лапласа может рас­сматри­ваться как развитие обратного преобразования Фурье.

1.4 Прохождение регулярных сигналов через линейное звено

Любая часть системы автоматического управления может быть рассмотрена как некоторое звено системы, преобразующее сигнал входа в сигнал выхода. Если в качестве такого звена рас­сматривается объект регулирования, то входными сигналами являются управляющие воздействия и внешние возмущения, а выходными — регулируемые величины. При рассмотрении эле­ментарной системы регулирования как звена более сложной си­стемы управления входным сигналом будет сигнал уставки, а выходным — регулируемая величина.

Если преобразование сигнала может производиться звеном только в одном направлении, то звено называется звеном на­правленного действия. Как объект управления, так и элементар­ная система регулирования являются направленными звеньями, поскольку измене­ние регулируемой величины не оказывает обратного влияния на уставку и на внеш­ние воздействия.

Рассмотрим прохождение сигнала че­рез направленное звено (рисунок 1.4.1), в котором входной сигнал x преобразуется в выходной сигнал у. При регулярных сигналах x и y являются определенными функциями времени.

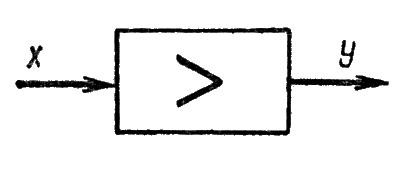
Рисунок 1.4.1 – Звено направленного действия

Дифференциальное уравнение, выражающее зависимость между x и у, определяет характеристики звена. Для линейных звеньев это дифференциальное уравнение линейное, и зависи­мость между x и у может быть выражена с помощью оператор­ной функции. Так как реальные системы в действительности нелинейны, т.е. описываются нелинейными дифференциальными уравнениями, то линейное их представление возможно только при гладких нелинейностях и малых изменениях x и у.