Разбиение по одному (комплексному) параметру

В некоторых случаях необходимо выяснить влияние какого-либо параметра на устойчивость системы. Предположим так же, как и при построении корневого годографа, что этот параметр входит линейно в характеристическое уравнение, которому можно придать вид

(2.3.2)

Границы D-разбиения согласно (2.3.1) определяются урав­нением

(2.3.3)

Отсюда

(2.3.4)

При построении границы D-разбиения достаточно построить ее для положительных значений ω () и затем до­полнить зеркальным отображением построенного участка отно­сительно действительной оси. Практически обычно интересует D-разбиение не всей комплекс­ной плоскости , а лишь её действительной оси, которой отве­чают действительные значе­ния .

На рисунке 2.3.2 показан вид границы D-разбиения в плос­кости . При измене­нии ω от до в плос­кости р мнимая ось проходит снизу вверх, при этом левая полуплоскось остается слева. Будем штриховать мнимую ось слева (рисунок 2.3.2, б). Такому движению по мнимой оси соот­ветствует движение по границе D-разбиения в плоскости (рисунок 2.3.2, а), которую будем также штриховать слева по обходу при изменении ω от до .

Если в плоскости пересекать границу D-разбиения по на­правлению штриховки (стрелка 1, рисунок 2.3.2, а), то в плоскости корней один корень переходит из правой полуплоскости в левую. Если же в плоскости пересекать границу D-разбиения против штриховки (стрелка 2, рисунок 2.3.2, а), то в плоскости корней один корень переходит из левой полуплоскости в правую.

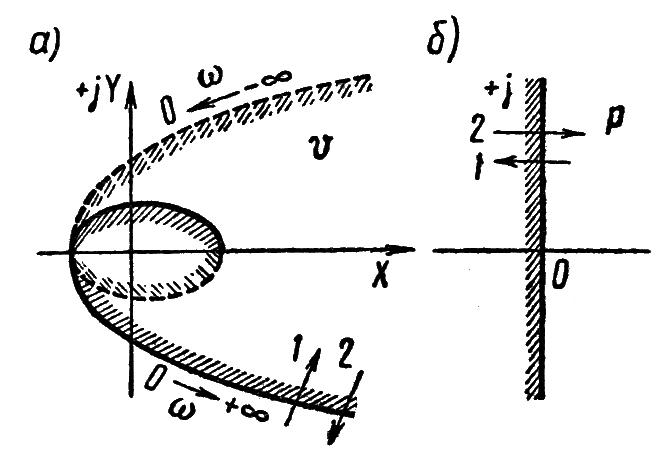
Рисунок 2.3.2 – Граница D-разбиения по одному параметру

Направление штриховки и число штриховок определяют на­правление перехода корней через мнимую ось и их число. По­этому для разметки областей достаточно знать распреде­ление корней относительно мнимой оси при каком-либо произ­вольном значении параметра. Переходя в плоскости от этого значения параметра к любому другому, по числу пересечений границы D-разбиения и направлению штриховки, можно определить значение m в любой точке. Областью устойчивости будет область и претендентом на эту область (отрезок) — область (отрезок), к которой направлена штри­ховка.

Обычно в линейных задачах изменяемый параметр является вещественным (коэффициент усиления, постоянная времени) и практический интерес имеет область D-разбиения, прилегаю­щая к оси X. Рассмотрение всей области комплексного пара­метра представляет интерес для нелинейных задач, где может быть использован полученный результат.

D-разбиение по двум параметрам

В ряде случаев необходимо выяснить влияние на устойчи­вость системы не одного параметра, а двух. Предположим, что эти параметры линейно входят в характеристическое уравнение и ему можно придать вид

(2.3.5)

где , , — полиномы от p; τ и ν — варьируемые параметры.

Граница D-разбиения в плоскости τ и ν согласно (2.3.1) определяется уравнением

(2.3.6)

Обозначим

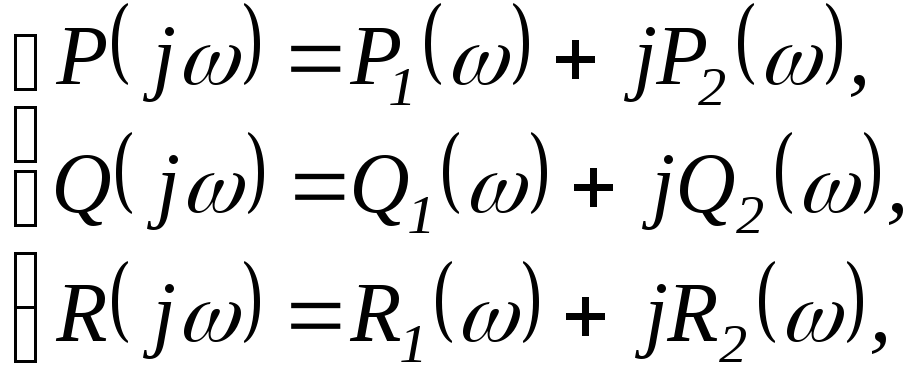(2.3.7)

тогда уравнение (2.3.6) можно разбить на два уравнения, при­равняв раздельно вещественную и мнимую части нулю:

(2.3.8)

(2.3.9)

Решая систему уравнений (2.3.8) и (2.3.9) относительно τ и ν, получим

(2.3.10)

(2.3.11)

где

(2.3.12)

(2.3.13)

(2.3.14)

При для каждого значения ω по уравнениям (2.3.10)–(2.3.14) можно определить величины τ и ν и, таким образом, в пло­скости τ и ν построить границу D-разбиения.

Из (2.3.10)–(2.3.14) видно, что , и являются нечётными функциями ω, ибо вещественные части , и — чётные функции ω, а мнимые — нечётные функции. Отсюда следует согласно (2.3.10) и (2.3.11), что τ и ν являются чётными функциями ω.

Рассмотрим случай, когда при некотором значении ω опре­делитель равен нулю (). Тогда, если при этом значе­нии ω определители и не равны нулю, то точка границы D-разбиения в плоскости τ и ν уходит в бесконечность. Если же при этом значении ω определители и также будут равны нулю, то τ и ν согласно (2.3.10) и (2.3.11) будут неопре­делёнными. Это соответствует тому, что уравнения (2.3.8) и (2.3.9) становятся эквивалентными и определяют собой прямую в пло­скости τ и ν, т.е. для рассматриваемого значения ω (при котором ) получим в плоскости τ и ν не точку, а прямую, называемую особой прямой.

В большинстве практических задач особые прямые отвечают значению и . В этом случае коэффициенты, соответствующие свободному и старшему членам характеристиче­ского уравнения, зависят от τ и ν, и для получения уравнений этих особых прямых необходимо указанные коэффициенты приравнять нулю. Первый коэффициент (свободный член) дает прямую для , второй — для .

Рассмотренное выше решение системы уравнений (2.3.8) и (2.3.9) может быть проведено графически. На рисунке 2.3.3 показаны прямые 1 и 2 для заданного значения ω, соответствующие уравнениям (2.3.8) и (2.3.9) для трёх случаев:

1. и ,

2. и ,

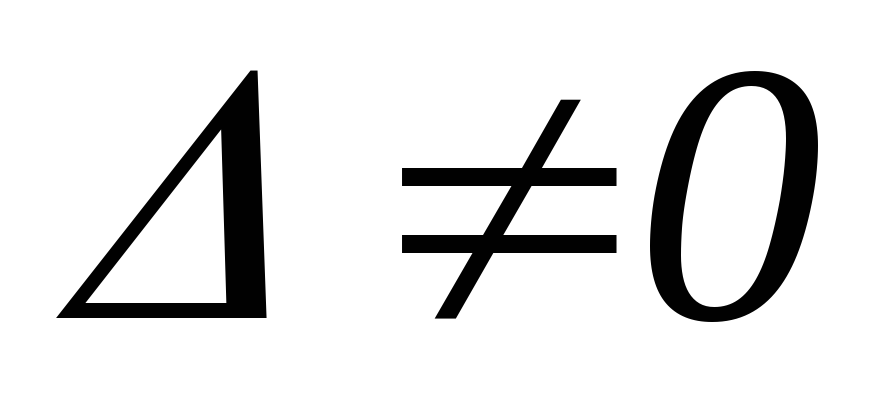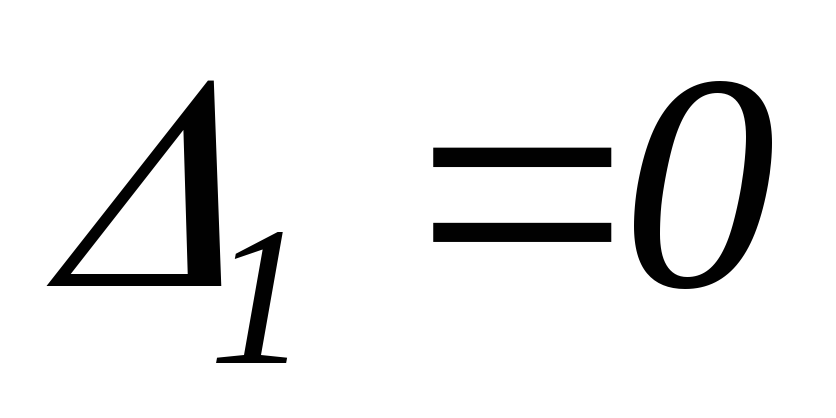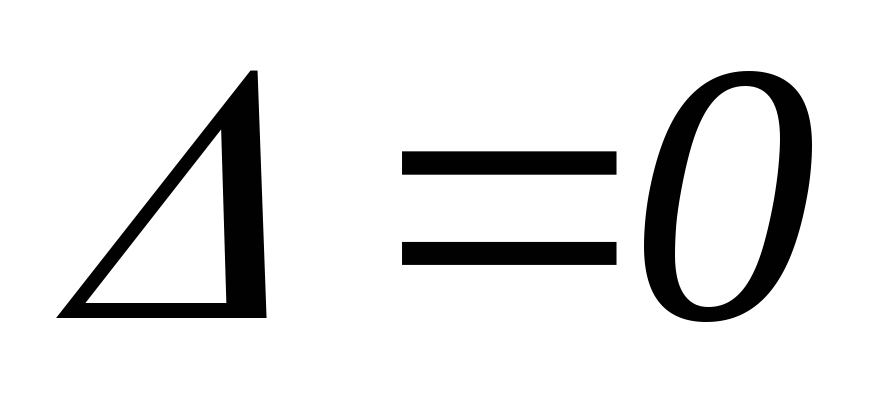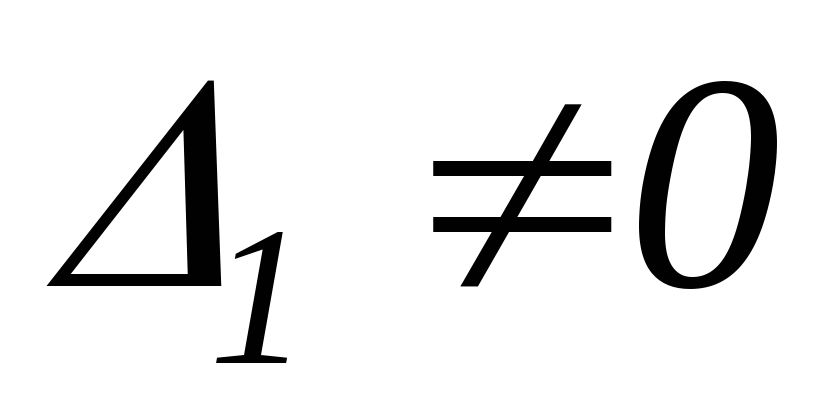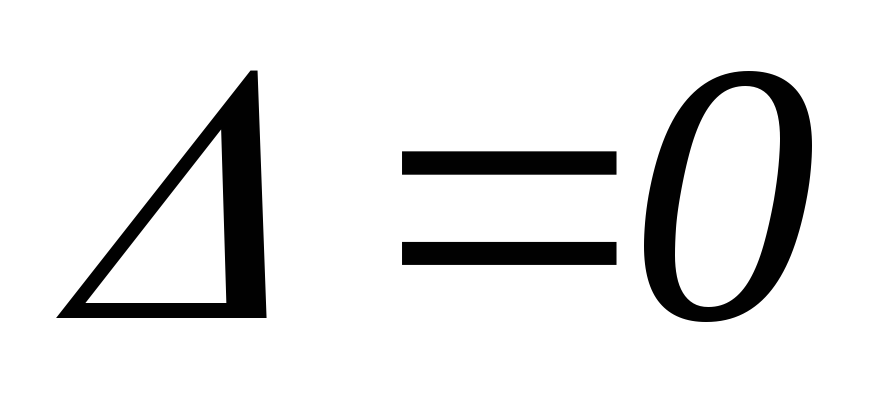3. и .

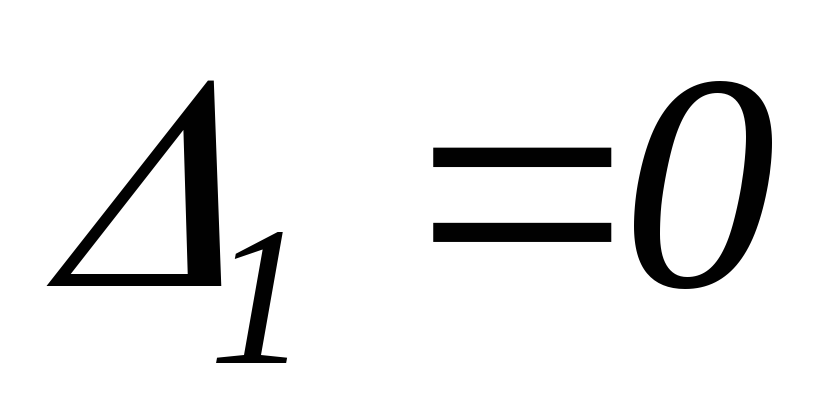В первом случае точка пересечения прямых 1 и 2 опреде­ляет значения τ и ν для заданного значения ω; во втором случае прямые 1 и 2 параллельны и определяют значения τ и ν, равные бесконечности; в третьем случае прямые 1 и 2 слива­ются друг с другом, и, таким образом, для заданного значе­ния ω получается прямая, а не одна точка.

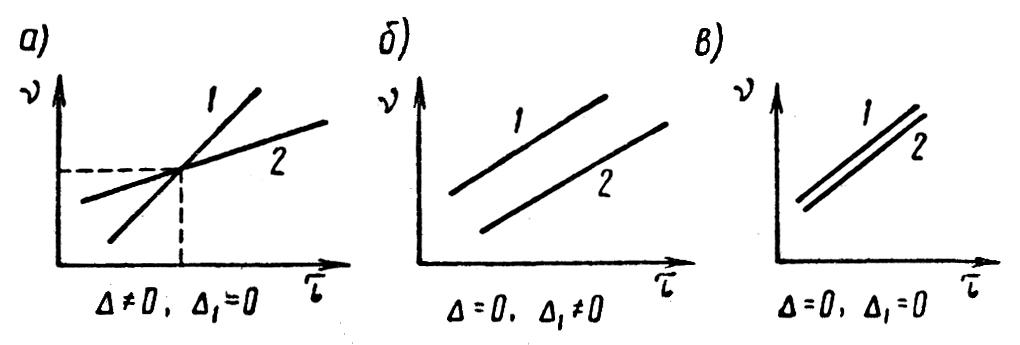
Рисунок 2.3.3 – Особые прямые

Правила штриховки границы D-разбиения. Граница D-разбиения штрихуется слева при обходе в сторону возрастающих ω, если главный определитель , и справа, если . Так как граница D-разбиения для положительных и отрицательных значений ω совпадает (величины τ и ν — чёт­ные функции ω, а — нечётная функция), то она штрихуется дважды с одной и той же стороны (рисунок 2.3.4).

При всегда , и через точку, соответствующую (и ), чаще всего, как указывалось, проходят особые прямые. Штриховка этих особых прямых ординарная и производится так, чтобы вблизи точки сопряжения прямой и кривой заштрихованные и незаштрихованные стороны прямой и кривой были направлены друг к другу (рисунок 2.3.4, а, б, в).

В тех случаях, когда при , а проходит через нуль и меняет знак (это сравнительно редкий случай), появ­ляется особая прямая; она штрихуется в этом случае по сформулированному выше правилу, но двойной штриховкой (рисунок 2.3.4, г).

Если же при , а проходя через нуль, не меняет знака, то особая прямая не штрихуется и выбрасывается из рассмотрения (рисунок 2.3.4, д).

При построении границы D-разбиения по двум параметрам следует правильно ориентировать оси. Для проведенной выше записи уравнений τ следует откладывать по оси абсцисс, ν — по оси ординат. В случае перемены местами осей τ и ν соответственно изменяется ориентация штриховки относительно правой и левой сторон.

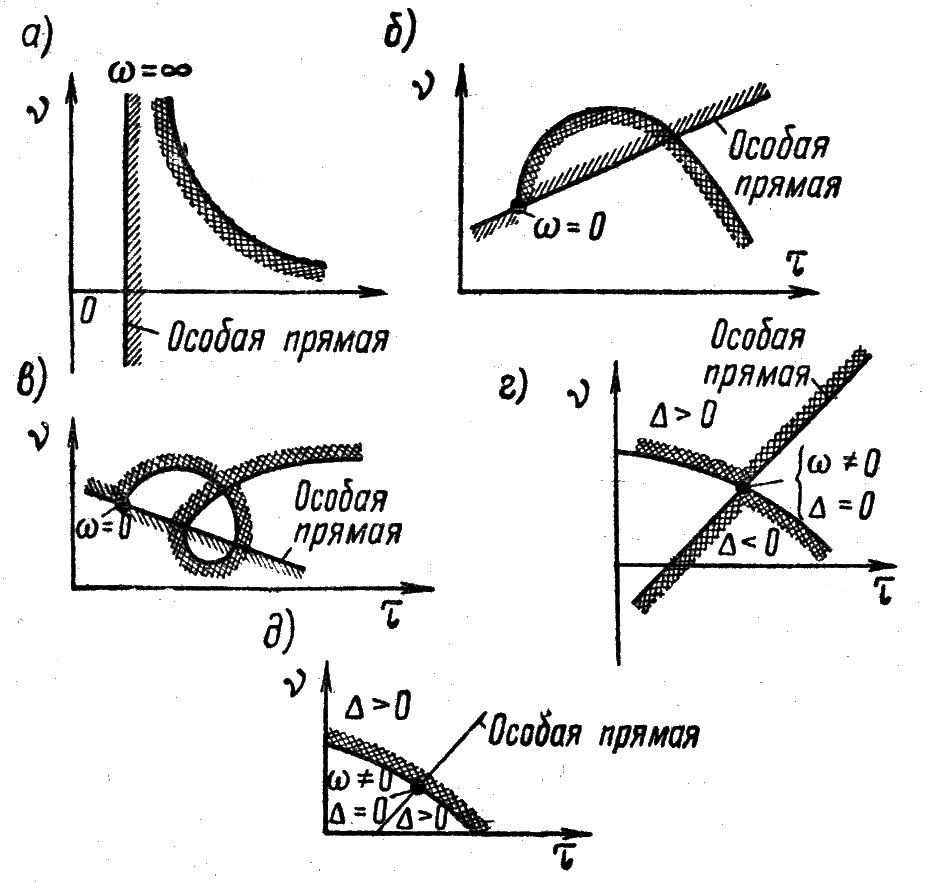
Рисунок 2.3.4 – Штриховка границы D-разбиения