
- •Раздел 1. Основные понятия теории автоматического управления. Типовые звенья линейных систем автоматического управления. Соединение линейных звеньев
- •1.1 Основные принципы и понятия автоматического управления
- •1.2 Примеры систем автоматического управления
- •1.3 Основные понятия операционного исчисления. Преобразование Фурье и Лапласа
- •Связь преобразований Фурье и Лапласа
- •1.4 Прохождение регулярных сигналов через линейное звено
- •Регулярные сигналы
- •1.5 Характеристики линейного звена
- •1.6 Устойчивость линейных звеньев. Минимально-фазовые звенья. Преобразование произвольного сигнала линейным звеном
- •1.7 Типовые динамические звенья. Простейшие звенья. Звенья первого порядка
- •Простейшие звенья
- •Звенья первого порядка
- •1.8 Колебательные звенья. Особые звенья: неминимально-фазовые устойчивые звенья, неустойчивые звенья
- •Устойчивые неминимально-фазовые звенья
- •Неустойчивые звенья
- •1.9 Особые звенья: иррациональные и трансцендентные звенья Иррациональные звенья
- •Трансцендентные звенья
- •1.8 Соединение линейных звеньев. Преобразование структурных схем
- •Последовательное соединение звеньев
- •Параллельное согласное соединение звеньев
- •Параллельное встречное соединение звеньев
- •Преобразование структурных схем
- •Раздел 2. Исследование устойчивости линейных систем автоматического управления. Качество процессов управления
- •2.1 Постановка задачи исследования устойчивости линейных систем автоматического управления. Алгебраические критерии устойчивости. Критерий Рауса, критерий Гурвица
- •Алгебраические критерии устойчивости
- •2.2 Частотные критерии устойчивости. Критерий Михайлова. Критерий Найквиста
- •2.3 Влияние параметров системы на её устойчивость. Метод d-разбиения
- •Разбиение по одному (комплексному) параметру
- •2.4 Показатели качества процессов управления
- •2.5 Качество регулирования при стандартных воздействиях
- •2.6 Косвенные методы исследования качества процессов управления. Интегральные оценки качества переходных процессов
Параллельное встречное соединение звеньев
Параллельным встречным соединением двух звеньев называется такое соединение, при котором выходной сигнал первого звена подается на вход второго, а выходной сигнал второго звена с соответствующим знаком суммируется с общим входным сигналом и подается на вход первого звена. Общим выходным сигналом является выход первого звена (см. рисунок 1.8.3).
Звено, в котором направление передачи сигнала совпадает с направлением передачи общего сигнала (первое звено), называется звеном прямой связи, а звено, в котором направление передачи сигнала противоположно направлению передачи общего сигнала (второе звено), называется звеном обратной связи. Если знак сигнала обратной связи положителен, т.е. если он суммируется с общим сигналом (см. рисунок 1.8.3, а), то обратная связь называется положительной. Если знак сигнала обратной связи отрицателен, т.е. если он вычитается из общего сигнала (см. рисунок 1.8.3, б), то обратная связь называется отрицательной.

Рисунок 1.8.3 – Параллельное встречное соединение звеньев
Параллельное встречное соединение представляет собой такое сочетание последовательного и параллельного соединения, при котором звенья прямой и обратной связи соединены между собой последовательно в виде замкнутого кольца, а внешний сигнал подается параллельно к общей точке первого и второго звена. Уравнения параллельного встречного соединения имеют вид:
1) уравнения входа:
а) для положительной обратной связи
![]() (1.8.10)
(1.8.10)
б) для отрицательной обратной связи
![]() (1.8.11)
(1.8.11)
Эти уравнения называются уравнениями замыкания;
2) уравнение выхода
![]() (1.8.12)
(1.8.12)
В теории регулирования и управления большей частью рассматривают цепи с отрицательной обратной связью и пользуются уравнением (1.8.11). Рассматривая совместно уравнения (1.8.11) и (1.8.12) и имея в виду, что
![]()
![]()
![]()
получаем
![]()
откуда
![]() (1.8.13)
(1.8.13)
или
![]() (1.8.14)
(1.8.14)
Для звеньев с дробно-рациональной передаточной функцией
![]()
и
![]()
уравнение (1.8.14) может быть записано как
![]() (1.8.15)
(1.8.15)
Из рассмотрения
этого уравнения можно сделать вывод,
что нули
![]() совпадают с нулями
совпадают с нулями
![]() и полюсами
и полюсами
![]() ,
однако полюсы функции
,
однако полюсы функции
![]() отличаются от полюсов
отличаются от полюсов
![]() и
и
![]() .
Таким образом, устойчивые звенья при
параллельном встречном соединении
могут образовать неустойчивую систему.
Наоборот, соединение звеньев, среди
которых имеются неустойчивые, может
оказаться устойчивым. При гармонических
сигналах комплексный коэффициент
усиления
.
Таким образом, устойчивые звенья при
параллельном встречном соединении
могут образовать неустойчивую систему.
Наоборот, соединение звеньев, среди
которых имеются неустойчивые, может
оказаться устойчивым. При гармонических
сигналах комплексный коэффициент
усиления
![]() (1.8.16)
(1.8.16)
Если цепь обратной
связи представляет собой пропорциональное
звено
![]() ,
то обратная связь называется жёсткой,
или пропорциональной.
,
то обратная связь называется жёсткой,
или пропорциональной.
Если цепь обратной
связи представляет собой дифференцирующее
звено
![]() или
или
![]() ,
то обратная связь называется гибкой,
или дифференцирующей.
,
то обратная связь называется гибкой,
или дифференцирующей.
Если цепь обратной
связи представляет собой интегрирующее
звено
![]() ,
то обратная связь называется
интегрирующей.
,
то обратная связь называется
интегрирующей.
Преобразование структурных схем
Рассмотрим три элемента структурной схемы: узел разветвления, суммирующий узел и звено, преобразующее сигнал.
Для различных схем соединения введем понятие направления ветвления, указывающее направление разделения сигнала на составляющие или направление его передачи по нескольким ветвям (разветвления). Направление ветвления может или соответствовать, или быть противоположным направлению передачи сигнала. В суммирующем узле направление ветвления противоположно направлению передачи сигнала, а в узле разветвления — совпадает с направлением передачи сигнала. На рисунке 1.8.4 показаны узел разветвления (а) и суммирующий узел (б), двумя различными стрелками показаны направление передачи сигнала (зачернённая стрелка) и направление ветвления (незачернённая стрелка).
Направление ветвления является понятием, применимым как при передаче сигналов, так и при передаче вещества. Наглядным примером рассмотрения направления ветвления при передаче вещества может служить обтекание потоком жидкости тела с двух сторон (рисунок 1.8.4, в). Здесь направление ветвления выше обтекаемого тела (область 1) направлено по течению жидкости, а ниже обтекаемого тела (область 2) — против течения жидкости.

Рисунок 1.8.4 – Примеры разветвлений
Рассмотрим два вида преобразования схем:
а) перемещение суммирующего узла через узел разветвления;
б) перемещение звена через узел.
Правила преобразования схем при каждом из этих видов перемещения существенно зависят от, того, совпадает ли направление перемещения с направлением ветвления или они противоположны.
Перемещение суммирующего узла через узел разветвления. Пусть направление перемещения суммирующего узла совпадает с направлением ветвления (рисунок 1.8.5, а). Тогда перемещение суммирующего узла за узел разветвления изменит сигнал в узле разветвления и, следовательно, изменит сигнал во всех остальных ветвях, отходящих от узла. Для того чтобы скомпенсировать это изменение, необходимо в отходящей ветви добавить такой же суммирующий узел, как и перемещаемый узел (рисунок 1.8.5, б).
Условие эквивалентности схем, показанных на рисунке 1.8.5 (а) и (б), определяется уравнением
![]() (1.8.17)
(1.8.17)
справедливым для обеих схем.
Таким образом, можно сформулировать первое правило преобразования. При перемещении суммирующего узла через узел разветвления по направлению ветвления необходимо в отходящих от разветвления ветвях добавить такие же, как и перемещаемый узел, суммирующие узлы (рисунок 1.8.5, а и б).

Рисунок 1.8.5 – Перемещение суммирующего узла через узел разветвления
Если направление перемещения суммирующего узла противоположно направлению ветвления (рисунок 1.8.5, в), то условия преобразования несколько изменяются. В этом случае для компенсации влияния переноса узла необходимо не добавлять к ответвляемым величинам слагаемые в узле, а вычитать их (рисунок 1.8.5, г).
При этом для эквивалентности схем (в) и (г) и сохранения значений величин, подводимых к схеме и отводимых от нее, необходимо, чтобы от величины, отводимой от узла разветвления, отнималась такая же величина (x2), как и та, которая была добавлена в перенесенном суммирующем узле.
Второе правило преобразования (для этого случая) формулируется следующим образом. При перемещении суммирующего узла через узел разветвления против направления ветвления необходимо в отходящих от разветвления ветвях добавить суммирующие узлы, отличающиеся от перемещаемого знаками прибавляемых величин (рисунок 1.8.5, в и г).
Перемещение звена через узел. При перемещении звена через узел также определяющее значение имеет направление ветвления. Рассмотрим перемещение звена по направлению ветвления. Если перемещение звена W1 производится через узел разветвления величины y1 (рисунок 1.8.6, а), то условием сохранения значений величин, отводимых от схемы, является выполнение условия
![]() (1.8.18)
(1.8.18)
Очевидно, что для соблюдения этого условия необходимо во всех отходящих от узла ветвях добавить звено с передаточной функцией W1. Из рассмотрения схем (а) и (б), показанных на рисунке 1.8.6, видно, что они эквивалентны по отношению к внешним соединениям.
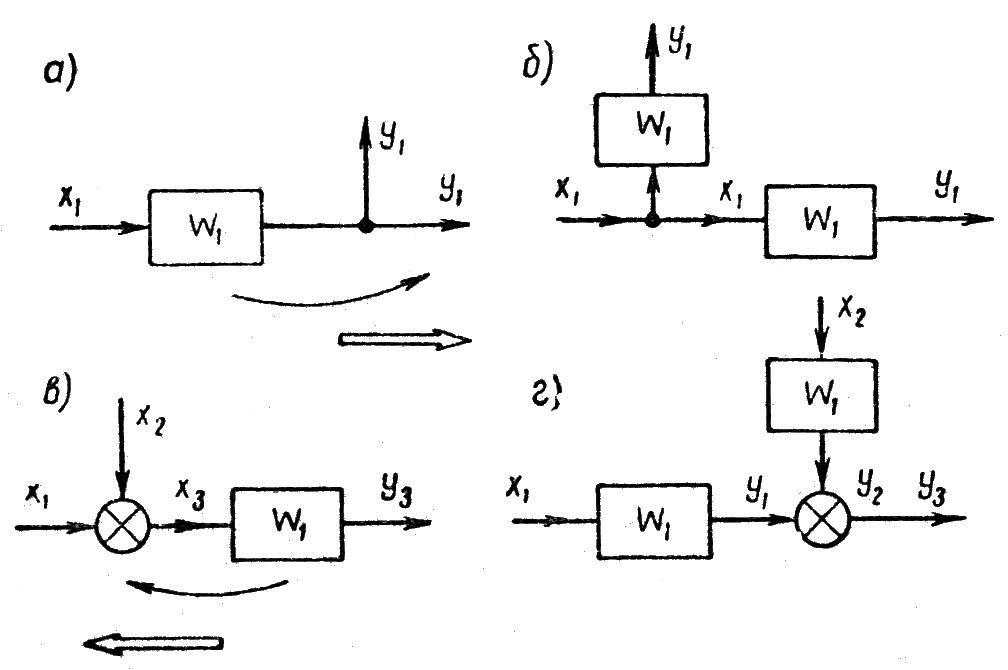
Рисунок 1.8.6 – Перемещение звена через узел по направлению ветвления
Если перемещение звена производится через суммирующий узел по направлению ветвления, то можно прийти к аналогичным выводам. В этом случае уравнение
![]() (1.8.19)
(1.8.19)
выполняется, если во всех ветвях, отходящих от узла, добавляются звенья с передаточной функцией W1. Условие эквивалентности таких схем иллюстрируется схемами (в) и (г), показанными на рисунке 1.8.6.
Третье правило преобразования формулируется так. При перемещении звена через узел по направлению ветвления необходимо в подсоединенные к узлу ветви добавить звенья с передаточной функцией перемещаемого звена (рисунок 1.8.6).
Если направление перемещения звена противоположно направлению ветвления, то условия преобразования изменяются. В этом случае для компенсации влияния звена, перенесенного в общую ветвь (на сигналы в отходящих от узла ветвях), необходимо в эти ветви включить звенья с обратными передаточными функциями.
Условие эквивалентности вытекает из уравнения (1.8.18) для перемещения звена через узел разветвления (рисунок 1.8.7, а и б) и из уравнения (1.8.19) для перемещения звена через суммирующий узел (рисунок 1.8.7, в и г).

Рисунок 1.8.7 – Перемещение звена через узел против направления ветвления
Четвертое правило преобразования может быть сформулировано так. При перемещении звена через узел против направления ветвления необходимо в подсоединенные к узлу ветви добавить звенья с передаточной функцией, обратной передаточной функции перемещаемого звена (см. рисунок 1.8.7).
Применение четырех приведенных правил дает возможность производить самые различные преобразования структурных схем. При этом следует иметь в виду, что перемещение звена или узла из одной ветви в другую может производиться только при согласных направлениях передачи сигнала в этих ветвях.
