4. Числовые характеристики случайных величин

Числовые характеристики случайных величин широко применяют на практике. При этом зачастую нет необходимости полностью, исчерпывающим образом характеризовать случайную величину. Достаточно бывает указать числовые параметры, которые характеризуют существенные черты распределения случайной величины:

1) среднее значение, около которого группируются возможные значения случайной величины;

2) число, характеризующее рассеяние случайной величины относительно среднего значения и т.д.

Числовые параметры, позволяющие в сжатой форме выразить наиболее существенные особенности случайной величины, называются числовыми характеристиками случайной величины.

4.1. Математическое ожидание

Математическое ожидание (среднее значение) непрерывной случайной величины Х, возможные значения которой принадлежат интервалу (a,b), представляет собой определенный интеграл

X_ср.=<X>=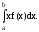 (22)

Математическое ожидание можно выразить через дополнение интегральной функции. Для этого в формулу (22) подставляем формулу (13) для определения дополнения интегральной функции и проинтегрируем по частям:

<X>=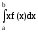==-=-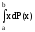xP(x)+=

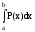=-b P(b)+a P(a)+=a+.

Так как P(b)=0, P(a)=1, то

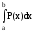X_ср.=<X>==a+. (23)

Для неотрицательных случайных величин, возможные значе-

Т а б л и ц а 1

Ряд распределения случайной величины

Значения случайной

величины Х₁ Х₂ ... ... Х_n

Вероятность

Р(Х=Х_i)=Р Р₁ Р₂ ... ... Р_n

При графическом представлении по оси абсцисс откладываются значения случайной величины, по оси ординат - вероятности Р_i , соответствующие этим значениям.

Рис. 2. Многоугольник распределения случайной величины

Ряд распределения удобен, когда закон распределения дискретной случайной величины имеет конечное число значений. В случае непрерывной случайной величины, имеющей бесчисленное множество значений, такая форма закона неприемлема. В этом случае используют не вероятность события Р_i(x=x_i), а вероятность P(Xx_i). Следовательно, случайная величина X примет значение, меньшее какого-либо наперед заданного (-x).

Наиболее универсальной характеристикой как дискретных (прерывных), так и непрерывных случайных величин является функция или интегральный закон распределения случайной величины.

Пусть X - случайная величина и x - некоторое действительное число, тогда вероятность того, что Xx

F(x)=P(Xx),

где F(x) - функция распределения.

Эту функцию можно представить в виде графика , где по оси абсцисс отложены значения х, а по оси ординат - значения F(х). График функции непрерывной случайной величины - плавная кривая при любом значении (рис. 3).

Если Х - дискретная величина, то на основании теоремы сложения вероятностей несовместных событий

F(x)=.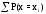

В этом случае график имеет ступенчатый вид (рис. 4). С увеличением числа значений x число ступеней будет увеличиваться, а их величина - уменьшаться.

Рис. 3. График функции непре- Рис. 4. График функции диск-

рывной случайной величины ретной случайной величины

Из графиков видно, что функция распределения изменяется в пределах

0F(x)1.