3.2.1. Частота появления событий

Частота появления событий - это вероятность их появления в единицу времени.

Непрерывные случайные величины в теории надежности связаны с событиями, в результате которых случайная величина принимает то или иное случайное значение.

Дифференциальная функция (плотность распределения) может быть представлена как частота появления событий (например, частота отказов объектов, частота восстановления объектов).

Частота отказов по статистической информации определяется как отношение числа объектов, отказавших в единицу времени, к числу объектов в начале испытания:

f*(t)==,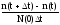

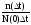где t - интервал времени от t до t+t; n(t) - число объектов, отказавших в интервале времени t; n(t) - число объектов, отказавших за время t; N(0) - число объектов в начале испытания, N(0)=N(t)+n(t).

3.2.2. График дифференциальной функции распределения вероятностей случайной величины

График дифференциальной функции, построенный по статистической информации, называют гистограммой.

Для построения гистограммы разбивают весь диапазон возможных значений непрерывной случайной величины на интервалы t, обычно равной длины, и для каждого интервала определяют частоту появления событий f*(t) и откладывают по оси ординат. В результате получают прибли-

Рис. 10. График дифференциальной женное представле-

функции распределения ние кривой диффе-

ренциальной функ-

ции распределения вероятностей в виде ступенчатой линии (рис. 10). Площади столбцов приближенно равны соответствующим площадям криволинейных трапеций под кривой дифференциальной функции.

Для более точного приближения необходимо, чтобы в каждый интервал попало достаточное множество эмпирических точек.

3.2.3. Вероятность попадания непрерывной случайной величины в заданный интервал

Вероятность попадания непрерывной случайной величины в заданный интервал (a,b), выраженная через дифференциальную функцию, определяется интегральным уравнением выражения (11) в пределах от a до b с учетом формулы (9):

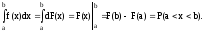(14)

То есть вероятность попадания непрерывной случайной величины х в заданный интервал (a,b) равна определенному интегралу от дифференциальной функции в пределах от a до b.

Геометрически вероятность попадания непрерывной случайной величины х в интервал (a,b) равна площади криволинейной трапеции, ограниченной осью абсцисс, графиком дифференциальной функции f(x) и прямыми x=a и x=b (рис. 11).

Вероятность появления случайного события (отказа объекта, восстановления работоспособности объекта) на интервале (a,b) равна вероятности попадания соответствующей ему слу-

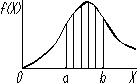
чай ной величины Т (вре-

мени безотказной работы Рис. 12. Вероятность попадания не-

объекта, времени восста- прерывной случайной величины

новления работоспособ-

ности объекта) в этот интервал.

3.2.4. Свойства дифференциальной функции распределения

1. Дифференциальная функция неотрицательна, f(x)0, так как производная неубывающей функции неотрицательна.

2. Интеграл от дифференциальной функции в пределах области существования всех возможных значений случайной величины от a до b равен единице:

(15)

Интеграл (15) от дифференциальной функции выражает вероятность события, состоящего в том, что случайная величина принимает значение, принадлежащее интервалу (a,b), в котором заключены все ее возможные значения. Такое событие достоверно, и его вероятность равна единице. Геометрически это означает, что вся площадь криволинейной трапеции, ограниченной осью х и графиком дифференциальной функции (кривой распределения), равна единице.