2.2. Теоремы теории вероятностей

1. Формула сложения вероятностей. Если при испытаниях может произойти только одно из рассматриваемых событий A₁, A₂,...,A_n, а вместе они появиться не могут, то эти события несовместные. Рассматриваемое сложное событие А называют суммой исходных событий:

A=A₁+A₂+...+A_n=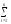A_i.

Если вероятности событий подчиняются таким же соотношениям, как и соответствующие им частости, то получим теорему (формулу) сложения вероятностей:

P(A)=P(A₁+A₂+...+A_n)=P(A₁)+P(A₂)+...+P(A_n)= 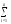P(A_i).

B общем случае для полной группы несовместных событий

P(A_n)=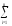P(A_i)=1. (2)

Полная группа событий - события, когда в результате испытаний обязательно наступит хотя бы одно из них. Например, при длительных испытаниях механического оборудования обязательно появится отказ.

Для двух несовместных событий A и 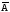, образовавших полную группу,

P(A)=1-P(). (3)

Например, в надежности чаще рассматриваются два несовместных противоположных события - состояние работоспособности и отказ. Они составляют полную группу.

Для двух совместных событий A₁ и A₂, образовавших полную группу,

P(A₁+A₂)=P(A₁)+P(A₂)-P(A₁A₂). (4)

2. Формула умножения вероятностей. Если события независимы, то появление одного из них не изменяет вероятности появления другого:

P(AB)=P(A)P(B). (5)

Для двух зависимых событий

P(A)=P(B)P(AB)=P(A)². (6)

Сложное событие A, заключающееся в одновременном осуществлении нескольких событий, называется произведением исходных событий A_i:

A=A₁A₂...A_n=.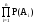

Вероятность независимых событий по теореме умножения вероятностей

P(A)=P(A₁,A₂,...,A_n)=P(A₁)P(A₂)...P(A_n)=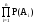. (7)

Если

P(A₁)P(A₂)=...=P(A)=P,

то

=.

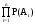2.3. Законы распределения случайной величины

Законы распределения случайной величины - это соотношения, устанавливающие связь между возможными значениями случайных величин и соответствующими значениями вероятностей или частот (частостей). Закон распределения случайной величины позволяет определить вероятность (частоту, частость) появления случайной величины в любом интервале ее возможных значений.

Дискретные случайные величины Х могут принимать только ряд отдельных значений х₁,х₂,...,х_n; каждому значению соответствует определенное значение вероятностей Р₁,Р₂,...,Р_n. Эти события образуют полную группу несовместных случайных событий, для которых

Р₁+Р₂+...+Р_n=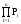=1.

Распределение прерывной случайной величины может быть представлено в виде таблицы (табл. 1), называемой рядом распределения, или графически (рис. 2) - многоугольника распределения.

(ЭНО), то есть модель испытания объектов на долговечность, применяют для определения вероятностных характеристик ресурса и срока службы объектов, а также наработки до первого отказа.

Статистическую информацию об отказах получаем при наблюдениях за эксплуатацией или испытаниями при определенных условиях N одинаковых объектов. При этом каждый объект работает от начала эксплуатации до первого отказа, не восстанавливается и не заменяется новым (работоспособным). Испытания заканчивают после отказа всех объектов. Наработка каждого объекта до первого отказа записывается в виде вариационного ряда

t₁t₂...t_i...t_N.

Закон распределения случайной величины является ее универсальной вероятностной характеристикой.

В модели ЭНО случайным событием является отказ объекта, а случайной величиной - ресурс, то есть наработка объекта от начала эксплуатации до перехода в предельное состояние. Случайные события будут полностью описаны с вероятностной точки зрения, если задать распределение вероятностей соответствующих им случайных величин.

Законом распределения вероятностей называют соотношения, устанавливающие связь между возможными значениями случайной величины и соответствующими им вероятностями. Этот закон имеет разные формы:

1) ряд распределения;

2) интегральная функция распределения;

3) дифференциальная функция распределения.