9.1.6. Простейший поток событий

Среди потоков событий простейший поток играет особую роль. Он обладает свойствами стационарности, отсутствия последействия и ординарности.

Суммирование (взаимное наложение) большого числа независимых стационарных, ординарных потоков с любым последействием дает поток, близкий к простейшему. Но при этом должны соблюдаться условия, аналогичные центральной предельной теореме: каждое слагаемое должно оказывать на сумму сравнительно малое влияние.

Поток отказов восстанавливаемых объектов в период нормальной эксплуатации при неизменных условиях оказывается простейшим, с постоянным значением его интенсивности, т.е. параметра потоков отказов. Поток восстановлений работоспособности объектов на практике - простейший поток.

9.1.7. Математическая модель простейшего потока событий

Математическая модель простейшего потока событий должна отражать все три его свойства:

- стационарность,

- отсутствие последействия,

- ординарность.

Вероятность появления n событий простейшего потока за время t при известной интенсивности  определяется по формуле Пуассона:

P_n(t)== 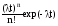(n=0,1,2,...), (62)

где H - среднее число событий.

Эта формула отражает все три свойства простейшего потока, поэтому она является математической моделью потока.

Экспоненциальное распределение длительности интервала времени между соседними событиями простейшего потока является следствием: 1) стационарности, 2) отсутствия последействия, 3) ординарности.

Рассмотрим случайную величину T - это длительность интервала времени между двумя произвольными соседними событиями в простейшем потоке, и найдем ее функцию распределения

F(t)=P(T<t).

Вероятность противоположного события (T>t)

P(t)=1-F(t)=P(T>t),

т.е. вероятность того, что на интервале времени длительностью t, начинающимся в момент t_k появления одного из событий потока, не появится ни одно из последующих событий, т.к. простейший поток не обладает последействием. Поэтому вероятность P(t)=P(T>t) вычисляется по формуле Пуассона (62) при n=0:

P(t)=P(T>0)==exp(-t). (63)

Интегральная функция распределения

F(t)=P(T<t)=1-exp(-t). (64)

Дифференциальная функция (плотность вероятностей) определяется дифференцированием формулы (64):

f(t)= exp(-t).

Среднее время между соседними событиями простейшего потока

T_cp=, (65)

т.е. равно величине, обратной интенсивности потока событий.

Экспоненциальное распределение времени безотказной работы объекта в период нормальной эксплуатации является следствием того, что поток отказов становится простейшим, т.к. обладает свойствами стационарности, отсутствия последействия, ординарности. Параметр потока отказов, характеризующий его интенсивность, является постоянной величиной для любого момента времени в период нормальной эксплуатации при неизменных условиях.

При постоянной величине параметра потока отказов время безотказной работы объекта имеет экспоненциальное распределение.

Вероятность появления n отказов в простейшем потоке на любом заданном интервале времени в период нормальной эксплуатации будет иметь экспоненциальное распределение.

Вероятность безотказной работы объекта на любом заданном интервале времени в период нормальной эксплуатации имеет экспоненциальное распределение:

P(t)=P(T>t)=exp(-t).

Среднее время между отказами (наработка на отказ) в периоде нормальной эксплуатации

T_cp=,

т.е. равно величине, обратной параметру потока отказов.

Экспоненциальное распределение времени восстановления работоспособности объекта является самым распространенным в теории надежности, т.к. на практике поток восстановлений чаще всего является простейшим. Особая роль экспоненциального распределения времени восстановлений определяется его характеристическим свойством: при восстановлении работоспособности объекта распределение оставшегося времени восстановления не зависит от того, сколько времени восстановление уже продолжалось.

Интегральная функция экспоненциального распределения времени восстановления работоспособности имеет вид

F_B(t)=P(T_B<t)=1-exp(-t).

Дифференциальная функция распределения (плотность вероятности):

f_B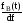(t)== exp(-t).

Интенсивность восстановлений работоспособности постоянна:

(t)==.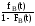

Среднее время восстановления:

T_в.cp.=(-t)dt=,

т.е. восстановление работоспособности обратно пропорционально интенсивности.

Экспоненциальное распределение хорошо описывает случаи, когда основная масса восстановлений выполняется быстро, а задержки в восстановлении наблюдаются редко, т.е. когда число восстановлений уменьшается с увеличением их длительности. Конечно, экспоненциальное распределение времени восстановления работоспособности объектов не является универсальным и единственно возможным.

Пропускная способность системы восстановления работоспособности сравнительно мало зависит от вида распределения, а зависит в основном от его среднего значения. Поэтому в теории надежности чаще всего пользуются экспоненциальным распределением, что позволяет упростить математический аппарат при небольшой погрешности.