4.3. Борьба с флуктуационными, сосредоточенными и импульсными помехами.

4.3.1 Флуктуационные помехи

Борьба с флуктуационными помехами (шумами) является од­ной из центральных задач обеспечения помехоустойчивости систем радиосвязи. Флуктуационные помехи всегда присутствуют в канале радиосвязи и их невозможно полностью подавить из-за их физической природы. Выбросы флуктуационной помехи могут иметь значительную величину и ее порой трудно отличать от сиг­нала, даже в его отсутствие. С другой стороны, интерференция сигнала и помехи может привести к тому, что суммарное колебание окажется ниже порога регистрации и сигнал не будет зафик­сирован.

Для борьбы с флуктуационными помехами может использоваться любой из методов, рассмотренных в главе 4.2. Однако ниже остановимся главным образом на тех методах борьбы с флуктуационными помехами, которые позволяют увеличить среднюю мощность сигнала, поскольку качество связи определяется отношением средней мощности сигнала к мощности шума в полосе пропускания приемника.

Известно, что при передаче непрерывных сигналов средняя мощность передатчика оказывается значительно ниже максималь­ной. Самым очевидным способом повышения средней мощности сигнала в этом случае является сокращение динамического диапазона сигнала. Этого можно достичь путем преобразования не­прерывных сигналов в цифровые, а применительно к речевым сигналам, еще и клипированием или компандированием сигнала (см. главу 3.1.2).

В реальных средствах радиосвязи наиболее распространенным методом борьбы с флуктуационными помехами является фильтрация сигналов. Ниже остановимся на отыскании оптимальных условий фильтрации дискретных и непрерывных сигналов.

При фильтрации дискретных сигналов u_c1(t) и u_c2(t), которые могут представлять двоичный сигнал, условие оптимального приема при действии флуктуационных помех будет определяться неравенством [2]:

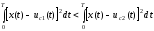. (4.6)

В (4.6) сигнал x(t) на входе приемника представляет собой сумму переданного сигнала u_c(t) и помехи u_n(t) на конечном интервале 0 < t < Т.

Оптимальным приемником можно считать такой приемник, ко­торый воспроизводит переданный сигнал u_c(t) с наименьшим среднеквадратическим отклонением от принятого сигнала x(t).

В.А. Котельников предложил оценивать качество работы приёмника на основе минимума полной вероятности ошибки (см. главу 2 формулу (2.17)). Приёмник, работающий на этом принципе был назван идеальным приёмником, а сам критерий, положенный в основу оценки качества его работы, критерием идеального наблюдателя. На практике наибольшее распространение получили критерий идеального наблюдателя и критерий Неймана-Пирсона, в соответствии с которым приёмник минимизирует вероятность пропуска цели Р_пц при заданном значении вероятности ложной тревоги Р_лт. В дальнейшем будем придерживаться определения оптимальности приёмника в смысле Котельникова и определим структуру такого оптимального приёмника.

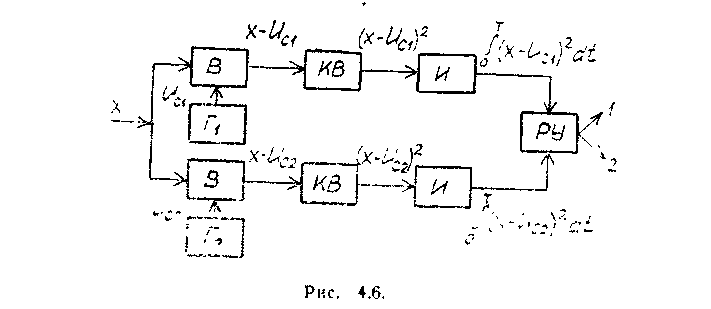
Одной из схем, реализующей условие (4.6), может быть схема приемника, приведенная на рис. 4.6. Такой приемник был пред­ложен В. Л. Котельниковым

В этом приемнике генераторы опорных сигналов Г₁ и Г₂ фор­мируют соответственно передаваемые сигналы u_c1, и u_c2.С вы­читающих устройств В сигналы вида х — и_с1, и х — и_сг поступа­ют на квадратирующие устройства KB и преобразуются к виду (х – и_с1)² и (х — u_c2)². Затем эти сигналы интегрируются на интервале Т и после интеграторов II колебания и 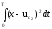подаются на решающее устройство РУ, представляющее собой схему сравнения и выбора.

Выражение (4.6) можно преобразовать к эквивалентному не­равенству, если выполнить операцию возведения в квадрат подын­тегральных выражений

, (4.7)

где 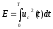— энергия сигнала.

Условие (4.7) можно реализовать с помощью схемы так на­зываемого оптимального порогового приемника (рис. 4.7).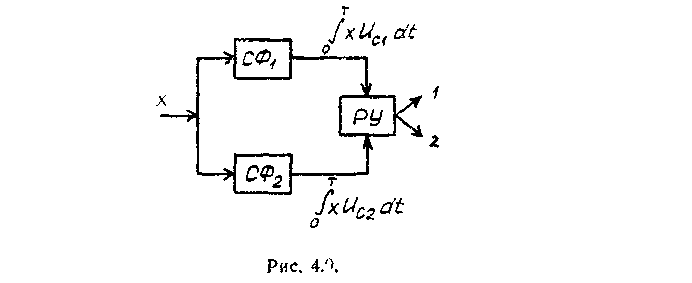

Принимаемое колебание и разностный сигнал перемножаются (П), после чего результат 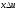интегриру­ется (И) и сравнивается с постоянным порогом, равным 0,5 (E₂-E₁).

Оптимальный пороговый приемник проще приемника В. А. Котельникова и его целесообразно применять в каналах с ад­дитивными помехами. В каналах же с переменными параметра­ми, где уровень сигнала все время изменяется, необходимо порог автоматически регулировать, что является недостатком.

При равенстве энергий сигналов (Е₂ = Е₁) этот недостаток устраняется, поскольку порог равен нулю и решающее устройст­во РУ выдает только лишь знак сигнала.

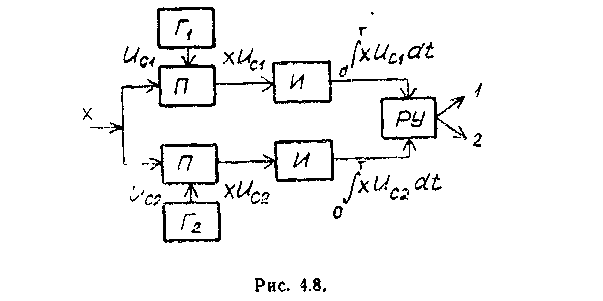
Следует заметить, что в случае E₂=E₁ в приемнике В. А. Котельникова отпадает необходимость в операции квадратирования и он преобразуется в корреляционный когерентный приемник (рис. 4.8), реализующий следующий алгоритм работы:

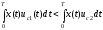. (4.8)

Условие (4.8) можно также реализовать с помощью опти­мального приемника на согласованных фильтрах (рис. 4.9).

При отсутствии помех сигнал на выходе каждого согласован­ного фильтра с точностью до постоянного множителя совпадает с автокорреляционной функцией входного сигнала. При наличии помех напряжение на выходе каждого согласованного фильтра будет пропорционально функции взаимной корреляции принятого сигнала x(t) и переданного сигнала u_c(t).

Первый согласованный фильтр СФ1 выполняет операцию , а второй согласованный фильтр СФ2 — операцию , после чего напряжение с выхода каждого фильтра поступает на решающее устройство РУ.

Величина отклика на выходе согласованного фильтра и на выходе коррелятора при когерентном приеме одинакова и рав­на [3, 5].

. (4.9)

Из (4.9) следует, что отношение сигнал/шум на выходе опти­мального приемника не зависит от формы входного сигнала и ее можно выбирать из условия обеспечения наиболее эффективной борьбы с другими видами помех.

По существу, согласованный фильтр эквивалентен коррелято­ру. Однако реализовать согласованный фильтр, особенно для ШПС, труднее, чем коррелятор.

На практике при приеме дискретных сигналов широко исполь­зуется квазиоптимальная фильтрация, когда в приемнике приме­няются фильтры, согласованные с сигналом лишь по полосе. В случае приема узкополосных дискретных сигналов длительностью Т_с в зависимости от формы сигнала необходимо правильно выбирать амплитудно-частотную характеристику фильтра. Это имеет важное значение для получения максимального отношения сигнал/шум на его выходе. Сказанное иллюстрируется таблицей 4.1, в которой для различных по форме сигналов и АЧХ фильт­ров приведены максимальные нормированные значения отноше­ния сигнал/шум 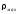на выходе согласованных по полосе фильт­ров.

Таблица 4.1

Вид огибающей сигнала	ЛЧХ фильтра
Прямоугольная Прямоугольная Гауссова Гауссова	Прямоугольная Гауссова Прямоугольная Гауссова	1,37 0.72 0.72 0,63	0,91 0,94 0.94 1,0

В таблице 4.1 = — отношение сигнал/шум на выходе фильтра, согласованного на полосе с сигна­лом, а h²₀ отношение сигнал/шум на выходе согласованного фильтра. Оптимальная полоса фильтра находится из соотношения

.

Из таблицы 4.1 видно, что при равенстве центральных час­тот сигнала и фильтра отношение сигнал/шум на входе решаю­щей схемы при квазиоптимальной фильтрации по сравнению с оп­тимальной фильтрацией снижается незначительно. В то же время реализовать фильтр, согласованный с сигналом по полосе, зна­чительно проще, чем согласованный фильтр. Этим, в частности, можно объяснить широкое применение в средствах радиосвязи фильтров, согласованных с сигналом только по полосе.

Рассмотрим некоторые особенности оптимального приема не­прерывных сигналов при действии флуктуационных помех.

В главе 4.2 уже отмечалось, что оптимальная линейная фильтрация непрерывных сигналов базируется на теории Колмо­горова-Винера, которая верна лишь для стационарных случайных процессов. Однако реальные непрерывные сигналы (телефонные,телеметрические, телевизионные и др.) не всегда являются ста­ционарными, что не позволяет решить задачу построения опти­мальных линейных фильтров на базе теории линейной фильтра­ции. В связи с этим на практике находят применение другие способы построения оптимальных приемников непрерывных сиг­налов.

Если бы передаваемый непрерывный сигнал был полностью известным, подобно тому, как это имеет место при передаче дис­кретных сигналов, то схемы оптимальных приемников для не­прерывных сигналов не отличались бы от рассмотренных выше схем оптимальных приемников. Однако при передаче непрерывных сигналов получатель информации находится в более тяжелых ус­ловиях, поскольку он располагает лишь некоторой информацией о сигнале. Ему могут быть известны рабочая частота, вид моду­ляции, ширина спектра сигнала и т. п. Остальную же информа­цию он должен получить путем анализа принятого сигнала за не­который предшествующий промежуток времени Т.

Анализ принятого колебания x(t) должен способствовать вос­произведению переданного сигнала u_c(t) с минимальным среднеквадратическим отклонением.

Оптимальный приемник путем анализа принятого сигнала x(t) вычисляет плотность распределения вероятностей для всех возможных реализаций передаваемых сигналов. Решение задачи сводится к тому, чтобы вычислить функцию плотности распреде­ления вероятностей .принятого сигнала x(t) за промежуток Т и выдать на выходе приемника ту реализацию передаваемого сиг­нала, для которой эта функция максимальна.

Нахождение плотности распределения вероятностей основано на вычислении взаимной корреляции между принятым колебанием x(t) и переданным ожидаемым сигналом u_c(t). Плотность рас­пределения вероятностей можно представить функцией [2]

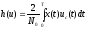, (4.10)

где N₀ — постоянная спектральная плотность шума.

Так как сигнал u_c(t) неизвестен, то вместо сигнала следу­ет брать некоторое его оценочное значение v(t), которое в резуль­тате анализа колебания x(t) полагается близким к переданному сигналу. Поэтому приемник определяет не функцию h(u), а не­которую оценочную эквивалентную ей функцию h(v).

Поясним это положение. Если бы сигнал был полностью из­вестен, как это имело место при приеме дискретных сообщений, то с помощью коррелятора или оптимального фильтра была бы найдена именно функция h(u). При передаче же непрерывных со­общений сигнал известен не полностью. Могут быть известны, как уже отмечалось, только некоторые его параметры, такие, как ра­бочая частота, вид модуляции, ширина спектра и некоторые другие. Сам же передаваемый сигнал неизвестен. При этом сиг­нал меняется непрерывно со временем и может принять любую форму. Наблюдая за принятым колебанием x(t) за предшеству­ющий промежуток Т, приемник должен произвести оценку этого сигнала и вычислить оценочную функцию

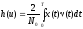, (4.11)

где v(t) — оценочное значение передаваемого сигнала на выхо­де приемника.

Для нахождения h(v) можно воспользоваться либо схемой следящего коррелятора (рис. 4.10), либо схемой, содержащей следящий фильтр, т. е. фильтр с переменными параметрами (рис. 4.11). Обе схемы имеют информационный канал, на выходе кото­рого формируется оценочное значение v(t) передаваемого сигна­ла u_с (t), а также канал обратной связи.

В схеме следящего коррелятора (рис. 4.10) обратный канал, содержащий управляющий элемент УЭ и генератор Г, служит для формирования опорного сигнала, подаваемого на перемножитель П, на вход которого поступает колебание x(t). Управляющий элемент служит для изменения модулируемого параметра рабо­чей частоты, формируемой генератором Г, в соответствии с ве­личиной v(t). Фильтр нижних частот ФНЧ используется в качест­ве интегратора на интервале наблюдения 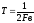(F_в — верхняя частота в спектре передаваемого сигнала).

В схеме со следящим фильтром (рис. 4.11) посредством об­ратного канала, содержащего УЭ, изменяются параметры фильт­ра СФ в соответствии со значением v(t). Поскольку величина v(t) непрерывно меняется, то и параметры фильтра также непре­рывно изменяются, подстраиваясь под ожидаемый сигнал u_с(t).

Следящие оптимальные приемники являются нелинейными устройствами, поэтому теорию оптимального приема непрерывных сигналов следует рассматривать как теорию оптимальной нели­нейной фильтрации.

Следует отметить, что при действии в канале связи как ад­дитивной, так и мультипликативной помехи приемники, приве­денные на рис. 4.10 и 4.11, должны быть дополнены системами автоматической регулировки усиления и фазовой автоподстройкой частоты, а при изменяющейся величине N₀ — устройством изме­рения и выравнивания помех.

Таким образом, при оптимальном приеме сигналов, передава­емых по каналам с переменными параметрами и непостоянным уровнем помех, в приемнике должно автоматически осуществ­ляться непрерывное слежение за формой сигнала и характером помехи, а это значит, что оптимальный приемник должен быть адаптивным.