5.2. Основное уравнение аналитической динамики

Движение материальных систем с идеальными связями подчиняется следующему основополагающему правилу: сумма элементарных работ всех действующих на систему активных сил, включая силы инерции, на возможных перемещениях равна нулю:

где – элементарная работа силы инерции i-й точки ; – масса точки; – вектор ускорения.

Существенно, что выполнение этого общего уравнения аналитической динамики необходимо и достаточно для полного описания движения системы.

Напомним, что момент сил инерции тела, вращающегося вокруг неподвижной оси, М^(J) = I, где I – момент инерции относительно оси;  – угловое ускорение; знаки минус и плюс соответствуют ускоренному и замедленному вращению.

Пример 5.2. Два тела, связанные невесомой нерастяжимой нитью, движутся вдоль абсолютно гладких наклонной и горизонтальной плоскостей. Нить переброшена через неподвижный блок с известными радиусом r и моментом инерции I (рис.5.10). Определить ускорение и натяжение нити T в сечении ab.

Решение. Вследствие нерастяжимости нити модуль ускорения тел w одинаков. Угловое ускорение блока  = /r. Аналогично возможный поворот блока , где s – перемещение системы; Р₁ – вес первого тела, . Поэтому основное уравнение динамики имеет вид

.

Сократим это уравнение на s, решим его относительно w:

.

Натяжение нити в сечении ab

.

Задача 5.9. Три груза массы соединены нерастяжимой нитью, переброшенной через неподвижный блок (рис.5.11). Первый груз движется по вертикали, а два других – по горизонтальной гладкой поверхности. Определить ускорение системы и силу натяжения в сечении ab. Массами нити и блока пренебречь.

Ответ: .

Задача 5.10. Два груза с массами и подвешены на невесомых нерастяжимых нитях, которые навернуты на внутренний и внешний радиусы бицилиндра, вращающегося вокруг неподвижной оси (рис.5.12). Определить угловое ускорение бицилиндра.

Ответ: .

Задача 5.11. К системе блоков (рис.5.13) подвешены два груза (= 10 кг, = 8 кг). Пренебрегая массами блоков, определить ускорение второго груза и натяжение нити.

Ответ: w₂ = 2,8 м/с²; Т = 56,1 Н.

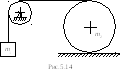
Задача 5.12. Груз массой приводит в движение каток массы при помощи невесомой нерастяжимой нити (рис.5.14). Пренебрегая массой блока, определить ускорение груза. Каток катится без проскальзывания и представляет собой однородный диск.

Ответ:

5.3. Уравнения Лагранжа 2-го рода

Для составления уравнений Лагранжа необходимо следующее:

1) правильно выбрать обобщенные координаты q₁, q₂, …, q_n, которые должны быть взаимно независимы и полностью определять положение системы в пространстве;

2) определить обобщенные силы Q₁, Q₂, …, Q_n, по всем обобщенным координатам. Если действующие активные силы носят потенциальный характер, то , где – потенциальная энергия системы;

3) представить кинетическую энергию системы как функцию обобщенных координат и скоростей ;

4) осуществить операции частного и полного дифференцирования в соответствии с видом уравнений Лагранжа

n ().

Таким образом, движение системы с n обобщенными координатами полностью описывается n уравнениями Лагранжа. Они образуют систему n дифференциальных уравнений второго порядка с n неизвестными.

Пример 5.3. В эпициклическом механизме бегающая шестеренка радиусом насажена на кривошип, который вращается вокруг оси неподвижной шестеренки под действием движущего момента (рис.5.15). Кривошип – однородный стержень длиной и массой Бегающая шестеренка – однородный диск массой , который перекатывается по неподвижной шестеренке без проскальзывания. Следует учесть момент сопротивления ее перекатыванию. Составить уравнения Лагранжа.

Решение. Система имеет одну степень свободы и одну обобщенную координату  – угловое отклонение кривошипа от горизонтали. Момент инерции кривошипа относительно оси его вращения , а центральный момент инерции . Кинетическая энергия кривошипа .

Бегающая шестеренка находится в режиме чистого качения, причем мгновенный центр скоростей расположен в точке касания Р. Поэтому ее угловая скорость где – скорость точки , по модулю Следовательно, кинетическая энергия этой шестеренки , причем, согласно теореме Штейнера, момент инерции относительно мгновенной оси вращения

.

После подстановки получим

.

Общая кинетическая энергия

Сообщим кривошипу возможный поворот . Возможные повороты связаны между собой точно так же, как соответствующие угловые скорости. Поэтому возможный поворот бегающей шестеренки . Элементарная работа активных сил

.

Таким образом, обобщенная сила

.

Единственное уравнение Лагранжа имеет вид

.

Учтем, что

; ; ,

поэтому окончательно получим

.

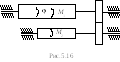
Задача 5.13. Передача вращения между двумя валами осуществляется двумя зубчатыми колесами, имеющими соответственно z₁ и z₂ зубцов (рис.5.16). Моменты инерции валов вместе с колесами и . На ведущий вал действует вращающий момент а на ведомый – момент сопротивления . Составить уравнение вращения ведущего вала.

Ответ: , где i = z₁ / z₂.

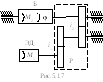
Задача 5.14. Барабан Б центрифуги приводится во вращение электродвигателем ЭД через двухступенчатый редуктор Р (рис.5.17). Заданы моменты инерции электродвигателя (), барабана () и промежуточного вала редуктора (), а также передаточные числа ступеней редуктора ( и ). К электродвигателю приложен вращающий момент а к барабану – момент сопротивления Составить уравнение вращения барабана.

Ответ:

Задача 5.15. Составить уравнение движения маятника, который состоит из материальной точки М массой m, подвешенной на невесомой нити, навернутой на неподвижный цилиндр радиусом а (рис.5.18). В положении равновесия длина свисающей части нити l.

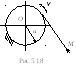
Ответ:

Задача 5.16. Составить уравнение движения математического маятника массы , длина которого меняется по заданному закону .

Ответ: , где  – угол отклонения нити от вертикали.

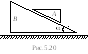
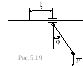З адача 5.17. Точка подвеса маятника движется по горизонтальной прямой по заданному закону (рис.5.19). Составить уравнение движения маятника.

Ответ: .

Задача 5.18. Призма массой скользит по гладкой боковой грани призмы массой , образующей угол с горизонтом (рис.5.20). Определить ускорение призмы B. Силами трения пренебречь.

Ответ: .

Задача 5.19. Составить уравнение движения однородного прямолинейного стержня длиной который своим левым концом опирается о гладкую вертикальную стену, а в промежуточной точке на неподвижный гвоздь О, отстоящий от стенки на расстояние а (рис.5.21). Угол  задан.

Ответ: .

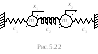
Задача 5.20. Составить уравнения движения двухмассовой упругой системы (рис.5.22). В качестве обобщенных координат принять текущие смещения тел и от их равновесных положений.

Ответ: ; , где с₁, с₂ и с₃ – жесткость пружин.

Задача 5.21. Тележка массой катится вдоль горизонтальной поверхности (рис.5.23). К корпусу тележки шарнирно присоединен физический маятник. Масса маятника эксцентриситет момент инерции относительно оси вращения Составить уравнение вращения. В качестве обобщенных координат принять абсолютное перемещение корпуса х и угловое отклонение эксцентриситета от вертикали .

Ответ: ;