3.2. Колебательное движение

3.2.1. Свободные колебания материальной точки

Свободные колебания – это колебания, осуществляемые под действием только восстанавливающей силы упругости, т.е. силы, пропорциональной по величине смещению точки из положения равновесия.

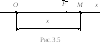
При перемещении точки М вдоль оси Ох сила упругости направлена к положению равновесия О (рис.3.5) и ее проекция , где с – жесткость подвески точки М, Н/м (здесь знак минус показывает, что направлена против смещения х). Дифференциальное уравнение свободных колебаний (без сопротивления) имеет вид

или

.

Его решение в общем виде

где – круговая частота свободных колебаний, с^-1.

Постоянные интегрирования можно определить из начальных условий: при Тогда

(3.1)

Другая форма решения уравнения свободных колебаний имеет вид

где а – амплитуда колебаний;  – начальная фаза,

.

Пример 3.3. Груз массой m = 10 кг на пружине с жесткостью с = 2000 Н/м совершает колебания на плоскости с углом наклона 30 (рис.3.6). В начальном положении пружина была сжата относительно недеформированного состояния на величину м и груз опущен без начальной скорости. Найти закон колебаний, отсчитывая координату х от положения статического равновесия груза. Найти также наибольшее значение силы упругости пружины при колебаниях.

Решение. На рис.3.6 показаны силы, действующие на груз М, а также О – начало отсчета координаты х, А – положение недеформированной пружины, начальное положение груза, причем статическая деформация пружины, начальная деформация. Проекция силы упругости и дифференциальное уравнение движения можно представить в виде

(3.2)

В положении статического равновесия поэтому

м

(здесь принято  м/с²). Теперь уравнение движения принимает классический вид (3.2).

Круговая частота и период колебаний соответственно

с.

Начальная координата груза м. Поскольку по формуле (3.1) находим закон колебаний: м. Амплитуда колебаний м. Максимального значения сила упругости пружины достигает при ее максимальной деформации, когда груз отклонится вниз на величину при этом максимальная деформация и соответственно

 Н.

Задача 3.22. Груз массой 98 г подвешен к недеформированной пружине и отпущен без толчка. Для деформации пружины на 1 см к ней следует приложить силу, равную 0,141 Н. Найти уравнение колебаний, отсчитывая координату х вниз из положения статического равновесия груза.

Ответ: м.

Задача 3.23. Под действием груза, подвешенного к концу вертикальной пружины, она получает статическое удлинение  м. Найти закон колебаний, а также амплитуду и период колебаний, если в начальный момент груз находился в положении равновесия и ему сообщили начальную скорость  м/с, направленную вверх.

Ответ:  м;  м; T = 0,45 с.

Задача 3.24. При равномерном спуске на тросе груза весом P = 20 кН со скоростью 5 м/с вследствие защемления верхнего конца троса в обойме блока произошла его неожиданная задержка. Определить наибольшее натяжение троса при последующих колебаниях груза, если коэффициент жесткости троса с = 4 МН/м. Весом троса пренебречь.

Ответ: Т_max = 0,47 МН.

Задача 3.25. Груз Q падает с высоты h = 1 м без начальной скорости на горизонтальную балку в ее середине и совершает затем безотрывные колебания вместе с балкой, концы которой закреплены. Найти закон колебаний груза, отсчитывая координату x вниз из положения его статического равновесия, если статический прогиб в середине балки при нагрузке Q составляет 0,5 см. Массой балки пренебречь.

Ответ:  м.

Задача 3.26. Тело, прикрепленное к пружине, находится на гладкой плоскости под углом 30 к горизонту. Статическое удлинение пружины Определить закон колебаний груза, если в начальный момент пружину растянули из недеформированного состояния на длину 3f и груз отпустили без толчка.

Ответ: .

Задача 3.27. Тело массой 12 кг совершает на вертикальной пружине гармонические колебания. За 45 с оно совершило 100 полных колебаний, после чего к пружине прикрепили дополнительный груз массой 6 кг. Определить период колебаний системы с обоими грузами.

Ответ: Т = 0,55 с.

Задача 3.28. Найти жесткость с пружины, эквивалентной двойной пружине, состоящей из двух последовательно соединенных пружин с коэффициентами жесткости с₁ и с₂. Определить также период колебаний груза весом Q на такой двойной пружине.

Ответ: ;

Задача 3.29. Груз весом Р = 98 Н находится на горизонтальной гладкой плоскости. Слева и справа он соединен с двумя горизонтальными пружинами жесткостью с₁ = 40 Н/см, с₂ = 50 Н/см. В положении равновесия пружины недеформированы. В начальный момент груз смещен вправо на 4 см из положения равновесия (в сторону оси х) и ему сообщена в ту же сторону начальная скорость v₀ = 90 м/с. Найти уравнение движения и период колебаний груза.

Ответ:  м,  рад.

Задача 3.30. Груз весом Р подвешен к концу В эластичного шнура, верхний конец которого закреплен в точке А. Груз поднимают в точку А и затем отпускают без начальной скорости. Найти наибольшее удлинение шнура, если его естественная длина (без груза) равна , а статическое удлинение при действии силы Р равно

Ответ:

Задача 3.31. Стержень ОА длиной l, весом которого можно пренебречь, закреплен шарнирно в точке О и на конце А имеет груз массой m (рис.3.7). К стержню на расстоянии а от оси шарнира прикреплена пружина жесткостью с. Считая груз точечной массой, определить его собственную частоту колебаний k, если в положении равновесия стержень ОА занимает горизонтальное положение.

Ответ: