2.5. Сложное движение точки

Движение точки по отношению к системе подвижных осей координат x₁, y₁, z₁ (рис.2.20), которые, в свою очередь, движутся относительно условно неподвижной системы координат Оxyz, называется сложным. Движение точки по отношению к системе подвижных осей координат x₁, y₁, z₁ называется относительным движением, а движение тела, с которым связана подвижная система координат О₁x₁y₁z₁, относительно неподвижной системы осей x, y, z называется переносным.

Скорость точки в сложном движении (теорема сложения скоростей)

,

где – скорость точки относительно условно неподвижной системы отсчета Оxyz (абсолютная скорость); – скорость точки относительно подвижной системы отсчета О₁x₁y₁z₁ (относительная скорость); – скорость той точки тела, с которым связана подвижная система координат О₁x₁y₁z₁, через которую в данный момент проходит рассматриваемая точка (переносная скорость).

Для определения относительной скорости точки следует мысленно остановить переносное движение и вычислить относительную скорость по правилам кинематики точки.

Для определения переносной скорости надо мысленно прекратить относительное движение и искать переносную скорость по правилам кинематики точки как скорость той точки тела, с которым связана подвижная система координат и с которой совпадает в данный момент рассматриваемая точка.

Для определения ускорения точки в сложном движении следует рассматривать два случая:

 при поступательном переносном движении

,

где – ускорение точки относительно условно неподвижной системы отсчета Оxyz (абсолютное ускорение); – ускорение той точки тела, с которым связана подвижная система координат О₁x₁y₁z₁, через которую в данный момент проходит рассматриваемая точка (переносное ускорение); – ускорение точки относительно подвижной системы отсчета О₁x₁y₁z₁ (относительное ускорение);

 при вращательном переносном движении

,

где – поворотное ускорение, или ускорение Кориолиса, ; – угловая скорость подвижной системы отсчета (переносного движения).

Пример 2.5. Корабль плывет вдоль меридиана CBN с юга на север (рис.2.21). Его скорость по отношению ко дну равна 36 км/ч. Определить составляющие абсолютной скорости и абсолютного ускорения корабля, учитывая вращение Земли вокруг своей оси. Широта места  = 60, радиус Земли R = 6,410⁶ м.

Решение. Корабль, находящийся в точке В, участвует одновременно в двух движениях:

 переносном – вращении вместе с Землей вокруг оси ON с угловой скоростью с^-1. В переносном движении точка В земной поверхности описывает окружность с центром в точке А и радиусом АВ;

 относительном – корабль описывает дугу CBN окружности радиусом R с центром в точке О.

Абсолютная скорость корабля .

Переносная скорость по модулю

м/с = 232 м/с

и направлена по касательной к 60-й параллели с запада на восток.

Относительная скорость согласно условию v_r = 36 км/ч = = 10 м/с и направлена по касательной к меридиану CBN с юга на север.

Абсолютное ускорение . Так как переносное движение – равномерное вращение вокруг оси, то переносное ускорение является переносным нормальным ускорением:

w_e = _eАВ = _eRcos60 = 0,017 м/с²

с направлением от точки В к точке А.

Относительное движение осуществляется с постоянной по величине скоростью по дуге окружности радиусом R. Следовательно, относительное ускорение будет нормальным относительным ускорением:

м/с²,

направленным от точки В к точке О.

Кориолисово ускорение

w_c = 2_ev_rsin= 7,2710^-5sin60 = 1,2610^-3 м/с².

Кориолисово ускорение направлено по касательной к 60-й параллели северной широты с востока на запад.

Задача 2.24. Вращение диска вокруг своей оси соответствует закону  = 1,5t² рад. Вдоль радиуса диска в направлении от центра к его ободу движется точка М. Определить величину абсолютной скорости этой точки в момент t = 1 с, если ее движение относительно диска задано уравнением s = OM = 0,1(1 + t²) м.

Ответ: м/с.

Задача 2.25. Определить величину абсолютной скорости точки ротора паровой турбины, ось которого горизонтальна и лежит в диаметральной (продольной) плоскости симметрии судна, идущего со скоростью 20,6 м/с. Расстояние данной точки от оси вращения 60 см. Скорость вращения ротора 3000 мин^-1.

Ответ: v = 189 м/с.

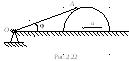
Задача 2.26. Стержень ОА длиной приводится во вращательное движение вокруг неподвижной точки О кулачком, имеющим форму полуокружности радиусом (рис.2.22). Определить угловую скорость стержня в тот момент, когда стержень составляет угол  = 30 с горизонталью, а кулачок движется поступательно со скоростью u.

Ответ: .

З адача 2.27. Крановая тележка А (рис.2.23) движется по стреле крана равноускоренно из состояния покоя и, пройдя расстояние ОА = 2 м, имеет скорость 2 м/с относительно стрелы. Определить для этого момента абсолютное ускорение тележки, если кран вращается равномерно со скоростью n = 30 /  мин^-1.

Ответ: w_a = 4,12 м/с².

Задача 2.28. Башенный кран со стрелой ОС (рис.2.23) вращается равномерно с угловой скоростью  = 2 рад/с. Тележка А имеет в данный момент скорость v₁ = 3 м/с и ускорение w₁ = 4 м/с² по отношению к стреле ОС. Груз В опускается равномерно вертикально вниз. Чему равна величина абсолютного ускорения груза в тот момент, когда расстояние ОА = 3 м?

Ответ: w_a = 14,42 м/с².

Задача 2.29. Плоскость xOy , в которой движется точка согласно уравнениям x = t², y = 4 – t² (x, y – в метрах, t – в секундах), вращается с постоянной угловой скоростью рад/с вокруг оси Oz. Найти абсолютное ускорение точки, когда она находится на кратчайшем расстоянии от оси вращения.

Ответ: при вращении плоскости по движению часовой стрелки w_a = 17,2 м/с²; при вращении в противоположном направлении w_a = 6,325 м/с².

Задача 2.30. Диск вращается в своей плоскости вокруг точки О с некоторой постоянной угловой скоростью, а точка М равномерно движется по окружности диска, обходя его 2 раза за время одного оборота. Зная, что в момент, когда  = 90, абсолютное ускорение точки М  w_a =м/с², определить угловую скорость диска , если его радиус 1 м. Направления движения точки и вращения диска указаны на рис.2.24.

Ответ: 1 рад/с.