
- •Электротехника и электроника
- •1.1 Общие сведения
- •1.2 Резистивные элементы
- •1.3 Индуктивный и емкостный элементы
- •1.4 Источники постоянного напряжения
- •2 Электрические цепи постоянного тока
- •2.1 Общие сведения
- •2.2 Законы Кирхгофа
- •2.2.1 Первый закон Кирхгофа.
- •2.2.2 Второй закон Кирхгофа.
- •2.3 Распределение потенциала вдоль электрической цепи
- •2.4 Последовательное и параллельное соединения резистивных элементов
- •2.4.1 Последовательное соединение.
- •2.4.2 Параллельное соединение
- •2.5 Соединение резисторов треугольником и звездой
- •2.6 Электрическая энергия и мощность
- •2.7 Номинальные величины источников и приемников.
- •3 Линейные однофазные электрические цепи синусоидального тока
- •3.1 Основные величины, характеризующие синусоидальные ток,
- •3.1.1 Мгновенное значение.
- •3.1.2 Действующее и среднее значения синусоидальных токов и напряжений.
- •3.1.3 Изображение синусоидальных токов, напряжений и эдс
- •3.2 Элементы электрических цепей синусоидального тока
- •3.2.1 Резистивный элемент (рэ).
- •3.2.2 Индуктивный элемент.
- •3.2.3 Емкостный элемент.
- •3.3 Расчет неразветвленной электрической цепи синусоидального тока
- •3.4 Мощность в линейных цепях синусоидального тока
- •4 Трехфазные линейные электрические цепи синусоидального тока
- •4.1 Трехфазный источник электрической энергии
- •4.2 Анализ электрических цепей при соединении трехфазного источника и приемника по схеме «звезда» с нулевым проводом
- •4.3 Соединение приемника по схеме «треугольник»
- •4.4 Мощность трехфазной цепи
- •5 Электрические измерения и приборы
- •5.1 Системы электрических измерительных приборов
- •5.2 Основные характеристики электрических измерительных приборов
- •5.2.1 Статическая характеристика.
- •5.2.2 Погрешность.
- •5.2.3 Класс точности.
- •5.2.4 Вариация.
- •5.2.5 Цена деления.
- •5.2.6 Предел измерения.
- •5.2.7 Чувствительность.
- •5.3 Измерение тока, напряжения и мощности
- •5.3.1 Измерение тока.
- •5.3.2 Измерение напряжения.
- •5.3.3 Измерение мощности электрического тока.
- •6 Электрические трансформаторы
- •6.1 Общие сведения
- •6.2 Принцип действия электрического трансформатора
- •6.3 Работа электрического трансформатора в режиме холостого
- •6.4 Опыт короткого замыкания
- •6.5 Мощность потерь в трансформаторе
- •6.6 Автотрансформаторы
- •7 Электрические машины
- •7.1 Общие сведения
- •7.2 Вращающееся магнитное поле
- •7.3 Асинхронные машины
- •7.3.1 Принцип действия асинхронного двигателя (ад).
- •7.3.2 Устройство асинхронного двигателя.
- •7.3.3 Характеристики асинхронного двигателя.
- •7.4 Машины постоянного тока
- •7.4.1 Общие понятия об устройстве машин постоянного тока и принципе их действия
- •7.4.2 Эдс обмотки якоря и электромагнитный момент.
- •7.4.3 Электрические двигатели постоянного тока.
- •7.4.4 Способы регулирования скорости двигателя постоянного
- •7.4.5 Пуск электродвигателей постоянного тока.
- •8 Основы промышленной электроники
- •8.1 Общие сведения
- •8.2 Полупроводниковые диоды
- •8.3 Выпрямители на полупроводниковых диодах
- •8.4 Транзисторы
- •8.4.1 Общие сведения.
- •8.4.2 Усилители на транзисторах.
- •1 U выхn
- •9 Электробезопасность
- •9.1 Общие сведения
- •9.2 Защитное заземление
- •9.3 Зануление
- •9.4 Конструкция заземлителя
- •Список использованных источников
3.1.2 Действующее и среднее значения синусоидальных токов и напряжений.
Согласно закону Джоуля-Ленца тепловая энергия Q, выделяемая в резисторе с сопротивлением R при протекании по нему постоянного тока I0 в течение промежутка времени t равна:
0
Для синусоидального тока формулу (3.7) можно применить лишь для определения тепловой энергии dQ, выделившейся в резисторе с сопротив- лением R за бесконечно малый промежуток времени dt, в течение которого силу тока i можно считать не изменяющейся:
dQ i 2 Rdt , (3.8)
За период времени Т выделившаяся энергия:
103
T
Q ∫ i 2 Rdt , (3.9)
0
Пусть i I m sin t , тогда:
T T I 2
m
tRdt I 2 R sin 2 tdt m RT
2
0 0
m ∫
 I
I
m
I
I
m
2
, называемую действующим значением си-
нусоидального тока, и, подставив ее в последнее выражение, получим:
Q I 2 RT , (3.10)
Сопоставив формулу (3.10), полученную для синусоидального тока, с формулой (3.7), справедливой для постоянного тока, делаем вывод: Дей- ствующее значение синусоидального тока равно такому значению посто- янного тока, который за один период выделяет в том же резисторе та- кое же количество тепла, как и синусоидальный ток.
Аналогично
существуют понятия действующих значений
синусои-
дальных напряжений и ЭДС:
 U
U
m и
U
U
m и
2
 E
Em
. (3.11)
E
Em
. (3.11)
2
Из формул (3.9) и (3.10) получаем:
T
 I
T
∫
i
I
T
∫
i
0
dt . (3.12)
В силу (3.12) действующее значение синусоидального тока часто называют среднеквадратичным или эффективным значениями.
Действующие значения токов и напряжений показывают большинст-
во электроизмерительных приборов (амперметров, вольтметров).
В действующих значениях указываются номинальные токи и напря-
жения в паспортах различных электроприборов и устройств.
 Под
средним
значением
синусоидального
тока
понимают
его
среднее
значение
за
полпериода:
Под
средним
значением
синусоидального
тока
понимают
его
среднее
значение
за
полпериода:
 T
T
1 2 2
 I
ср
T
I
ср
T
2
∫ I m sintdt
I m , (3.13)
104
 т.е. среднее значение синусоидального тока составляет
т.е. среднее значение синусоидального тока составляет
2 =0,638 от
амплитудного значения. Аналогично,
Eср
2Еm /
, U ср 2U m / .
3.1.3 Изображение синусоидальных токов, напряжений и эдс
комплексными числами и векторами.
Синусоидально изменяющийся ток i
числом:
изображается комплексным
i I m sint i
⇔ I m e
j t i
. (3.14)
 Принято
изображение
тока
находить
для момента
времени t=0:
Принято
изображение
тока
находить
для момента
времени t=0:
j i
i I m sin i I&m ⇔ I m e
. (3.15)
Величину
I&m
называют комплексной амплитудой тока или ком-
плексом амплитуды тока.
Под комплексом действующего значения тока или под комплексом тока I& понимают частное от деления комплексной амплитуды тока на
 2
:
2
:
I&
I&m
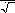 2
2
 I
m
⋅
e
j
i
I
m
⋅
e
j
i
2
I ⋅ e j i , (3.16)
ния
 Под
комплексами
напряжения
и
ЭДС
понимают
подобные
выраже-
Под
комплексами
напряжения
и
ЭДС
понимают
подобные
выраже-
 U&
U&
m
U&
U&
m
2
U ⋅ e j u ,
E& E& m
 2
2
E ⋅ e j e .
+j




 I
=
I
I
=
I
 e
j
i
e
j
i


 Jm
I
=
I
sin
i
Jm
I
=
I
sin
i
 i
i

 Re
I
=
I
Re
I
=
I
+1
 cos
i
cos
i
Рисунок 3.3 – Изображение синусоидального тока на комплексной плоскости вектором I&
Комплексы тока, напряжения и ЭДС изображаются также на ком-
плексной плоскости векторами. Например, на рисунке 3.3 изображен век-
тор
I& . При этом угол i
отсчитывается от оси +1 против часовой стрелки,
105
если i >0. Из рисунка 3.3 следует, что комплекс тока I& (так же, как ком-
плекс напряжения и ЭДС) можно представить а) вектором I& ;
б) комплексным числом в показательной, алгебраической и тригоно-
метрической формах:
I& I ⋅ e j i
Re I&
jJmI& I cos
jI sin , (3.17)
Пример 3.1 Ток
i 2 sint 300
А. Записать выражение для
комплексной амплитуды этого тока.
0
Решение. В данном случае
I m =2 А, =30 . Следовательно,
I&m
0
2 cos 300
j ⋅ 2 sin 300
 3
j
⋅1
А.
3
j
⋅1
А.
Пример 3.2 Комплексная амплитуда тока
I&m
25 ⋅ e
− j 300
А. Записать
выражение для мгновенного значения этого тока.
Решение. Для перехода от комплексной амплитуды к мгновенному
значению надо умножить
I&m
на e jt
и взять коэффициент при мнимой
части от полученного произведения:
i Jm
0
Jm
25 ⋅ e j t −300
25 sint − 300 .
Пример 3.3 Записать выражение комплекса действующего значения тока для примера 3.1.
Решение:
I&
I&m
 2
2

2
⋅
e
2
⋅
e
j 300
2
0
