978-966-10-2413-6_Matematuka 11_rus

мает лишь в одной точке (рис. 7). Поэтому при b > 0 уравнение

ax = b имеет единственный корень. Эти рассуждения приводят к определению логарифма.

Логарифмом числа b > 0 по основанию а, где а > 0, а ≠ 1, называется такое число с, что ас = b.

Другими словами, логарифм числа b с основанием а — это по- казатель степени с, в которую нужно возвести а, чтобы получить b . Символично это записывают так: c = loga b (читается: лога-

рифм числа b по основанию а).

Так как логарифм числа b по основанию а — решение уравне- ния ax = b , то имеем равенство

aloga b = b.

Его еще называют основным логарифмическим тожде-

ством.

Отметим, что логарифмы отрицательных чисел не существуют,

так как при отрицательных значениях b уравнение ax = b кор- ней не имеет.

Логарифм — от греческих λογος (logos) — слово, уче- ние, ум, отношение и αριθµος (arithmos) — число, счет, номер.

Пример 1. Найти: 1) log2 32; 2) log3 19 ; 3) log4 2; 4) log10 1 ;

5) 5log5 23 .

 1) По определению логарифма, log2 32 – это такое число х,

что 2x = 32 . Уравнение2x = 32 имеет единственное решение х = 5, которое легко найти путем подбора (25 = 32). То есть log232 = 5.

2) Аналогично, log3 19 = −2, так как 3−2 = 19 .

4)log10 1 = 0, так как 100 =1.

5)На основании основного логарифмического тождества име-

ем: 5log5 23 = 23. g

Ответ. 1) 5; 2) – 2; 3) 0,5; 4) 0; 5) 23.

 По определению логарифма, данное уравнение приводится

к виду: 5x −1 = 32 , или 5x =10. Отсюда х = 2. g

Ответ. 2.

Многочисленные применения логарифмов базируются на их свойствах, вытекающих из определения логарифма и свойств сте- пеней с действительными показателями.

Свойство 1. Логарифм числа 1 по основанию а, где a > 0 , a ¹1, равен 0:

loga1 = 0.

Свойство 2. Логарифм произведения положительных чисел равен сумме логарифмов сомножителей:

если b > 0, c > 0, то loga(bc)= logab + logac.

Свойство 3. Логарифм частного от деления положительных чисел равен разности логарифмов делимого и делителя:

если b > 0, c > 0, то loga bc = logab – logac.

Свойство 4. Логарифм степени положительного числа равен произведению показателя степени на логарифм основания:

если b > 0, то logabр = p logab.

1) По свойству логарифма произведения положительных чисел

Так как показательная функция монотонна, то из равенства степеней числа а следует равенство показателей. Таким образом, свойство доказано. g

Большинство калькуляторов позволяют находить значения де- сятичных и натуральных логарифмов. Если же нужно вычислить логарифм по другому основанию, то следует воспользоваться так называемой формулой перехода к новому основанию.

Свойство 5 ( формула перехода к другому основанию).

Для произвольных положительных а, b, с, а ≠ 1, с ≠ 1,

справедливо равенство:

loga b = logc b . logc a

 Доказательство представим в виде цепочки равенств:

Ответ. 45 .

Иногда приходится восстанавливать число или выражение по его логарифму. Такую операцию называют потенцированием, и она базируется на таком очевидном утверждении: если loga x = loga y ,

то х = у (эквивалентно тому, что из k = l вытекает ak = al ).

Потенцирование — от немецкого potenzieren — воз -

водить в степень; в его основе лежит латинское potentia — способность, сила.

!Использовать свойства 1–5 во время преобразования выражений с логарифмами следует очень осторожно, обязательно проверяя выполнение условий, при кото-

рых они справедливы. В противном случае можно по-

лучить неправильный результат. Например, lg a2 = 2 lg a

лишь при а > 0.

Пример 5. Решить приближенно уравнение (0,9)х = 0,5.

 Согласно определению логарифма, x = log0,9 0,5 . Перейдем к десятичным логарифмам, применив свойство 5:

x = log0,9 0,5 = lglg 0,90,5 .

Воспользовавшись калькулятором, получим х ≈ 6,6. g

Ответ. ≈ 6,6.

Приведенное в примере 5 уравнение возникло при решении задачи о вытекании воды (§ 1, пример 3). Теперь мы можем дать ответ на поставленный там вопрос: нужно около 6,6 единиц вре- мени для того, чтобы количество воды в резервуаре уменьшилось вдвое.

99 Контрольные вопросы

1°. Имеет ли решения уравнение:

2.Как записать с помощью степени с основанием 10 число:

а°) 10 000; б°) 0,0001; в) 3; г) 0,3?

Чему равняется:

ж) loga 1a , a > 0, a ≠ 1; з) log1 a, a > 0, a ≠ 1?

4.Какой знак имеет число: аa) log5 2 ; б) ln 5; в) ln 0,1; г)log0,1 2 ?

5.Чему равно значение выражения: а) 10lg 2+1 ; б)100−3 lg 2 ; в)e2 ln e ?

6.Как представить число 5 в виде степени 10; е; 2?

7.Всегда ли верно равенство:

8.Какое из чисел больше:

2. Свойства и график логарифмической функции

Определив понятие логарифма числа по основанию а, мы научились каждому положительному числу х ставить в соответствие его логарифм loga x . Други-

ми словами, ми ввели функцию

y = loga x, a > 0, a ≠ 1,

которую называют логарифмической.

Областью определения логарифмической функции является множество положительных чисел.

График логарифмической функции y = loga x проходит через точку с координатами (1; 0), ибо loga 1 = 0 . Эта точка симметрична

точке с координатами (0; 1), через которую проходит график про- извольной показательной функции у = ax. Указанные точки сим- метричны относительно прямой у = х. Оказывается, что графики функций у = ax и y = loga x симметричны друг другу относительно

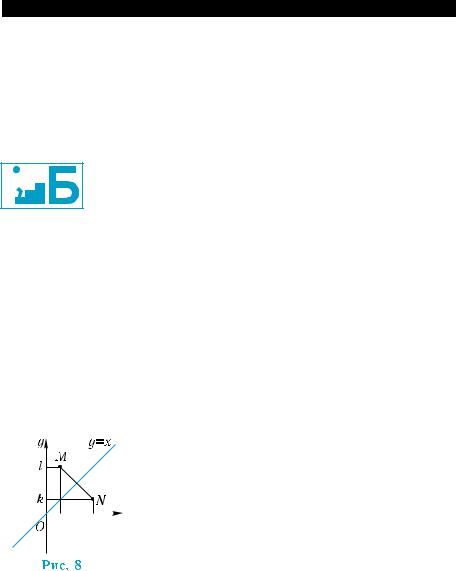
Действительно, если точка М(k; l) принад­ ­ лежит­ графику функции у = ax, то l = ak. Но тогда k = logal и точка N(l; k) принадлежит гра- фику функции y = loga x . Так как точки М(k; l)

и N(l; k) симметричны относительно прямой

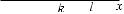у = х (рис. 8), то симметричны относительно этой прямой и графики показательной фун- кции у = ах и логарифмической функции

у = logaх.

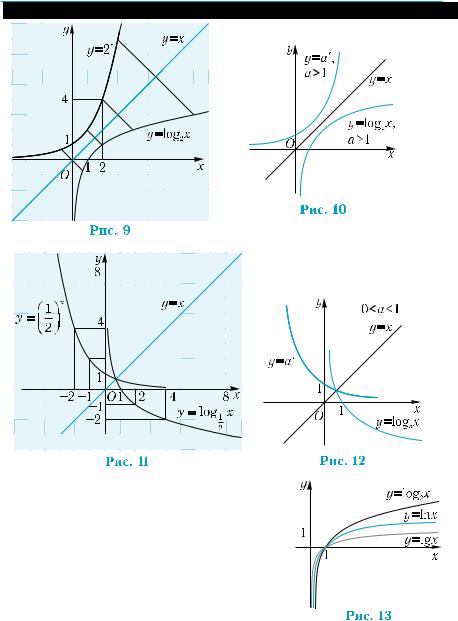
Основываясь на приведенных рассуждениях, можно построить график логарифмической функции. Например, чтобы построить график функции y = log2 x , построим сначала график функции

у = 2x, а затем отобразим его симметрично относительно прямой у = х (рис. 9). Подобные графики имеют логарифмические фун- кции с основанием, большим 1 (рис. 10).

Аналогично строится график функции y = log1 x (рис. 11). Подобные графики

имеют 2логарифмические функции с осно-

ванием 0 < a < 1 (рис. 12).

Анализируя графики логарифмиче- 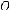ских функций, можно прийти к выводу, что множеством их значений является множество всех действительных чисел, что

при a >1 функции возрастающие, а при

0 < a <1 — убывающие. На рис. 13 изображены графики лога- рифмических функций с различными основаниями, большими 1.

Пример 6. Дана функция y = log3(x + 3). 1) Найти ее область определения.

2) Найти точки пересечения графика этой функции с осями коор- динат.

3) Построить ее график.

2) Чтобы найти точку пересечения графика данной функции с осью у, най- дем значение функции при х = 0: y(0) = log3 (0 + 3) = 1. Итак, график фун-

кции пересекает ось у в точке с коорди- натами (0; 1).Чтобы найти точку пересечения графика с осью х, найдем, при каких значениях х функция обращается в 0:

log3 (x + 3) = 0; x + 3 = 30 ; x + 3 = 1; x = −2 . Итак, график функции пе- ресекает ось х в точке с координатами (−2;0).

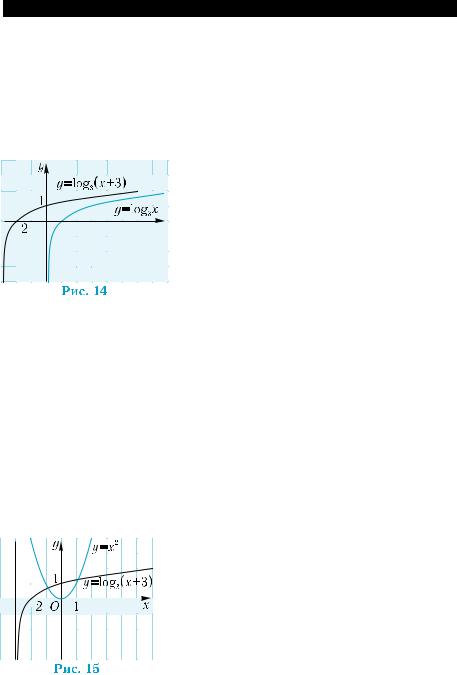
3) График функции можно построить из графика функции

y = log3 x параллельным переносом последнего на 3 единицы в

отрицательном направлении оси абсцисс (рис. 14).

4) Чтобы проверить, проходит ли график функции через точку

и у = x2 . Они пересекаются в двух точках

(рис. 15). Поэтому уравнение имеет два

корня. g

Ответ. 1) (–3; +∞); 2) (0; 1), (–2; 0); 4) через точку А не проходит,

через точку В проходит; 5) два корня.

Обоснуем свойства логарифмической функции, приведенные выше.

Свойство 1.Если a > 1, то функция y = loga x

принимает положительные значения при х > 1 и отрицательные при 0 < x < 1.

Если 0 < a < 1, то функция y = loga x принимает положи-

тельные значения при 0 <x < 1 и отрицательные прих > 1.

 Действительно, пусть a >1 , х > 1. Равенство y = loga x мож-

но записать в виде: х = ау. Из свойств показательной функции (см. §1) следует, что у > 0, то есть loga x > 0 . Аналогично доказыва-

ются остальные сформулированные утверждения. g

Свойство 2. Логарифмическая функция y = loga x яв-

ляется возрастающей, если a > 1, и убывающей, если

0 < a < 1.

тривается аналогично. Советуем это сделать самостоятельно.g

Свойство 3. Множество значений функции y = loga x

совпадает со множеством всех действительных чисел.

 Нужно доказать, что любое действительное число у может быть логарифмом некоторого числа х. Поскольку степень ay опре- делена при любом у, то, положив х =ay , получим:loga ay = y , что и требовалось доказать. g

Говоряоприменениилогарифмическихфункций,нужноиметь в виду то, что потребность в них возникает чаще всего там, где используются показательные функции. Например, пусть зависи- мость атмосферного давления от высоты местности над уровнем моря описана с помощью показательной функции, как в приме-

40 Раздел 1. Показательная и логарифмическая функции

ре 5 §1, тогда высота над уровнем моря определяется через атмос-

ферное давление с помощью логарифмической функции.

С помощью логарифмических функций моделируются некоторые реальные процессы и явления: зависимость скорости ракетыv от ее

массы m задается формулой v = vг ln mm0 , где vг — скорость вылетаю-

щих газов, m0 – стартовая масса ракеты; зависимость коэффициента Dзвукоизоляции стен от давлениярзвука, прошедшего через стену,

задается формулой D = A lg pp0 , где р0 — давление звука до погло-

щения, А — некоторая постоянная.

Логарифмическая функция применяется в сейсмологии. На- пример, магнитуда объемных волн mb (показатель землетрясе-

ния) вычисляется по формуле mb = lgTA + Q(D, h), где A — ампли-

туда колебаний земли (в микрометрах), T — период волны (в секундах) и Q — поправка, зависящая от расстояния D до эпи- центра и глубины h очага землетрясения.

99 Контрольные вопросы

1°. Пересекает ли график функции y = loga x : а) ось х; б) ось у? 2°. Проходит ли график функции y = log0,2 x через точку с коор-

динатами (5; 1)?

3°. При каких значениях х график функции y = log0,5 x располо- жен выше оси абсцисс?

4°. Какой знак имеет число: а) log0,53; б)log0,5

5°. Что больше: 1 или log0,5 0,7 ?

6°. Какова область определения функции: а)у= lg(x– 1); б)у= lg(–х)?

7.Как расположены друг относительно друга графики функций: