
978-966-10-2413-6_Matematuka 11_rus
.pdf
Призмы и цилиндры |
291 |
5°. Является ли призма правильной, если: а) равны все ее боко- вые ребра; б) все ее боковые грани — прямоугольники?
6°. Какую форму может иметь сечение правильной четырех угольной призмы плоскостью, параллельной основанию?
7°. Является ли правильная четырехугольная призма прямо угольным параллелепипедом?
8°. Может ли быть прямоугольник основанием наклонного па- раллелепипеда?
9. Существует ли наклонный параллелепипед, у которого четы- ре грани являются прямоугольниками?
10. Можно ли определить расстояние между противоположными верхним и нижним углами комнаты, пользуясь обычной ли- нейкой?
11. Можно ли пространство «замостить» равными между собой параллелепипедами?
12. Куб с окрашенными гранями и ребром 6 см разрезали на ку- бики с ребром 1 см. Верно ли, что кубиков с неокрашенными гранями будет 27?
13. По стенкам кубического помещения из нижнего угла в про- тивоположный верхний угол необходимо провести электриче- ский провод. Каким должен быть маршрут, чтобы длина про- вода была наименьшей? Сколько таких маршрутов?
14*.Имеется лист бумаги, градуированная линейка и спичечный коробок. Найдите, ничего не вычисляя, длину диагонали, со- единяющей противоположные вершины коробка.
2. Цилиндры
 Цилиндрическая форма предметов, конструкций, зданий встречается на каждом шагу (рис. 228, а–в).
Цилиндрическая форма предметов, конструкций, зданий встречается на каждом шагу (рис. 228, а–в).
Обычный круговой цилиндр (рис. 229) можно представить как фигуру, образованную параллельными и равны- ми между собой отрезками, проведенными из всех точек круга и

292 |
Раздел 5. Геометрические тела и поверхности |
расположенных по одну сторону от его плоскости. Если же соответствующие отрезки откладывать не от точек круга, а от точек произвольной пло- ской фигуры (основания), то мы получим широ-
кий класс пространственных фигур, которые так- же естественно назвать цилиндрами.
Цилиндр — от греческого χυλινδρου
(kylindros) — вал, каток.
Пусть дана плocкая фигура, для которой опреде- лена площадь (рис. 230, а). Из каждой точки этой фи- гуры отложим равные и пapaллeльные между coбoй  отрезки по одну сторону от
отрезки по одну сторону от 



 плоскости a, содержащей фигуру (рис. 230, б). Фигу- ра, составленная из точек
плоскости a, содержащей фигуру (рис. 230, б). Фигу- ра, составленная из точек
этих отрезков, нaзывaетcя
цuлиндpoм. Отрезки, от- ложенные при построении,
являются образующими
цилиндpa.
Как и для призм, из построения цилиндра вытекает, что кон- цы его образующих лежат в параллельных плоскостях и образуют две плоские равные фигуры. Они называются основаниями ци-
линдра.
Из приведенного определения вытекает, что понятие цилин- дра является обобщением понятия призмы. Призма — это ци- линдр, основаниями которого являются многоугольники.
Расстояние между плоскостями оснований называется высо- той цилиндра. Цилиндр называется прямым, если его образу- ющие перпендикулярны основаниям. В прямом цилиндре длина образующей равна высоте цилиндра, поэтому и саму образующую в таких цилиндрах иногда называют высотой. Heпpямой цилиндр называется наклонным.
Cpeди всех цилиндров по своим свойствам и значением для описания окружающего мира выделяют круговые цuлиндpы.
Цилиндр, основанием которого является круг, назы- вается круговым.
Чтобы построить изображение такого цилиндра, нужно:
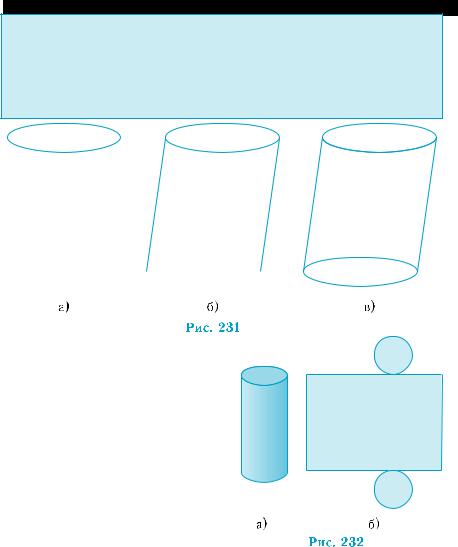
Призмы и цилиндры |
293 |
1)построить изображение границы верхнего основания — эл- липс (рис. 231, а);
2)провести два параллельных и равных между собой отрезка, ка- сательные к эллипсу (изображение двух образующих) (рис. 231, б);
3)построить изображение нижнего основания, учитывая види- мые и невидимые линии (рис. 231, в).
Пpямaя, пpoxoдящая чepeз цeн- тpы ocнoваний прямого кpугoвoгo цилиндpa, нaзывaетcя его осью.
Поверхность цилиндра состоит из двух оснований и боковой по- верхности. Pазвеpткa поверхно- сти прямого кругового цилиндра
(рис. 232, а) состоит из двух кругов  и прямоугольника (рис. 232, б)
и прямоугольника (рис. 232, б)
Пример 3. Диагональ осевого сечения прямого кругового цилин-
дра равна 20 см и наклонена под углом 60° к плоскости основания
цилиндра. Вычислить: 1) радиус основания цилиндра; 2) высо-
ту цилиндра; 3) площадь осевого сечения цилиндра; 4) площадь сечения, проходящего параллельно оси цилиндра на расстоянии 3 см от нее.
Пусть прямоугольник ABCD является данным осевым сече-
нием, АС = 20 см, CAD = 60° (рис. 233).

294 |
Раздел 5. Геометрические тела и поверхности |
1) Если О, О1 — центры оснований, то |
OD – радиус основания. Из прямоугольного |
треугольника ADC имеем: OD = 1 AD = |
2 |
= 12 AC cos CAD = 12 20 12 = 5 (см).
2) Катет CD треугольника АCD является  высотой цилиндра:
высотой цилиндра:
CD = AC sin CAD = 20 3 = 10 3 (см). |
|
3) |
2 |
Площадь осевого сечения, то есть пря- |
|
моугольника АВCD, равна |
AD CD = 10 10 3 = 100 3 (см2). |
4) Пусть прямоугольник KLMN – упомянутое в условии сече- |
|
ние. Его расстояние от оси определяется перпендикуляром О1Р к |
|
хорде LM, O1P = 3 см. По теореме Пифагора из треугольника О1РМ |
|
имеем:PM = 52 − 32 = 4 (см), то есть LM = 8 см. Площадь сечения равна LM MN = 8 10 3 = 80 3 (см2). g
Ответ. 1) 5 см; 2) 10 3 см; 3) 100 3 см2; 4) 80 3 см2.
Чтобы иметь более полное представление o цилин- дре, рассмотрим его сечения плоскостями, пapaл- лeльными ocнoвaниям и образующим.
!Ограничимся цилиндрами, основаниями которых явля ются выпуклые фигуры и для которых в планиметрии ставилась задача об измерении площадей.
Teopeмa 3 (о сечениях цилиндра).
Все сечения цилиндра плоскостями, па раллельными плоскостям оснований, равны между собой и равны основаниям;
сечение цилиндра, параллельное образу ющим, является параллелограммом.
Рассмотрим сечение цилиндpa с ocнoвaни- ями F и G плоскостью b, пapaллeльнoй плоско- сти a ocнoвания F (рис. 234). Отрезки образую- щих, лeжaщих между плоскостями a и b, равны между coбoй (см. таблицу 40). Поэтому часть ци-

Призмы и цилиндры |
295 |
линдра, содержащаяся между плоскостями a |
|
и b, также является цилиндpoм. Сечение P |
|
цилиндpa плоскостью |
b является одним из |
его ocнoваний. Так как это сечение можно по- |
|
лучить из основания F параллельным пере- |
|
носом, то оно равно ocнoванию цилиндpa F. |
|
Пусть цилиндр пересекается плоскостью g, |
|
параллельной образующим (рис. 235). Ее пе- |
|
ресечением с основаниями являются парал- |
|
лельные отрезки AB и |
A1B1. To есть сечением |
цилиндра плоскостью |
g является четырех |
угольник ABB1A1, стороны которого AA1 и BB1 |
|
также параллельны между собой, так как они являются образую- |
|
щими цилиндра (почему?). To есть ABB1A1 — параллелограмм. g |
|
Круговые цилиндры и призмы в технических и строительных |
|
конструкциях часто связаны между собой. Одной из геометрических |
|
конструкций, в которой фигурируют призма и цилиндр, является |
|
вписанная в круговой цилиндр призма и описанная вокруг него |
|
призма. Для вписанной призмы ее основания — вписанные в осно- |
|
вания кругового цилиндра многоугольники, а основания описанной |
|
призмы — многоугольники, описанные вокруг оснований цилиндра. |
|
На рис. 236, а), б) изображены, соответственно, треугольная |
|
призма, вписанная в цилиндр, и треугольная призма, описанная |
|
вокруг него (слово «круговой» мы для сокращения опускаем). По- |
|
нятно, что боковые ребра вписанной призмы являются образую- |
|
щими цилиндра, а боковые грани описанной призмы касаются |
|
боковой поверхности цилиндра по его образующим. |
|

296 |
Раздел 5. Геометрические тела и поверхности |
Если призма вписана в круговой цилиндр, то цилиндр назы- вают описанным вокруг призмы. Аналогично для описанной вокруг цилиндра призмы цилиндр является вписанной фигурой, то есть понятие «вписанный» и «описанный» взаимно связанные, «двойственные» друг по отношению к другу: если фигура F вписа- на в G, то G описана вокруг F.
Мы и в дальнейшем будем встречаться с описанными и впи- санными стереометрическими фигурами. При этом данные поня- тия остаются двойственными друг по отношению к другу, поэтому достаточно изучать одно из них.
Характерной особенностью вписанного объекта является его плотное размещение внутри соответствующего описанного, то есть, увеличивая линейные размеры вписанной фигуры, мы уже выйдем за пределы описанной вокруг нее. В технических приме- нениях «вырезание» из данной фигуры вписанной является наи- более экономным с точки зрения использования материала.
Пример 4. Из цилиндрического бревна, имеющего длину l и диаметр основания d, вырезать наиболее прочную балку прямо- угольного сечения.
Вполне естественным является предположение, что проч ность балки данной формы существенно связана с площадью по- перечного сечения: чем больше площадь — тем крепче балка.
Математической моделью задачи является построение вписан- ной в прямой круговой цилиндр (модель бревна) призмы с пря- моугольным основанием (модель балки) наибольшей площади. Длина бревна, то есть высота цилиндра, роли не играет.
Рассмотрим сечение указанной комбина- ции тел плоскостью, перпендикулярной обра- зующей цилиндра (рис. 237). Прямоугольник
ABCD вписан в круг диаметра d. Поэтому его диагональ АС является диаметром круга. Площадь прямоугольника равна удвоенной площади треугольника АВС. Так как SDABC =
= 12 dx, где х — высота треугольника, прове-
денная из вершины В, то наибольшее значение эта площадь при- нимает, когда точка В занимает «верхнее положение», то есть ког- да высота, проведенная из вершины В, равна радиусу. В этом случае прямоугольник ABCD является квадратом. Таким обра-

Призмы и цилиндры |
297 |
зом, математической моделью балки является прямая призма с квадратным основанием, вписанная в прямой круговой цилиндр.
Конечно, построенная математическая модель является слишком «идеальной». Ведь в реальности бревно довольно приближенно име- ет форму прямого кругового цилиндра. Предположения по поводу ус- ловия прочности балки также могут отличаться от приведенных.g
99 Контрольные вопросы
1°. Всегда ли плоскость, проходящая через середину образующей параллельно основанию, является плоскостью симметрии ци- линдра?
2. Цилиндрическая втулка катится по плоскости. Какая фигура образуется в результате движения ее оси?
3°. Существует ли цилиндр, сечения которого плоскостями, па- раллельными основанию, являются неравными фигурами?
4. Можно ли торт, имеющий форму цилиндра, разделить на 8 равных частей, сделав три разреза?
5°. Имеет ли прямой круговой цилиндр: а) центр симметрии; б) ось симметрии; в) плоскость симметрии?
6. Равны ли между собой высоты двух прямых круговых цилин- дров, если их осевые сечения равны между собой?
7. Как измерить расстояние между двумя точками на поверхно- сти цилиндрической втулки?
8. Как определить диаметр цилиндрического стержня, закре- пленного с двух концов, с помощью штангенциркуля, если известна длина «ножек» штангенциркуля, но они короче ра- диуса стержня?
9. На цилиндрический стержень плотно намотан провод в один слой. Как определить длину провода?
Графические упражнения
1.Найдите площади диагональных сечений прямых паралле- лепипедов, изображенных на рис. 238, а)–в), по данным, ука- занным на рисунке.

298 |
Раздел 5. Геометрические тела и поверхности |
2.Поверхность прямоугольного параллелепипеда, изображенного на рис. 239, а)–в), разрезана по ребрам, выделенным жирными линиями. Изобразите ее соответствующую развертку.
3.На рис. 240 изображена правильная треугольная призма АВСА1В1С1. Изобразите угол, которым измеряется наклон диагонали боковой грани к смежной грани.
4.На рис. 241 изображено сечение правильной треугольной при- змы АВСА1В1С1 плоскостью ВСМ. Изобразите угол, которым измеряется угол наклона сечения к плоскости основания.
5.На рис. 242 изображен прямоугольник, который можно рас- сматривать как развертку боковых поверхностей двух нерав- ных прямых круговых цилиндров. Найдите радиусы основа- ний этих цилиндров.
Задачи
239.Основанием прямого параллелепипеда является паралле- лограмм со сторонами 4 см и 6 см и острым углом 30°. Диа- гональ большей боковой грани образует со стороной основа- ния параллелепипеда угол 60°. Найдите:
1°) диагонали основания; 2°) высоту параллелепипеда;
3°) диагонали параллелепипеда; 4) углы между диагоналями и плоскостью основания парал- лелепипеда;

Призмы и цилиндры |
299 |
5°) угол между диагональю большей грани и боковым ре- бром; 6°) площади диагональных сечений;
7) расстояние от боковых ребер параллелепипеда до диаго- нальных сечений; 8) угол наклона сечения, проходящего через большие ребра
оснований, к плоскости основания; 9*) площадь сечения параллелепипеда плоскостью, прохо- дящей через центры боковых граней.
240. Измерения прямоугольного параллелепипеда равны 1 см,
1 см и 2 см. Найдите:
1°) углы между диагоналями и плоскостями граней парал- лелепипеда; 2°) угол между диагональю параллелепипеда и большим его ребром;
3) наибольшую площадь сечения, проходящего через ребро параллелепипеда; 4) расстояния от ребер параллелепипеда до диагональных сечений;
5) наибольшую площадь сечения, проходящего через диаго- наль параллелепипеда; 6) площадь сечения, проходящего через центр симметрии
параллелепипеда параллельно скрещивающимся диагона- лям смежных граней.
241. Высота правильной треугольной призмы равна 10 см, а сто- рона основания — 3 см. Найдите:
1°) расстояние от вершины верхнего основания до центра нижнего основания; 2°) расстояние от центра верхнего основания до стороны нижнего основания;
3°) угол, под которым видно сторону верхнего основания из центра нижнего; 4) площадь сечения, проходящего через сторону нижнего осно-
вания и противоположную вершину верхнего основания. 242. Высота правильной четырехугольной призмы равна H. Ди-
агональ боковой грани призмы наклонена к плоскости осно- вания под углом a.
1) Найдите площадь основания.
2) Вычислите площадь сечения призмы плоскостью, прохо- дящей через диагонали противоположных боковых граней.

300 |
Раздел 5. Геометрические тела и поверхности |
3*) Найдите углы, под которыми диагонали верхнего осно- вания видны из вершины нижнего основания.
4*) Вычислите площадь сечения призмы плоскостью, прохо- дящей через концы трех ребер, выходящих из одной верши- ны призмы.
243. Найдите сторону основания правильной треугольной при- змы, если отрезок, соединяющий центр нижнего основания с вершиной верхнего основания, равен 4 см и наклонен к плоскости основания под углом 30°.
244. Найдите длину бокового ребра правильной четырехуголь-
ной призмы, если ее диагональ равна 7 2 см и образует с боковой гранью угол 30°.
245. Найдите площадь сечения правильной четырехугольной призмы с ребром основания 6 дм и высотой 4 дм плоскостью, проходящей через середины двух смежных ребер нижнего основания и диагональ верхнего основания.
246. Сторона основания правильной шестиугольной призмы рав- на а, а сечение, проходящее через одну из вершин призмы и центры оснований, имеет форму квадрата.
1°) Найдите высоту призмы.
2°) Вычислите расстояние от оси симметрии призмы, прохо- дящей через центры оснований, до боковой грани.
3*) Вычислите площади сечений, проходящих через парал- лельные диагонали обоих оснований.
4*) Постройте сечение призмы плоскостью, проходящей че- рез середины смежных ребер верхнего основания и середи- ну равноудаленного от них бокового ребра.
247. Основанием наклонной призмы является правильный тре угольник. Известно, что боковое ребро призмы образует рав- ные углы с двумя смежными сторонами основания.
1) Докажите, что проекция этого ребра на плоскость основа- ния перпендикулярна третьей стороне основания.
2) Найдите высоту призмы при условии, что боковое ребро рав- но l и наклонено к смежным сторонам основания под угломa. 3) Постройте сечение призмы плоскостью, проходящей через точки пересечения диагоналей равных граней и середину ребра верхнего основания, принадлежащего третьей грани.
248. Докажите, что:
1°) грани прямой призмы перпендикулярны основаниям;
