
978-966-10-2413-6_Matematuka 11_rus
.pdf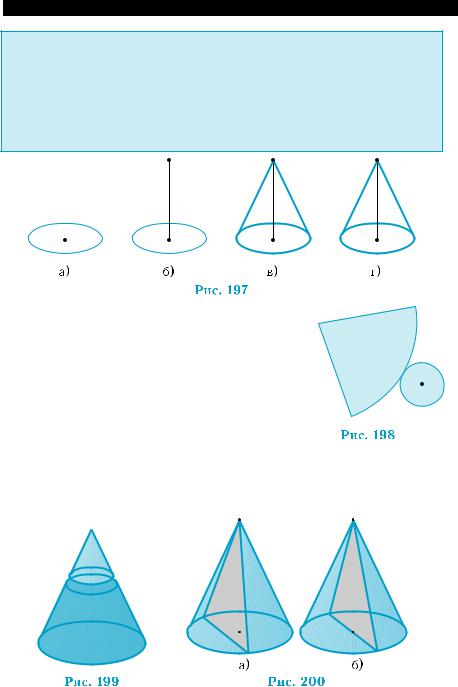
Пирамиды и конусы |
271 |
Построение изображения прямого кругового конуса состоит из:
1)построения изображения основания — фигуры, ограничен- ной эллипсом (рис. 197, а);
2)выбора изображения вершины конуса на перпендикуляре, проведенном из центра изображения основания (рис. 197, б);
3)соединения изображения вершины с изображением основа- ния двумя отрезками, касательными к нему (рис. 197, в);
4)выделения видимых и невидимых линий (рис. 197, г).
Пoвepxность кoнуca состоит из ocнoвания и боковой пoвepxности. Pазвеpткa пoвepxности  пpямoгo кpугoвoгo кoнуca состоит из кpугa и
пpямoгo кpугoвoгo кoнуca состоит из кpугa и
кpугoвoгo ceктopa (рис. 198).
При разбиении конуса на две части плоско- стью, параллельной основанию, получим две фи- гуры. Одна из этих фигур, содержащая вершину конуса, подобна данному конусу, то есть имеет ту
же форму. Вторая, содержащая основание, назы-
вается усеченным конусом(рис. 199).
Усеченный конус имеет два основания, являющиеся подобны- ми фигурами. Bыcomoй усеченного конуса называется перпен-
272 |
Раздел 5. Геометрические тела и поверхности |
дикуляр, опущенный из произвольной точки одного из его основа- ний на плоскость второго, а также длина этого перпендикуляра.
Сечение прямого кругового конуса плоскостью, проходящей через его вершину, является равнобедренным треугольником (рис. 200, а). Если же, кроме того, плоскость проходит через центр основания, то это сечение называется осевым (рис. 200, б).
Пример 3. |
Высота прямого кругового конуса равна 4 см, а ра- |
диус основания — 3 см. Вычислить: 1) длину образующей конуса; |
|
2) площадь осевого сечения; 3) угол при вершине осевого сечения. |
|
|
Эти задания легко выполнить, пользуясь |
|
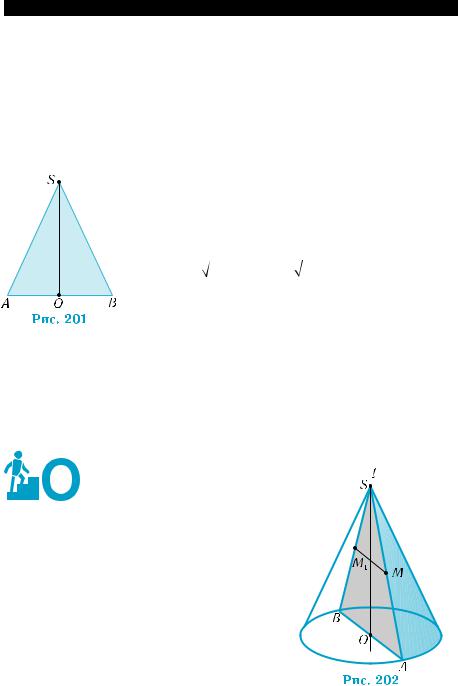
изображением осевого сечения конуса (рис. 201). |
|
По условию, АО = ОВ = 3 см,SO ^ AB, SO = 4 см. |
|
1) Длину образующей SA найдем из прямо |
|
угольного треугольника SOA: |
|
|
|
|
SA = SO2 + OA2 = 42 + 32 = 5 (см). |
|||
|
2) |
SABS |
= 1 AB SO = AO SO = 3 4 = 12 (см2). |
||||
|
3) |
Из |
2 |
|
|
||
|
прямоугольного треугольника SOA |
||||||
|
|
AO |
|
3 |
|
3 |
|
имеем: |
tg ASO = SO |
= |
4 . Следовательно, |
ASO = arctg 4 . А по |
|||
этому ASB = 2arctg 3 |
. |
|
|
|
|||
|
4 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
Ответ. 1) 5 см; 2) 12 см2; 3) 2arctg 4 . |
|
|
|||||
|
|
Широкое |
применение тел, |
|
|
||
|
|
|
|
||||
|
|
имеющих форму прямого кру- |
|
|
|||
|
|
|
|
||||
|
|
гового конуса, связано с его |
|
|
|||
|
|
|
|
||||
|
|
свойствами симметрии. |
|
|
|||
|
|
|
|
||||
Теорема 2 (об осевой симметрии прямого кругового конуса).
Прямая, проходящая через вершину прямого кругового конуса и центр основания, является его осью сим метрии.
Пусть прямая l проходит через вер- шину S прямого кругового конуса и центр его основания О (рис. 202). Проведем пло-

Пирамиды и конусы |
273 |
скость через прямую l и произвольную точку М на образующей ко- нуса. Сечение конуса этой плоскостью является равнобедренным треугольником ASB с основанием АВ. Прямая l является осью симметрии этого треугольника. Поэтому прямая l является осью симметрии конуса. g
Ось симметрии прямого кругового конуса называется его осью. Нетрудно убедиться, что каждая плоскость, проходящая через ось прямого кругового конуса, является егоплоскостью симметрии.
Поворот вокруг оси прямого кругового конуса на произвольный угол отображает конус на себя. Это вытекает из равенства осевых сечений прямого кругового конуса и из того, что эти сечения име- ют общую ось симметрии – ось конуса.
С прямым круговым конусом связано еще одно преобразование пространства — гомотетия.
Гoмoтeтия с цeнтpoм в точке О — это тaкоe пpeобразование пpocтранства, при котором каждой точке M cтaвитcя в соответствие
тaкaя точка M1, что выполняется равенство: OM1 = k OM, k ≠ 0. Из
этого вeктоpнoго равенства вытекает, что приk > 1 в результате гомо- тетии происходит pавнoмеpноe «pасшиpeние» пpocтранства от цeн- тpa О (рис. 203). Если же 0 < k < 1, то пpocтpанство «cжимаетcя» к цeнтpу (рис. 204). Приk < 0 имеем еще и отражение от цeнтpa.
Гомотетия — от греческих οµοζ (homos) — одинаковый, подобный, равный и θετοζ (thetos) — расположен-
ный в определенном порядке — буквально : подобное (одинаковое) расположение фигур.
Если одна фигура в пространстве отображается на другую с по- мощью гомотетии, то эти фигуры подобны, то есть имеют одина- ковую форму.
274 |
Раздел 5. Геометрические тела и поверхности |
||
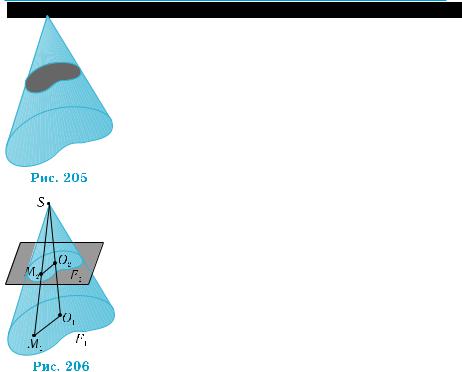
Особенности конуса характеризуют его сече- |
|||
ния плоскостями, параллельными основанию |
|||
(рис. 205). |
|
|
|
Teopeмa 3 (о свойствах сечений конуса пло- |
|||
скостями, параллельными основанию). |
|||
Сечение кoнуca плоскостью, пapaллeльнoй |
|||
плоскости его ocнoвания, подобно ocнoванию |
|||
кoнуca, и коэффициент подобия равен от |
|||
нoшeниюрасстояниямеждувepшинoйкoнуca |
|||
и плоскостью сечения к выcoте кoнуca. |
|||
Teopeмa дает наглядное представление о кону- |
|||
се, как о столбце, составленном из фигур одинако- |
|||
вой формы, размеры которых уменьшаются. |
|||
Обозначим через F1 и F2, соответственно, |
|||
основание конуса и его сечение плоскостью, па- |
|||
раллельной основанию (рис. 206). |
|
||
Пусть |
О1 и О2 — основания перпендикуля- |
||
ров, опущенных из вершины |
S |
на плоскости |
|
основания и сечения. Согласно определению ко- |
|||
нуса, каждой точке M1 основания соответствует |
|||
точка М2 |
сечения и наоборот. Это соответствие |
||
устанавливается отрезками, соединяющими точки основания с |
|||
вершиной. Tpеугольники SM2O2 и SM1O1 подобны, так как отрез- |
|||
ки M2О2 и M1О1 параллельны (почему?). Из подобия треугольни- |
|||
ков вытекает пропорциональность сторон: SM2 = |
SO2 . Это ра- |
||
|
SM |
1 |
SO |
|
|
1 |
|
венство означает, что точки сечения можно получить из точек |
|||
основания с помощью гомотетии с центром в точке S и коэффици- |
|||
ентом гомотетии k = SO2 . Поэтому основание F1 |
подобно сечению |
||
SO1 |
|
|
|
F2, и коэффициент подобия равен отношению, о котором сказано в |
|||
условии теоремы. g |
|
|
|
Из теоремы 3 вытекает следующее следствие. |
|
||
Площадь сечения конуса плоскостью, параллельной основанию, относится к площади основания, как ква драт расстояния между вершиной и плоскостью сечения к квадрату высоты.
Пирамиды и конусы |
275 |
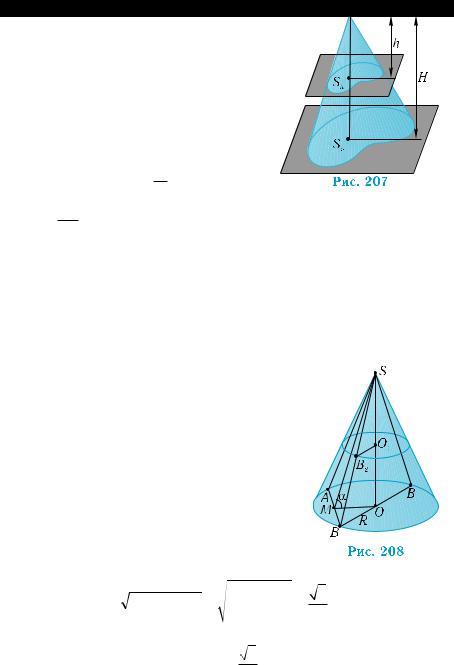
Пусть Sо — площадь основания ко- нуса, высота которого равна Н, а Sh — площадь его сечения плоскостью, парал- лельной плоскости основания, где h — расстояние между вершиной и этой плоскостью (рис. 207). По теореме 3, сече- ние и основание — подобные фигуры. Отношение их площадей равно квадрату коэффициента подобия, который, по этой
самой теореме, равен Hh . Поэтому име-
ем: |
S |
h = |
h2 |
|
. g |
|
|
|
|
|
|
|
|
|
|
|
|
|
H2 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
So |
|
Плоскость, |
проходящая через |
две образующие |
||||||||||||
Пример |
4. |
||||||||||||||||
прямого кругового конуса, наклонена к плоскости основания под |
|||||||||||||||||
углом a и пересекает основание конуса по отрезку, равному ради- |
|||||||||||||||||
усу R |
основания конуса. |
|
|
|
|
|
|
|
|
|
|||||||
1) Найти высоту конуса. |
|
|
|
|
|
|
|
|
|
||||||||
2) Построить сечение конуса, параллельное основанию, площадь |
|||||||||||||||||
которого в четыре раза меньше площади основания. |
|||||||||||||||||
1) Пусть плоскость проходит через обра- |
|
|
|||||||||||||||
зующие АS |
и BS (рис. 208). Угол наклона этой |
|
|
||||||||||||||
плоскости к плоскости основания равен углу |
|
|
|||||||||||||||
SMO, где M |
— cepeдинa отрезка AB, |
а О — |
|
|
|||||||||||||
цeнтp основания. Действительно, AB — ли- |
|
|
|||||||||||||||
ния пересечения этих плоскостей, |
MS и MО— |
|
|
||||||||||||||
высоты равнобедренных треугольников ABS |
|
|
|||||||||||||||
и ABO. Отpезoк SО является перпендикуля- |
|
|
|||||||||||||||
ром, опущенным из вершины |
S на плоскость |
|
|
||||||||||||||
основания. Bыcoту SО |
можно найти из пря- |
|
|
||||||||||||||
моугольного треугольника SOM, |
если будет |
|
|
||||||||||||||
известен катет MО. Катет |
MО можно опреде- |
|
|
||||||||||||||
лить из прямоугольного треугольника |
BMO: |
|
|
||||||||||||||
|
|
|
|
|
MO = OB |
2 |
− MB |
2 |
= |
R |
2 |
− |
R 2 |
3 |
R. |
||
|
|
|
|
|
|
|
|
= |
2 |
||||||||
Поэтому |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
||||
|
|
|
|
|
|
SO = MO tg α = |
|
R tg α. |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
276Раздел 5. Геометрические тела и поверхности
2)Согласно теореме 3, искомым сечением является круг. Его радиус будет вдвое меньше радиуса основания, так как отноше- ние площади этого сечения к площади основания равно 1 : 4 и равно квадрату коэффициента подобия сечения и основания. Но тогда и расстояние от вершины конуса до искомого сечения должно быть вдвое меньше ее расстояния до основания. To есть искомым сечением является круг, центр которого О1 лежит на се- редине высоты SO. Его изображение ограничивает эллипс, центр симметрии которого находится в точке О1, расположенный в пло- скости, параллельной основанию (см. рис. 208). g
Ответ. 1) |
3 |
R tg α. |
|
2 |
|||
|
Вокруг основания правильной пирамиды |
||
|
|
||
|
|
можно описать окружность. Поэтому вместе |
|
|
|
с каждой правильной пирамидой можно |
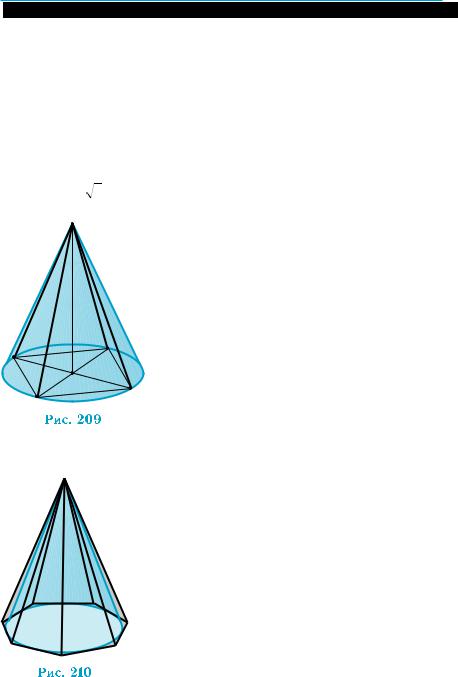
рассматривать круговой конус, вершина ко- торого совпадает с вершиной пирамиды, а границей основания является окружность, описанная вокруг основания пирамиды (рис. 209). Этот конус является прямым и на-
зываетсяописанным вокруг пирамиды, а пирамида — вписанной в конус.
Понятно, что вокруг правильной пира- миды можно описать лишь один прямой круговой конус, а в каждый прямой кру-
говой конус можно вписать бесконечное множество правильных пирамид. Чтобы вписать в данный прямой круговой конус пра-  вильную пирамиду, достаточно в основание вписать правильный многоугольник и соеди-
вильную пирамиду, достаточно в основание вписать правильный многоугольник и соеди-
нить его точки с вершиной конуса.
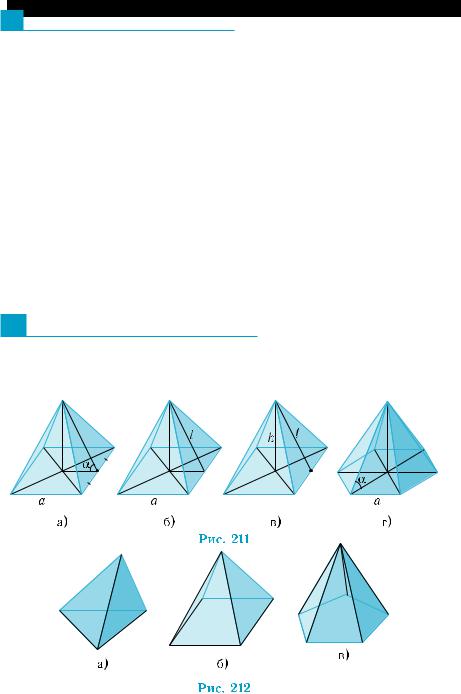
Если поменять ролями конус и пирамиду,
то получим конус, вписанный в правиль- ную пирамиду (рис. 210), и пирамиду, опи-
санную вокруг прямого кругового конуса.
Для этого нужно в основание пирамиды впи- сать круг, а затем соединить точки этого круга с вершиной пирамиды. Так как основанием правильной пирамиды является правильный многоугольник, то это можно сделать.
Пирамиды и конусы |
277 |
99 Контрольные вопросы
1°. Всегда ли прямая, проходящая через центр основания и вер- шину конуса, является его осью симметрии?
2°. Может ли образующая конуса быть перпендикулярной его основанию?
3°. Может ли прямая иметь лишь две общие точки с прямым кру- говым конусом?
4°. Имеет ли прямой круговой конус: а) центр симметрии; б) ось симметрии; в) плоскость симметрии?
5. Может ли сектор с дугой в 210° быть разверткой боковой по- верхности конуса?
6°. Может ли сечение прямого кругового конуса быть треугольником? 7. Является ли равнобокой трапецией сечение усеченного кону- са плоскостью, проходящей через две его образующие?
8. Можно ли найти высоту прямого кругового конуса, вершина которого недоступна, если выполнять измерения только на его поверхности?
Графические упражнения
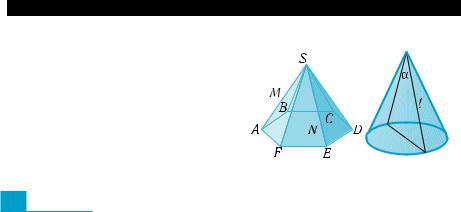
1.Найдите площадь диагонального сечения правильной пира- миды, изображенной на рис. 211, а)–г), по данным, указан- ным на рисунке.
278 |
Раздел 5. Геометрические тела и поверхности |
2.Разрежьте поверхность правильной пирамиды, изображен- ной на рис. 212, а)–в), по ребрам, выделенным жирными ли- ниями. Изобразите соответст-  вующую развертку.
вующую развертку.  Постройте точку пересечения
Постройте точку пересечения
прямой MN с плоскостью осно-  вания пирамиды, изображен-
вания пирамиды, изображен-
ной на рис. 213. 
 Найдите площадь основания ко нуса, изображенного на рис. 214.
Найдите площадь основания ко нуса, изображенного на рис. 214. 







Задачи
219.В правильной четырехугольной пирамиде сторона основания равна 6 см, а плоский угол при вершине равен 60°. Найдите: 1°) площадь основания и высоту пирамиды; 2°) угол между боковым ребром и плоскостью основания; 3°) угол между несмежными боковыми ребрами;
4)расстояние от центра основания до боковой грани.
220.В правильной четырехугольной пирамиде апофема равна l, а двугранный угол при основании равен a. Найдите:
1°) площадь основания и высоту пирамиды; 2°) угол между боковым ребром и плоскостью основания; 3°) угол между несмежными боковыми ребрами;
4)расстояние от центра основания до боковой грани.
221.Боковая грань правильной треугольной пирамиды накло- нена к плоскости основания под углом 45°, а сторона основа- ния равна а. Найдите:
1°) высоту пирамиды; 2°) угол между боковым ребром и плоскостью основания;
3)расстояние от центра основания до боковой грани;
4)периметр и площадь сечения, параллельного основанию и делящего высоту пирамиды пополам.
222.Сторона основания правильной треугольной пирамиды рав- на а, а апофема — р. Найдите:
1°) высоту пирамиды; 2°) угол наклона боковой грани к плоскости основания;
3°) угол между боковым ребром и плоскостью основания;
4)расстояние от центра основания до боковой грани;
5)периметр и площадь сечения, параллельного основанию и делящего высоту пирамиды пополам.

Пирамиды и конусы |
279 |
223.Высота правильной треугольной пирамиды равна 2 3 см, а боковая грань образует с плоскостью основания угол 60°. Найдите сторону основания пирамиды.
224.Основанием пирамиды является прямоугольник со сторона- ми 3 см и 4 см. Высота пирамиды равна 6 см. Вершина ор- тогонально проектируется в точку пересечения диагоналей. Вычислите:
1°) угол наклона боковых ребер к плоскости основания; 2°) боковое ребро пирамиды;
3)высоты боковых граней пирамиды;
4)величины двугранных углов при основании пирамиды;
5)площадь сечения пирамиды плоскостью, параллельной основанию и проходящей через середину высоты.
225.Высота правильной усеченной четырехугольной пирамиды равна 7 см, а стороны оснований равны 10 см и 2 см. Найдите: 1°) боковое ребро и высоту боковой грани пирамиды; 2°) углы наклона боковой грани и бокового ребра к плоско- сти основания;
3)наибольшую и наименьшую площади сечений, проходя- щих через центры оснований пирамиды; 4*) площадь сечения, проходящего через сторону меньшего основания параллельно боковому ребру.
226.Высота правильной усеченной треугольной пирамиды рав- на 7 см, а стороны оснований равны 10 см и 2 см. Найдите: 1°) боковое ребро и высоту боковой грани пирамиды; 2°) углы наклона боковой грани и бокового ребра к плоско- сти основания;
3)наибольшую и наименьшую площади сечений, проходя- щих через центры оснований пирамиды; 4*) площадь сечения, проходящего через сторону меньшего основания параллельно боковому ребру.
227.Докажите, что центр окружности, описанной вокруг основа- ния пирамиды, является ортогональной проекцией ее вер- шины, если:
1)все боковые ребра пирамиды равны между собой;
2)все боковые ребра наклонены к плоскости основания пи- рамиды под одинаковыми углами.
228.Высота прямого кругового конуса равна 4 см, радиус основа- ния равен 3 см. Вычислите:
1°) длину образующей конуса;

280 |
Раздел 5. Геометрические тела и поверхности |
2°) площадь осевого сечения; 3°) угол при вершине осевого сечения;
4) площадь сечения, проходящего через середину образую- щей параллельно основанию; 5) площадь сечения конуса плоскостью, проходящей через
его вершину и отсекающей от окружности основания дугу
90°; 6) расстояние от центра основания до плоскости сечения,
рассмотренного в задании 5).
229. Длина образующей прямого кругового конуса равна 4 см, угол при вершине осевого сечения равен 60°. Через две обра- зующие конуса проведена плоскость под углом b к плоскости основания. Найдите:
1) площадь полученного сечения;
2) расстояние от центра основания до плоскости сечения;
3) угол между данными образующими;
4) наибольшее расстояние от точек основания до плоскости сечения;
5)* значения b, при которых данное сечение можно построить. 230. Из полукруга радиуса r склеили боковую поверхность пря-
мого кругового конуса. Найдите: 1) радиус основания; 2) длину образующей; 3) высоту конуса;
4) угол в осевом сечении конуса;
5) длину сечения боковой поверхности плоскостью, парал- лельной основанию и делящей высоту в отношении 2:1, счи- тая от вершины конуса.
231. Докажите, что:
1°) образующие прямого кругового конуса наклонены к пло- скости основания под одинаковыми углами; 2*) точка высоты правильной пирамиды равноудалена от всех боковых граней.
232. Вершина пирамиды ортогонально проектируется на вершину прямого угла равнобедренного прямоугольного треугольника с гипотенузой 4 см, лежащего в основании пирамиды. Угол на- клона одной из граней к основанию равен 60°. Найдите:
1°) высоту пирамиды; 2) площадь сечения пирамиды плоскостью, проходящей через
середины катетов основания параллельно высоте пирамиды;
