
Yuriy Kruglyak. Quantum Chemistry_Kiev_1963-1991
.pdfSλ pq = ∞∫du u2 Rλ p (u)Rλq (u),
0
Uλ pq = ∞∫du u Rλ p (u)Rλq (u),
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
= 1 |
∞ du u2 |
dRλ p (u) |
|
dRλq (u) |
+λ(λ +1)R |
|
(u)R |
(u) |
, |
|
|
|
(8) |
||||||||||
|
|
|
|
|
|
|||||||||||||||||||
λ pq |
2 |
∫0 |
|
|
|
du |
|
du |
|
|
|
|
λ p |
|
λq |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ν |
|
∞ |
|
−ν +1 |
u |
|
ν +2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Iλ pq,µrs = ∫du u |
|
|
|
∫dv v |
Rλ p (u)Rλq (u)Rµr (v)Rµs (v) + Rλ p (v)Rλq (v)Rµr (u)Rµs (u) , |
|
||||||||||||||||||
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ν |
|
1 |
∞ |
|
|
−ν +1 u |
|
ν +2 |
Rλ p (u)Rµr (u)Rλq (v)Rµs (v) + Rλq (u)Rµs (u)Rλ p (v)Rµr (v) + |
|||||||||||||||
Kλ pq,µrs |
= 2 |
∫du |
u |
|
∫dv v |
|
|
+R (u)R (u)R (v)R (v) + R (u)R (u)R (v)R (v) |
|
|||||||||||||||
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
λ p |
µs |
|
|
λq |
|
µr |
λq |
µr |
λ p |
µs |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Первые три формулы (8) определяют матричные элементы матриц |
|||||||||||||||||||||||
интегралов перекрывания |
|
Sλ (Sλ pp =1) |
|
и одноэлектронного гамильтониана без |
||||||||||||||||||||
учета взаимодействия между электронами |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H =T − zU. |
|
|
|
|
|
(9) |
||||
Квадратные матрицы, где собраны элементы, соответствующие определенной симметрии, обозначаются соответствующими индексами Sλ ,
Uλ ,Tλ , а полное собрание всех матричных элементов обозначается без индексов, как в (9). Все эти матрицы симметричны. В памяти компьютера хранятся только элементы, например, Sλ pq с p ≥ q в определенном порядке по
индексу λ . Например, для базисного набора из трех s- и двух p-функций матричные элементы хранятся в следующем порядке:
011, 021, 022, 031, 032, 033, 111, 121, 122, |
(10) |
так что соответствующая матрица имеет следующую индексную структуру
λp\λq |
01 |
02 |
03 11 |
12 |
|
01 |
011 |
|
|
|
|
02 |
021 |
022 |
|
(11) |
|
03 |
031 |
032 |
033 |
||
|
|||||
11 |
|
|
111 |
|
|
12 |
|
|
121 |
122 |
Записанные в виде (10) матричные элементы могут рассматриваться как элементы супервектора. В виде же (11) они образуют обычные матрицы.
Две последние формулы (8) образуют элементы суперматриц:
270
|
|
0 |
− |
1 |
λ+µ |
|
ν |
(12) |
|
Pλ pq,µrs = Jλ pq,µrs |
2 |
∑ |
Aλµν Kλ pq,µrs , |
||||||
|
|
|
|
ν =|λ−µ| |
|
|
|||
|
2(λ,µ)< |
ν |
|
|
|
1 |
λ+µ |
ν |
(13) |
Qλ pq,µrs = |
∑ |
Jλµν Jλ pq,µrs − |
2 |
∑ |
Kλµν Kλ pq,µrs . |
||||
|
ν =0 |
|
|
|
|
ν =|λ−µ| |
|
|
|
Эти элементы хранятся в следующем порядке:
|
λ pq\µrs 011 |
021 |
022 |
031 032 |
033 111 121 |
122 |
|||||
|
011 |
X |
|
|
|
|
|
|
|
|
|
|
021 |
X |
X |
|
|
|
|
|
|
|
|
|
022 |
X |
X |
X |
|
|
|
|
|
|
|
|
031 |
X |
X |
X |
X |
|
|
|
|
(14) |
|
|
032 |
X |
X |
X |
X |
X |
|
|
|
||
|
|
|
|
|
|||||||
|
033 |
X |
X |
X |
X |
X |
X |
|
|
|
|
|
111 |
X |
X |
X |
X |
X |
X |
X |
|
|
|
|
121 |
X |
X |
X |
X |
X |
X |
X |
X |
|
|
|
122 |
X |
X |
X |
X |
X |
X |
X |
X |
X |
|
В |
формулах |
(12) и |
(13) A , J и K – численные коэффициенты. |
||||||||
Коэффициенты Aλµν |
определяются формулой для произведения двух полиномов |
||||||||||
Лежандра: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
λ+µ |
|
|
|
|
|
|
|
|
Pλ (x)Pµ (x) = |
∑ |
(2ν +1)Aλµν Pν (x). |
|
(15) |
||||
|
|
|
|
|
|
ν =|λ−µ| |
|
|
|
|
|
Коэффициенты Jλµν и Kλµν |
– свои для каждого состояния и конфигурации |
||||||||||
атома. |
В случае |
одной |
открытой оболочки |
(λ = µ ), |
они неоднозначны, |
||||||
поскольку имеют смысл только комбинации Jλλν − |
1 Kλλν . Это позволяет вообще |
||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
избавиться от коэффициентов J в этом случае. Значения коэффициентов Kλµν |
|||||||||||
приведены в [31] для конфигураций s , |
pn и spn . Составлены и более обширные |
||||||||||
таблицы этих коэффициентов. |
|
|
|
только суперматрица P , а |
|||||||
В |
случае |
закрытой |
оболочки |
нужна |
|||||||
суперматрица Q |
позволяет учесть наличие открытой оболочки. |
||||||||||
Если не считать зависимость Q от коэффициентов Jλµν |
и Kλµν , то мы до |
||||||||||
сих пор нигде не использовали зависимости от чисел заполнения оболочек. Эта
271
зависимость включена в определение различных матриц плотности Dλ , которые
используются в итерационном процессе самосогласования. Эти матрицы строятся из ортонормированной системы векторов
C† |
S C |
jλ |
=δ |
ij |
|
(16) |
|||
iλ |
λ |
|
|
|
|
|
|||
согласно формуле |
|
|
|
|
|
|
|
|
|
D |
= N |
|
C C† |
, |
(17) |
||||
iλ |
|
|
iλ |
iλ |
|
iλ |
|
|
|
где Niλ – число заполнения оболочки |
|
iλ . |
Путем суммирования по i |
затем |
|||||
определяются матрицы плотности закрытых Dc и открытых Do оболочек, а также полная матрица плотности
Dt = Dc + Do , |
(18) |
которая имеет ту же самую индексную структуру (1), что и матрицы S и H . Теперь можно записать формулу для полной энергии, которая применима
для большого класса состояний, когда существует одна открытая оболочка для данного типа симметрии:
† |
t |
|
1 |
t† t |
|
1 |
o† o |
. |
(19) |
E = H |
D |
+ |
2 D |
PD |
− |
2 D |
QD |
Скалярные произведения в (19) определяются обычным путем между суперматрицами P или Q и между супервекторами вида (10). Конечно, предполагается полное суммирование по всем индексам. Недиагональные элементы матриц плотности должны быть умножены на двойку с тем, чтобы формула (19) давала правильный результат.
Уравнения ССП для векторов получаются применением вариационного принципа к энергии (19). Эти уравнения различны для векторов закрытой и открытой оболочек. Гамильтонианы ССП для закрытой и открытой оболочек в том случае когда не встречается закрытых и открытых оболочек одного типа симметрии имеют вид:
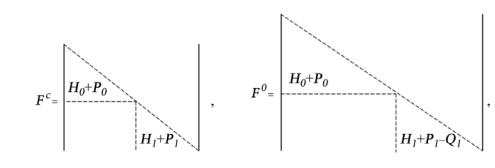
Fc = H + P , |
(20) |
Fo = H + P −Q , |
(21) |
где
t |
, |
(22) |
P = PD |
272
o |
. |
(23) |
Q = QD |
||
В расчетах атомов с конфигурацией 1s2 2s2 2 pn матрицы F c |
и Fo имеют |
|
следующий вид |
|
(24) |
где индексы 0 и 1 соответствуют s- и p-симметрии.
Соответствующие уравнения ССП |
|
FcC = εSC , |
(25) |
FoC = εSC |
(26) |
для закрытых и открытых оболочек являются задачами на псевдособственные значения и определяют вектора ciλ .
Для решения уравнений (25) и (26) был использован итерационный метод [31]. В этом методе каждый собственный вектор c и соответствующее ему собственное значение ε находятся последовательно исходя из приближенного исходного вектора c0 , который так или иначе необходимо задавать чтобы
посчитать матрицу гамильтониана в первый раз. Этот метод весьма эффективный, и трех – четырех итераций обычно достаточно доя сходимости. Метод совершенно общий и может быть применен всегда, когда нет необходимости искать все собственные векторы матрицы гамильтониана, а
нужны только некоторые из них. |
|
|
|
Запишем задачу на псевдособственные значения в виде |
|
|
Fc =ε Sc , |
(27) |
где |
F и S – данные симметричные матрицы, а c и ε нужно определить. Пусть |
|
c0 |
представляет приближенный собственный вектор, а δc |
есть поправка, |
которая делает из него действительный собственный вектор |
|
|
|
c = c0 +δc . |
(28) |
|
Без потери общности можно считать, что вектор c0 |
нормирован и |
ортогонален к δc , а именно: |
|
|
|
273 |
|
c†Sc =1, |
(29) |
|
0 |
0 |
|
c†Sδc = 0 . |
(30) |
|
0 |
|
|
Определим приближенное собственное значение
ε |
0 |
= c†Fc , |
(31) |
|
|
0 |
0 |
|
|
и пусть точное собственное значение ε отличается от приближенного ε0 на δε :
ε =ε0 +δε . |
(32) |
Подставляя c (28) и ε (32) в (27), умножая далее получившееся уравнение слева на c0† и используя (29) – (31), получаем
δε = c†Fδc = c†(F −ε |
0 |
S)δc . |
(33) |
|
0 |
0 |
|
|
|
Введем обозначения |
|
|
|
|
|
p0 = Sc0 , |
|
|
(34) |
q0 = (F −ε0S)c0 |
|
(35) |
||
и вновь подставим c и ε в (27), заменив значение δε согласно (33). При этом получим
(F −ε |
0 |
S)δc = −q +(q†δc) p +Ο |
(δc), |
(36) |
|||
|
0 |
0 |
0 |
2 |
|
|
|
где последний член – второго порядка по δc . Опуская последний член в (36) и добавляя – член, тождественно равный нулю в силу (30), получаем уравнение для δc , верное в первом порядке, а именно:
G0δc = −q0 , |
|
|
(37) |
|||
где симметричная матрица |
|
|
|
|
|
|
G = F −ε |
0 |
S − p q† |
−q p† . |
(38) |
||
0 |
0 |
0 |
0 |
0 |
|
|
Уравнение (37) подлежит дальнейшему анализу. Матрица G0 – особенная, |
||||||
поскольку, как легко установить, |
|
|
|
|
|
|
G0c0 = 0 . |
|
|
|
(39) |
||
Предполагается, что G0 не |
|
имеет |
|
других |
собственных векторов, |
|
соответствующих нулевому собственному значению. При этом уравнение (37)
274
имеет решения для δc тогда и только тогда, когда правая часть ортогональна к решению соответствующего однородного уравнения
q†c = 0, |
(40) |
|
0 |
0 |
|
что справедливо в нашем случае, поскольку (40) эквивалентно (31), причем решение для δc определяется с точностью до произвольного аддитивного вклада λ c0 . Среди множества этих решений выбирается то, которое
удовлетворяет условию (30). Практически сначала находим частное решение (37), а затем делаем его ортогональным к c0 , используя указанное свойство.
Уравнение (37) решается методом исключения Гаусса, причем существенно используется симметричность матрицы G0 . Фактически, от
матрицы G (в дальнейшем будем опускать индекс 0), так же как от матрицы F хранится в памяти компьютера, так что формально триангуляция матрицы G может быть описана заменой каждого элемента G элементом действительно
треугольной матрицы |
T . |
Элементы T |
последовательно вычисляются |
по |
|||||
следующей формуле: |
|
|
|
|
|
|
|
|
|
|
|
|
n−p−1 |
|
|
|
|
|
|
|
|
Tpq = Gpq − ∑ Tn−r,pTn−r,q |
/ Tn−r,n−r , |
|
|
|
(41) |
||
|
|
|
r=0 |
|
|
|
|
|
|
которая |
применяется |
для |
q ≤ p, 1 ≤ p ≤ n , |
если |
только |
считать сумму |
в |
(41) |
|
равной |
нулю для последнего ряда ( p = n, n – |
порядок |
матрицы). |
Мы |
таким |
||||
образом превращаем (37) в |
|
|
|
|
|
|
|
||
|
|
|
Tδc = −t , |
|
|
|
|
(42) |
|
причем |
формула, подобная (41), превращает |
q в t |
, так что |
нет |
нужды |
||||
рассматривать этот процесс отдельно – он может быть сделан как часть триангуляции.
Если бы T была неособенной матрицей, мы бы непосредственно решали (42). Первое уравнение давало бы δc1 , второе – δc2 и т. д. Но мы знаем, что задача имеет бесконечно много решений. Если мы ищем собственный вектор, у которого c1 ≠ 0, то ясно, что мы можем позволить произвольное значение для
δc1 . Это может быть только если T11 = t1 = 0 . Фиксируем этот произвол, положив
δc1 = 0 . Тогда можно посчитать δc2 из второго уравнения, δc3 из третьего и т. д.
Ясно, что в таким случае нам вообще не нужен первый столбец матрицы T . Поэтому удобно заменить с самого начала столбец матрицы G вектором q .
275
После триангуляции мы будем иметь нужную часть T и вектор t в качестве первого столбца этой матрицы.
Определив таким образом поправку δc′, которая удовлетворяет (42) и для
которой δc1′ = 0 , мы получим затем искомый поправочный |
вектор δc , |
|
ортогональный к c0 , из уравнения |
|
|
δc =δc′−(c†Sδc′)c . |
(43) |
|
0 |
0 |
|
В итоге мы получили лучшую аппроксимацию к собственному вектору. Процесс этот приближенный, ибо мы отбросили член второго порядка малости в (36). Так что, вообще, получим новый вектор c = c0 +δc , мы ренормируем этот
вектор и используем его как новый пробный вектор в этой итерационной процедуре. Уже отмечалось, что для сходимости требуется очень мало подобных итераций. Подчеркнем, что описанного процесса триангуляции важно, чтобы искомый собственный вектор имел ненулевую первую компоненту. Это ограничение практически не создает никаких дополнительных трудностей.
Полученные таким образом собственные векторы включаются в обычный итерационный процесс самосогласования, т. е. собственные векторы, полученные из решения уравнений (25) и (26), сравниваются с теми, которые использовались перед этим для построения фокианов (20) и (21). Процесс самосогласования в наших расчетах заканчивался тогда, когда компоненты каждого из вновь полученных векторов не отличались от компонентов соответствующего предыдущего вектора более, чем на 10–4. Опыт расчетов показал, что число итерационных циклов, ведущих от произвольных начальных векторов к самосогласованным, колеблется в пределах 7 – 10 циклов. Особенностью нашей атомной программы является то, что для всех интегралов были получены и запрограммированы конкретные формулы, в которые входят константы и показатели экспонент базисных функций. Такие формулы были получены не только для элементов матриц S и H , но и для элементов суперматриц P и Q . Суперматрицы на хранятся в памяти компьютера, а каждая их строка сворачивается с соответствующей матрицей плотности, так что фактически сразу по поределенным формулам строятся матрицы P и Q . Запрограммированы были также конкретные варианты построения матрицы Q , необходимой для данного состояния и конфигурации системы. Подобная специализация программы привела к ее большой эффективности в смысле скорости счета.
276

Описанную выше программу для расчета атомов с конфигурацией 1s2 2s2 2 pn в базисе гауссовых функций на языке АЛГОЛ можно найти в [39]. Программа может быть легко расширена для расчета более сложных атомов. Особенно просто это сделать, если открытая оболочка по симметрии не совпадает с закрытыми оболочками. В общем же случае потребуются еще дополнительные вычисления при построении матриц фокианов.
4.3.Систематический способ получения гауссовых базисных функций для атомных и молекулярных расчетов
Атомная программа, описанная в предыдущем разделе, использовалась для расчета основного состояния атомов B, C, N, O, F на примере которых изучалось как конкретно должны выбираться гауссовы базисные функции [38]. Корректность работы программы была проверена расчетом атома С в базисе 10s6p, взятом из работы Хузинаги [28]. Также проводился расчет для проверки возможности работы с округленными значениями показателей экспонент базисных функций: значения показателей экспонент, приведенные в [28] с 6-ю значащими цифрами, округлялись до 3 – 4 значащих цифр. Результаты этого и контрольного расчета приведены в табл. 5.
Таблица 5 Контрольный расчет основного состояния атома С (базис I) и влияние округления значений показателей экспонент базисных функций (базис II)
Показатели экспонент |
|
|
Собственные векторы |
|
|
|||||||
Базис I [28] |
Базис II |
|
1s |
|
2s |
|
2p |
|||||
(s) |
(p) |
(s) |
(p) |
Базис I |
|
Базис II |
Базис I |
|
Базис II |
Базис I |
|
Базис II |
9.40900 |
0.24805 |
9.41 |
0.248 |
0.42695 |
|
0.42695 |
–0.12134 |
|
–0.12134 |
0.43276 |
|
0.43315 |
84.5419 |
0.65771 |
84.5 |
0.658 |
0.07736 |
|
0.07736 |
–0.01701 |
|
–0.01701 |
0.35869 |
|
0.35859 |
307.539 |
1.78730 |
308 |
1.79 |
0.01934 |
|
0.01934 |
–0.00418 |
|
–0.00418 |
0.18262 |
|
0.18255 |
1397.56 |
5.77636 |
1400 |
5.78 |
0.00358 |
|
0.00358 |
–0.00076 |
|
–0.00076 |
0.05479 |
|
0.05481 |
3.50002 |
25.3655 |
3.5 |
25.4 |
0.35790 |
|
0.35790 |
–0.17554 |
|
–0.17554 |
0.00875 |
|
0.00875 |
1.06803 |
0.091064 |
1.07 |
0.0911 |
0.04877 |
|
0.04876 |
0.08502 |
|
0.08506 |
0.20351 |
|
0.20328 |
0.40017 |
|
0.4 |
|
–0.00756 |
|
–0.00756 |
0.60695 |
|
0.60739 |
|
|
|
26.9117 |
|
26.9 |
|
0.22679 |
|
0.22678 |
–0.05399 |
|
–0.05399 |
|
|
|
9470.52 |
|
9470 |
|
0.00045 |
|
0.00045 |
–0.00010 |
|
–0.00010 |
|
|
|
0.13512 |
|
0.135 |
|
0.00213 |
|
0.00213 |
0.43804 |
|
0.43759 |
|
|
|
Орбитальные энергии, ат. ед. |
–11.3252 |
|
–11.3252 |
–0.70554 |
|
–0.70560 |
–0.43304 |
|
–0.43291 |
|||
Полная энергия, ат. ед.: –37.687324 [28]; –37.687324 (Базис I); –37.687323 (Базис II)
Из табл. 5 видно, что округление показателей экспонент базисных функций не вносит существенных изменений в результаты, повышая значение полной энергии всего лишь на единицу шестого знака после запятой.
277

Поскольку критерием оптимальности базисного набора является значение энергии (§ 4.1), можно утверждать, что нет необходимости использовать более 3 – 4 значащих цифр в показателе экспонент гауссовых функций. Это упрощает пользование базисами гауссовых функций, хотя бы в чисто техническом отношении.
Перейдем теперь к вопросу о выборе базисных функций. Для краткости в дальнейшем под базисом будем подразумевать сам набор значений показателей экспонент и вместо термина «показатель экспоненты» будем говорить просто об экспонентах. В работе Хузинаги [28] приведены оптимальные базисы гауссовых функций размерности 9s5p и 10s6p для атомов от водорода до неона. Предложенный Хузинагой базис 10s6p достаточно гибок, чтобы получать хартри-фоковские решения для атомов, и широко используется в расчетах электронной структуры небольших молекул. Однако, часто мы хотим иметь скорее качественные, чем количественные результаты, а еще чаще интересующие нас молекулы слишком велики, так что, практически, точный расчет недоступен. В таких случаях желательно иметь более короткий атомный базис. Базис 7s3p для атомов второго периода представляет интерес для практического использования, поскольку он характеризуется оптимальной размерностью в смысле компромисса между точностью результатов и возможностью неэмпирического расчета достаточно больших молекул с разумными затратами времени счета [31, 40, 41]. Получить хороший базис 7s3p, механически выбрасывая некоторые экспоненты из более гибкого базиса, нельзя – результат будет неутешителен. Это утверждение подтверждается данными табл. 6.
Таблица 6 Неоптимальные расчеты энергии атомов (ат. ед.)
в базисе 7s3p
Атом Терм Базис 7s3p* Базис 7s3p [31, 40]
С |
3P |
–36.922099 |
–37.6192 |
N |
4S |
–53.312558 |
–54.2846 |
O |
3P |
–73.308438 |
–74.6326 |
F |
2P |
–97.447428 |
–99.1486 |
* Базис получен из базиса 10s Хузинаги [28] выбрасыванием экспонент с номерами 6, 8, 9 в том порядке как они приведены в его статье и из его базиса 5p выбрасыванием экспоненты с номером 4 и заменой 2-ой и 3-ей экспонент одной экспонентой.
Для получения базисов различной длины и точности желательно иметь определенные правила, позволяющие формировать базисные наборы для любого атома без предварительного использования компьютерной программы.
278

На возможность существования таких правил обратил внимание Ривс [33], но ни он сам, ни кто-либо другой не изучали эту возможность систематически. Лишь в [31] такая попытка была сделана, однако основная идея была искусственно усложнена, и как мы увидим ниже результаты этих авторов не оказались оптимальными.
Воспользовавшись этой идеей Ривса [33], покажем, как можно систематическим путем получать базисные наборы гауссовых функций для любого атома, исходя из разложений по гауссовым функциям собственных функций атома водорода [38].
При переходе от атома водорода к атому гелия в волновой функции основного состояния атома происходит изменение «эффективного заряда»:
e−r (H) e−1.6875r (He) . |
(44) |
Это изменение можно представить как масштабное преобразование
r 1.6875r . |
(45) |
Сравним, как изменяются соответствующие гауссовы функции. Оптимальное значение показателя экспоненты единственной гауссовой функции, описывающей основное состояние атома Н, равно 0.28294 (§ 4.1), атома Не – 0.76700 [33]. Переход
e−0.28294r2 (H) e−0.76700r2 (He)
соответствует преобразованию

 0.28294 r
0.28294 r 
 0.76700 r
0.76700 r
или
r 1.6462r , (46)
что незначительно отличается от преобразования (45). Использование этого факта и составляет суть предлагаемого подхода.
Правила Слэтера дают эффективное значение показателя экспоненты слэтеровской функции для данного атома по сравнению с атомом водорода. Например, чтобы получить волновые функции атома углерода нужно выполнить следующие замены в волновых функциях атома водорода:
ψ1s (H) e−r ψ1s (C) e−5.7r ,
ψ2s,2 p (H) e−12r ψ2s,2 p (C) e−3.225r.
Предположим теперь, что для атома водорода разложения собственных функций по гауссовым известны. Ясно, что для перехода от набора гауссовых
279
