Техническая механика / 4_Tekhnicheskaya_mekhanika_dlya_stroiteley

§2.6 ВЫЧИСЛЕНИЕ ГЕОМЕТРИЧЕСКИХ ХАРАКТЕРИСТИК СЕЧЕНИЙ СЛОЖНОЙ ФОРМЫ

Вслучае, когда поперечное сечение имеет сложную форму и его нельзя рассматривать как совокупность простейших геометрических фигур, внешнюю границу сечения аппроксимируют отрезками прямых, соединяющих точки, расположенные на этой границе. Нумерация точек на границе производится таким образом, чтобы возрастание номера осуществлялось при обходе сечения по часовой стрелке.

При таком представлении сложное сечение аппроксимируется совокупностью треугольных элементов, одна из вершин которых совпадает с началом координатной системыхOy, в которой рассматривается данное сечение. Площадь сечения и другие геометрические характеристики каждого такого треугольника выражаются через координаты соответствующих точек контура сечения i, j, образующих треугольный элемент Oij по следующим формулам:

-площадь сечения

- центробежный момент инерции относительно осей х и y

Суммируя выражения, вычисленные по этим формулам для всех элементов, получаем приближенные значения геометрических характеристик всего сложного сечения:

41

Отметим, что погрешность результатов вычислений тем меньше, чем точнее представление границы сечения узловыми точками контура, которых должно быть достаточно много. Далее определяем положение центра тяжести сечения по формулам

хc , yc относительно исходной системы координат хOy. Описанный алгоритм расчета может быть с легкостью реализован

на персональных ЭВМ.

ПРИМЕР 2.4

Исходные данные задачи.

Для заданного сечения сложной формы (рис. 2.15), требуется:

1)определить положения центра тяжести сечения;

2)найти положение главных центральных осей сечения;

3)вычислить главные центральные моменты инерции.

Решение задачи.

Рассмотрим поперечное сечение сложной формы, кусочнолинейная аппроксимация которого представлена на рисунке 2.15 в виде замкнутого многоугольника, построенного по 13 контурным точкам.

Численная реализация алгоритма вычисления геометрических характеристик сложных сечений по ранее приведенным формуламвыполнена в системе электронных таблицEXСEL. Предварительно определяем координаты контурных точек сечения (см. рис. 2.15).

42

В системе электронных таблиц для хранения и обработки данных используются ячейки, каждая из которых обозначается номером столбца (буквенные обозначения) и номером строки(цифровые обозначения). В первые три столбца таблицы(А-С) записываем исходные данные рассматриваемой задачи. Используя встроенные математические формулы EXСEL, составляем выражения для вычисления тех или иных геометрических характеристик в соответствии с известными формулами и проводим обработку содержимого заполненных ячеек электронной таблицы (рис. 2.16).

Более подробное описание вычислений в электронных таблицах EXСEL можно найти в его встроенной справочной системе. Результаты вычисления геометрических характеристик сечения сложной формы представлены на рисунке 2.16.

43

8.Какие моменты инерции всегда положительны?

9.Относительно каких осей центробежный момент инерции сечения равен нулю?

10.Чему равны осевые моменты инерции прямоугольника и треугольника относительно центральных осей, параллельных их основанию?

11.Чему равен осевой момент инерции круга относительно его -цен тральных осей?

12.Запишите зависимости для осевых и центробежного моментов инерции при параллельном переносе координатных осей.

13.Приведите формулы для осевых и центробежного моментов инерции при повороте координатных осей.

14.Как изменяется центробежный момент инерции при повороте координатных осей на 90°?

15.Относительно каких центральных осей осевые моменты инерции имеют наибольшее и наименьшее значения?

16.Как определить положение главных осей инерции?

17.Что такое радиусы инерции? Что такое главные радиусы инерции?

18.Что такое эллипс инерции?

19.Перечислите известные Вам геометрические характеристики плоского сечения бруса.

20.Какой осевой момент инерции круга больше: относительно центральной оси или относительно оси, параллельной центральной и касательной к кругу?

45

§3.2 ДЕФОРМАЦИИ ПРИ РАСТЯЖЕНИИ И СЖАТИИ. ПОНЯТИЕ

ОКОЭФФИЦИЕНТЕ ПУАССОНА. ЗАКОН ГУКА

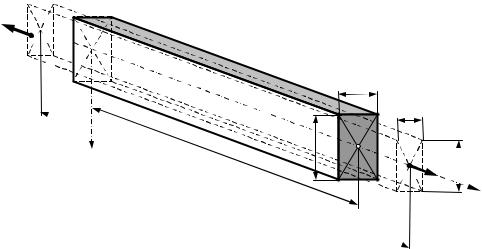
Рассмотрим деформации, возникающие при растяжении или сжатии призматических стержней. При растяжении длина стержня увеличивается, а поперечные его размеры сокращаются(рис. 3.2). При сжатии, наоборот, длина стержня уменьшается, а его поперечные размеры увеличиваются. При действии продольных сил первоначальная длина стержня l увеличивается на величину Dl . Удлинение стержня Dl на-

зывается абсолютной продольной деформацией, которая измеряется в единицах длины. Отношение первоначальной длины стержня l к вели-

чине Dl называется относительной продольной деформацией:

z

Рисунок 3.2

Высота и ширина поперечного сечения стержня уменьшаются на Dh и Db соответственно. Эти величины называются абсолютными поперечными деформациями. Отношение абсолютной поперечной - де формации к первоначальному размеру поперечного сечения стержня называется относительной поперечной деформацией:

ваются также линейными деформациями и являются безразмерными величинами. Для всех изотропных материалов eх = e у .

Абсолютное значение отношения относительной поперечной деформации к относительной продольной деформации в области упругих деформаций называется коэффициентом Пуассона:

48