Техническая механика / 4_Tekhnicheskaya_mekhanika_dlya_stroiteley

лельной оси х, второй индекс обозначает, что вектор касательного напряжения параллелен оси у.

Далее будем использовать следующее правило знаков для напряжений: нормальное напряжение s будем считать положительным, если оно направлено от грани элементарного объема. Знак касательных напряжений t связан с направлением координатных осей. Если внешняя нормаль к данной площадке совпадает с направлением какой-либо координатной оси, то на этой площадке напряжение будет положительным если его направление совпадает с другой осью. Если же внешняя нормаль противоположна направлению координатной оси, то направление t положительно если оно противоположно другой координатной оси. Это правило называют правилом внешней нормали.

Напряжения s y , s х , t yх и t ху при анализе плоского напряженно-

го состояния считаются заданными и поэтому их называютисходными напряжениями. Поворачивая элементарный параллелепипед в плоскости хOy можно получить такую его ориентацию, что все грани элементарного объема будут свободны от касательных напряжений. Нормальные напряжения, действующие по этим площадкам, будем называть главными напряжениями и обозначать s1 и s3 соответственно.

Приравнивая нулю сумму моментов всех сил, действующих по граням элементарного объема, относительно оси х получим следующее равенство:

Соотношение (4.1) называется законом парности касательных напряжений: на двух взаимно перпендикулярных площадках составляющие касательного напряжения, нормальные к линии пересечения площадок, равны по величине, а по направлению таковы, что стремятся повернуть элемент в противоположные стороны.

§ 4.2.1. НАПРЯЖЕНИЯ НА НАКЛОННЫХ ПЛОЩАДКАХ

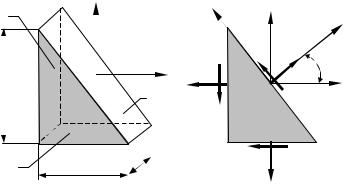
Далее будем рассматривать только одно семейство наклонных площадок - площадки, перпендикулярные ненагруженным граням элементарного параллелепипеда. Разрежем элементарный объем, изображенный на рисунке4.4, наклонным сечением, перпендикулярным плоскости хОу, выделив из него треугольную призму. Положение наклонной площадки и связанных с нею осейz' и у' будем определять углом a . Угол поворота осей считаем положительным, если поворот совершается против часовой стрелки. Из рисунка 4.3 следует, что dAх = dAcosa и dAy = dAsin a .

100

противоположные знаки. Подставляя выражения (4.8) и (4.10) в формулу (4.9), находим два корня квадратного уравнения

В этой формуле знак плюс соответствует максимальному главному напряжению s1 , а минус - минимальному напряжениюs 3 .

Напряжения, действующие по двум взаимно перпендикулярным площадкам, можно записать в виде матрицы второго порядка(4.12). Эта матрица называется тензором напряжений, а ее элементы явля-

ются компонентами тензора напряжений. Понятие тензора является более общим, чем понятие вектора. Тензоры часто используют в мате-

103

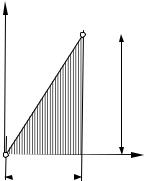
При условии, что площади граней элемента равны единице, нормаль-

Подставим в уравнение (4.17) обобщенный закон Гука (4.13), который запишем относительно главных напряжений и деформаций. Для этого необходимо заменить индексы х, у и z на 1, 2, 3 соответственно. Окончательно получаем следующее выражение удельной потенциальной энергии U для плоского напряженного состояния:

§ 4.7 КРУГИ МОРА ПРИ ПЛОСКОМ НАПРЯЖЕННОМ СОСТОЯНИИ

Зависимости напряжений sa и ta от угла наклона площадки a имеют простую геометрическую интерпретацию в виде круга Мора. За-

Введем следующие обозначения:

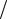a = (s1 + s 3 )2 и R = (s1 - s3 )2 ,

тогда

107

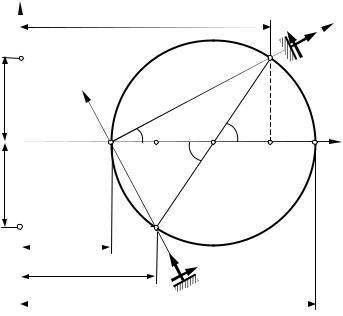
В координатах s -t равенства (4.19) представляют уравнение окружности радиуса R в параметрической форме, которая называется кру-

гом Мора для случая плоского напряженного напряжения, или кругом напряжений.

Рассмотрим прямую задачу, когда величины s1 и s 3 являются заданными и требуется определить величину и направление напряжений

имеем две точки В и А. На отрезке АВ, как на диаметре строим круг. Точку А в дальнейшем будем называть полюсом круга Мора. Используя точку А как вершину, откладываем заданный угол a от оси s (положительное направление угла – против часовой стрелки). Полученный луч пересекает окружность в точке K. Луч АK совпадает с направлением внешней нормали n , проведенной к наклонной площадке, где действуют напряжения sa и ta . Величина этих напряжений соответствует координатам точкиK в

координатах s -t . Соединяя точку K с центром круга О и продолжая полученную прямую до пересечения с окружностью, получаем точку K′. Координаты точки K′ соответствуют напряжениям sa +90o

Положение прямой АK′ совпадает с направлением внешней нормали к площадке a + 90o .

Теперь решим обратную задачу, когда заданы величины sa > 0 , ta > 0 , sa +90o < 0 , ta +90o < 0 и требуется установить положение главных

108

§ 4.8 КРИТЕРИИ ПРОЧНОСТИ И ПЛАСТИЧНОСТИ

Важнейшей задачей расчета элементов инженерных конструкций является оценка их прочности по известному напряженному состоянию. Наиболее просто такая задача решается для одноосного напряженного состояния, для которого значения предельных напряжений легко установить экспериментальным путем. Под предельными напряжениями понимают напряжения, соответствующие началу разрушения (для хрупких материалов) или появление значительных остаточных деформаций (для пластичных материалов).

Если материал находится в условиях плоского или объемного напряженного состояния, то экспериментальное определение предельных величин главных напряжений достаточно затруднено из-за сложности реализации подобных испытаний. Поэтому для решения подобной задачи необходимо разработать некоторый аналитический

критерий прочности.

109