
|
Решение задачи. |
|
|
|
|
|
|
|
|
|
|
|
Определяем величину опорных реакций заданной рамы. |
|
|
|
|
При решении подобных задач наибольшие трудности возникают |
при определении опорных реакций. Для каждой шарнирно неподвиж- |
|
|
|
М=20кНм |
|
ной |
опоры |
необходимо |
соста- |
|
|
|
|
вить и совместно решить два |
4 м |
q=8 |
4 |
С |
5 |
4 м |
уравнения |
статики: |
суммы |
мо- |
3 |
|
6 |
ментов |
относительно |
противо- |
|
2 |
|
|
|
В |
положной опоры и относительно |
|
1 |
|
HB |
RB |
врезного |
|
шарнира |
|
левых |
или |
4 м |
|
|
|
|
|
|
|
правых |
сил |
должны |
|
равняться |
F=10кН А |
|
|
|
|
|
|
HA |
|
|
|
нулю. |
Определяем |
опорные |
-ре |
|
RA |
|
|
|
|
|
3 м |
5 м |
|
5 м |
|
акции в шарнирно неподвижной |
|
|
Рисунок 6.30 |
|
опоре B. Составляем уравнение |
|
|
|
суммы моментов левых сил от- |
носительно врезного шарнира и записываем выражение для горизон- |
тальной опорной реакции H B : |
|
|
|
|
|
|
|
|
|
|
|
åтСлев = 0 ; |
|
H B × 4 - M + RB × 5 = 0 ; |
H B |
= (20 - RB ×5) |
4 . |
|
|
|
Далее записываем уравнение суммы моментов всех сил, прило- |
женных к раме, относительно шарнирно неподвижной опоры A: |
|
|
åтA = 0 ; H B × 4 - F ×3 - q × 4 ×6 + M - RB ×10 = 0 .
Вэто уравнение подставляем ранее полученное выражение для горизонтальной опорной реакцииH B и находим величину
вертикальной опорной реакции R B . Тогда
20 -R B ×5 -10 ×3 - 8 × 4 × 6 + 20 -R B ×10 = 0 ; -R B ×15 -182 = 0 ;
R B = -182 15 = -12,13 кН.
15 = -12,13 кН.
Отсюда
H B = (20 - (-12,133)×5) 4 = 20,17 кН.
4 = 20,17 кН.
Аналогичным образом определяем вертикальную и горизонтальную опорные реакции в шарнирно неподвижной опоре A.
åтСпр = 0 ; H А ×8 - RА ×5 - F ×8 + q × 42  2 = 0 ; RА = (H А ×8 - F ×8 + q × 42
2 = 0 ; RА = (H А ×8 - F ×8 + q × 42  2)
2) 5 .
5 .
åтB = 0 ; RA ×10 - H A × 4 + F ×13 + q × 42  2 - M = 0 ;
2 - M = 0 ;
H A ×16 + F ×13 - F ×16 + 2 × q × 42 2 + q × 42 2 - M - H A × 4 = 0 ;
12,13
12,13
|
|
- |
+ |
20,17 |
20,17 |
|
- |
12,13 |
|
|
22,13 |
|
12,13 |
+ Эп. Nz
22,13
--
12,13
12,13
+
10,0
10,0
+
+Эп. Qy
11,83
H A = (F ×3 - 3 × q × 42  2 + M )
2 + M )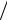 12 =
12 =
= (10 ×3 - 3 ×8 × 42  2 + 20)
2 + 20) 12 = -11,83кН; RА = (-11,833 ×8 -10 ×8 + 8 × 42
12 = -11,83кН; RА = (-11,833 ×8 -10 ×8 + 8 × 42 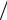 2)
2) 5 =
5 =
= -22,13 кН.
Для проверки найденных значений опорных реакций рамы составляем уравнения суммы проекций всех сил на горизонтальную и вертикальную оси:
åх = 0 ;
q × 4 - H B + H A = 0 ;
60,67 |
8 × 4 -11,83 - 20,17 = 32,0 - 32,0 = 0 ; |
60,67 |
|
|
|
80,67 å y = 0 ; |
|
|
|
|
|
|
|
60,67 |
|
|
|
|
|
F - RB + RA = 0 ; |
|
|
|
|
86,08 |
|
|
|
|
|
|
|
|
10 +12,13 - 22,13 = 22,13 - 22,13 = 0 . |
|
|
47,33 |
|
|
|
|
77,33 |
|
|
|
30,0 |
|
|
|
|
|
Следовательно, опорные реакции ра- |
|
|
Эп. Mx |
|
|
|
|
|
|
|
|
|
|
|
мы найдены верно. |
|
|
|
Рисунок 6.31 |
Рассмотрим первый грузовой |
|
|
|
|
|
|
участок 0 £ z1 £ 4 м. |
|
|
|
|
|
|
|
|
å z = 0 ; RА + N z = 0 ; N z |
= -RА = -22,13 кН; |
|
å y = 0 ; Qy |
+ H A = 0 ; Qy |
= -H A =11,83 кН; |
|
åm = 0 ; M x + H A z1 = 0 ; M x = -H A z1 . |
при z1 |
= 0 м; |
M x = 0 кНм; |
при z1 |
= 4 м; |
M x = 47,33 |
кНм. |
Второй грузовой участок 0 £ z2 £ 3 м.
åz = 0 ; N z = 0 кН;
åy = 0 ; Qy - F = 0 ; Qy = F =10,0 кН;
åm = 0 ; M x - Fz2 = 0 ; M x = Fz2 .
при z2 = 0 м; M x = 0 кНм;
при z2 |
= 3 м; |
M x = 30,0 кНм. |
Третий грузовой участок 4 £ z3 £ 8 м. |
å z = 0 ; |
|
RА + N z + F = 0 ; |
|
|
|
N z = -RА - F = -12,13 кН; |
å y = 0 ; |
|
Qy + H A + q(z3 - 4)= 0 ; |
|
|
|
Qy = -H A - q(z3 - 4); |
åm = 0 ; |
M x + H A z3 - 3F + q(z3 - 4)2 2 = 0 ; |
|
|
M x = -H A z3 + 3F - q(z3 - 4)2 2 . |
при z3 |
= 4 м; |
Qy |
=11,83кН; |
|
|
M x |
= 77,33 кНм; |
при z3 |
= 8м; |
Qy |
= -20,17 кН; |
|
|
M x |
= 60,67 кНм. |
при z3 |
= 5,479 м; |
Qy |
= 0 кН; |
|
|
M x |
= 86,08 кНм. |
Четвертый грузовой участок 0 £ z4 £ 5 м
|
|
|
|
|
|
|
|
å z = 0 ; |
Н А + N z |
+ 4q = 0 ; N z |
= -Н А - 4q = -20,17 кН; |
å y = 0 ; |
- RА - F + Qy = 0 ; Qy |
= RА + F = -12,13 кН; |
åm = 0 ; |
M x - RА z3 + 8H A - F (z3 + 3)+ q ×32 2 = 0 ; |
|
|
M x = RА z3 - 8H A + F (z3 + 3)- q ×32 2 = 0 ; |
при z4 |
= 0 м; |
M x |
= 60,67 кНм; |
|
|
при z4 |
= 5 м; |
M x |
= 0 кНм. |
|
|
|
Шестой грузовой участок 0 £ z6 |
£ 4 м |
å z = 0 ; |
- RB + N z |
= 0 ; |
N z |
= RB = -12,13 кН; |
å y = 0 ; |
- H B + Qy |
= 0 ; |
Qy |
= H B = 20,17 кН; |
åm = 0 ; |
M x - H B z6 = 0 ; M x = H B z6 ; |
при z6 |
= 0 м; |
M x |
= 0 кНм; |
|
|
|
при z6 |
= 4 м; |
M x |
= 80,67 кНм. |
|
Пятый грузовой участок 0 £ z5 £ 5 м |
å z = 0 ; |
H B + N z = 0 ; N z = -H B |
= -20,17 кН; |
å y = 0 ; |
- RB + Qy = 0 ; Qy = RB |
= -12,13 кН; |
åm = 0 ; |
M x + RB z5 + 4H B - M = 0 ; M x = -RB z5 - 4H B + M ; |
при z5 |
= 0 м; |
M x |
= -60,67 кНм; |
|
при z5 |
= 5 м; |
M x |
= 0 кНм. |
|
По полученным значениям строим эпюры внутренних силовых факторов в заданной раме(рис. 6.31). Проверку равновесия узлов студентам предлагается выполнить самостоятельно.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ К ГЛАВЕ 6
1.Какие виды внешних нагрузок действуют на брус?
2.Что называется эпюрой внутренних силовых факторов?
3.Для чего необходимо выполнять построение эпюр внутренних -си ловых факторов?
4.Что называется грузовым участком?
5.Каков порядок построения эпюр внутренних усилий с помощью метода сечений?
6.Сформулировать правила знаков для внутренних силовых факторов и пояснить их рисунками.
7.Какие внутренние усилия возникают в балке при плоском поперечном изгибе?
8.Запишите дифференциальные уравнения равновесия произвольно нагруженного элемента бруса.
9.Какая интегральная зависимость существует между изгибающими моментами и поперечными силами в пределах грузового участка?
10.Перечислите правила контроля эпюр поперечных сил.
11.Что возникает на эпюре изгибающих моментов в сечении, где поперечная сила пересекает нулевую линию?
12.Перечислите правила контроля эпюр изгибающих моментов.
13.Как можно построить эпюры внутренних усилий без составления уравнений равновесия для отсеченной части балки?
14.Какими будут опорные реакции, эпюры поперечных сил и изгибающих моментов для симметрично нагруженной симметричной балки?
15.Какими окажутся опорные реакции, эпюры поперечных сил и изгибающих моментов для кососимметрично нагруженной, но симметрично устроенной балки?
16.Как изменяются эпюры Qy и M x на участке, загруженном распре-
деленной нагрузкой, изменяющейся по линейному закону?
17.Что называется рамой?
18.Какое условие должно выполняться в узлах плоской рамы?
19.Как изменяются эпюры продольных и поперечных сил в наклонном стержне, загруженном вертикальной равномерно распределенной нагрузкой?
20.Какое дополнительное уравнение равновесия можно записать для рамы, имеющей врезной шарнир?
лярных линий (рис. 7.2). Приложим к торцам бруса равные моменты Mх. Таким образом балка работает в условиях чистого изгиба. После ее деформации линии параллельные оси станут дугами окружностей, а линии перпендикулярные оси станут отрезками радиусов(рис. 7.2). Рассматривая картину деформации можно сформулировать несколько гипотез:
1.Выполняется гипотеза плоских сечений(сечения плоские до деформации остаются плоскими после деформации).
2.Длина отрезка ef в направлении перпендикулярном оси в процессе деформации не изменяется, следовательно, можно предположить, что продольные волокна не давят друг на друга.
3.Длина отрезка ab сократилась, а отрезка cd увеличилась. Следовательно, в верхней части балки волокна сжимаются, а в нижней растягиваются. Следовательно, имеются волокна, которые не сжимаются и не растягиваются. Совокупность таких волокон в поперечном сечении бруса составляютнейтраль-
ный слой.
 Центр кривизны
Центр кривизны
|
r |
dj |
|
|
|
|
smin |
|
|
|
|
|
|
|
Mx |
|
|
|
Mx |
|
|
x |
|
|
|
|
|
|
|
dNz y |
|
Нейтральный слой |
z dNz |
х |
K |
С |
|
|
|
|
2′ |
|
y |
1′ |
1 |
|
2 |
|
|
dA |
ds+D ds |
|
|
|
|
|
ds |
|
|
|
|
|
|
|
|
|
|
|
y |
|
dz |
|
|
|
|
y |
|
|
|
|
|
|
Рисунок 7.3
Рассмотрим два нормальных сечения балки, находящихся на бесконечно малом расстоянии dz1 друг от друга (рис. 7.3). Первоначально прямолинейное волокно 1-2 после деформации станет дугой окружности 1′-2′ радиуса r + у. Величина r равна радиусу кривизны нейтрального слоя. Учитывая, что продольные волокна не давят друг на друга, можно считать, что волокно 1′-2′ работает только на растяжение. Если материал балки работает в линейно-упругой области, то

Определим относительную деформацию ez рассматриваемого во-
локна. Длину волокна 1-2 до деформации обозначим как ds , а после деформации – ds + Dds . Тогда
ez = (ds + Dds)- ds = Dds . ds ds
Но с другой стороны, как следует из рисунка 7.3, длину этого волокна до деформации можно записать как
ds = r dj ,
а после деформации его длина соответственно равна ds + Dds = (r + у) dj .
Таким образом, окончательно получаем |
|
|
|
|
ez = |
Dds |
= (r + у)dj - r dj |
= |
у |
. |
(7.2) |
|
|
|
ds |
|
r dj |
|
r |
|
Учитывая, что при y > 0 |
волокна балки растягиваются, |
подстав- |
ляя выражение (7.2) в уравнение (7.1) имеем |
|
|
|
|
|
|
s z |
= |
E |
y. |
|
|
|
(7.3) |
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
Следовательно, нормальные напряжения s |
изменяются по высоте се- |
чения по линейному закону. |
|
|
|
|
|
|
|
При изгибе балки в волокне 1-2 возникает элементарная растягивающая сила dN . В поперечном сечении балки рассматриваемое -во
локно соответствует точке K. Выделим в ее окрестности |
бесконечно |
малую площадку dA . Тогда величина элементарной силы dN равна |
dN z = s z dA . |
(7.4) |
В соответствии с определением чистого изгиба в поперечном сечении балки продольная сила отсутствует. Тогда, интегрируя выраже-
ние (7.4) по площади А, получаем |
|
N z = òòs z dA = 0 . |
(7.5) |
|
|
А |
|
Подставляя уравнение (7.3) в (7.5), имеем |
|
|
E |
òò y dА = 0 . |
(7.6) |
|
r |
|
|
А |
|

Отношение Е / r не равно нулю, отсюда òòy dА = 0 . Но этот ин-
А
теграл представляет собой статический момент S x площади поперечного сечения балки относительно нейтральной оси Ох. Известно, что если S x = 0 , то ось Ох проходит через центр тяжести поперечного сечения
балки. Следовательно, при изгибе нейтральный слой проходит через центр тяжести и совпадает с одной из главных центральных осей, т.к. мы рассматриваем балки с симметричным сечением.
В соответствии с выражением(1.9) изгибающий момент можно определить следующим образом
M x = òòs z ydA .
A
Подставляя в это уравнение выражение (7.3), получаем
|
|
|
|
|
|
|
|
|
|
|
|
M x = òò |
Е |
y2 dA = |
Е |
òò y2 dA = |
ЕJ |
|
|
|
|
x |
. |
(7.7) |
r |
r |
r |
A |
|
|
|
|
|
A |
|
|
|
здесь J x - момент инерции сечения бруса относительно оси Ох. |
|
Тогда, кривизна изогнутой оси балки будет равна |
|
|
|
|
1 |
= |
M x |
. |
|
|
(7.8) |
|
|
|
|
|
|
|
|
|
|
r |
EJ x |
|
|
|
Подставляя выражение (7.8) в уравнение (7.3), получаем формулу для определения нормальных напряжений при чистом изгибе
s z = M x y. (7.9)
J x
Как следует из полученного выражения, экстремальные нормальные напряжения возникают в точках поперечного сечения наиболее удаленных от нейтральной оси Ох
smax |
= |
M x |
ymax |
= |
M x |
, |
(7.10) |
|
|
|
|
J x |
|
Wx |
|
где Wx = J x / ymax - момент сопротивления поперечного сечения балки. Учитывая, что волокна балки испытывают деформации растяже-
ния или сжатия, можно записать условие прочности
smax |
= |
M x |
£ R, |
(7.11) |
|
|
|
Wx |
|
где R - расчетное сопротивление для данного материала.

§7.2 КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ ПРИ ПОПЕРЕЧНОМ ИЗГИБЕ
При поперечном изгибе в произвольной точке сечения балки K возникают не только нормальные напряжения s z , но и касательные напряжения t zy (рис. 7.1). В соответствии с законом парности касатель-
ных напряжений в продольных сечениях балки возникают касательные
|
|
напряжения t уz . Эти напряжения вызывают |
|
|
сдвиги отдельных волокон балки относи- |
|
|
тельно друг друга. Вследствие сдвигов ги- |
|
K |
потеза плоских сечений нарушается и пло- |
|
n |
ские до деформации сечения получают не- |
|
|
которое искривление (рис. 7.4). |
|
tyz |
Экспериментальные |
и |
теоретические |
|
sz |
исследования показали, что если высота по- |
|
n |
перечного сечения h значительно меньше |
|
tzy |
|
длины балки l |
( h / l <<1), |
то |
эти искривле- |
|
K |
ния заметным |
образом |
не |
сказываются на |
Рисунок 7.4 |
работе балки на изгиб. В таком случае гипо- |
|
теза плоских сечений считается условно справедливой. Следовательно, для расчета нормальных напряжений sz при поперечном изгибе можно применять формулу (7.9), полученную для случая чистого изгиба.
Выделим бесконечно малый участок балки длинойdz2 (рис. 7.1), где поперечная сила Qy = const . Разрежем элемент дополнительным
сечением, параллельным плоскости zOx (рис. 7.5). Рассмотрим равновесие его нижней части. К левому сечению элемента приложен изгибающий момент M x , а к правому сечению- момент M x + d M x . Следовательно, нормальные напряжения в правом сечении получают приращение ds . Величина этого приращения может быть определена по фор-
муле (7.9)
ds = dM x y1 , J x
где y1 - координата произвольной точки K , принадлежащей нижней отсеченной части элемента.
Очевидно, что равнодействующая нормальных напряжений в правом сечении больше, чем в левом сечении. Приращение растягивающей силы равно
|
|
|
|
|
|
|
|
|
dN z = òòds × dA = òò |
dM |
x |
y1dA = |
dM |
x |
òòy1dA . |
(7.12) |
J |
|
J |
|
Acut |
Acut x |
|
|
x |
|
Acut |
|










 15
15  4
4 




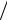
 2
2  12
12 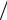 2
2 5
5  Центр кривизны
Центр кривизны