
17.Как с помощью круга Мора найти напряжения на двух взаимно перпендикулярных произвольных площадках по заданным главным напряжениям?
18.Что принято за критерий прочности в I гипотезе прочности?
19.Записать условия прочности поI гипотезе прочности. Что принято считать причиной разрушения материала в I гипотезе прочности?
20.Для каких материалов применима I гипотеза прочности?
21.Что принято за критерий прочности во II гипотезе прочности?
22.Что принято считать причиной разрушения материала во II гипотезе прочности?
23.Записать условия прочности поII гипотезе прочности. Для каких материалов применима II гипотеза прочности?
24.Что принято за критерий прочности в III гипотезе?
25.Записать условие прочности по III гипотезе прочности.
26.Что принято считать причиной разрушения материала вIII гипотезе прочности?
27.Для каких материалов применима III гипотеза прочности?
28.Как отличаются формулы для полной удельной энергии деформации и удельной энергии формоизменения?
29.Что принято за критерий прочности в IV гипотезе?
30.Записать условие прочности по IV гипотезе прочности.
31.Что принято считать причиной разрушения материалов в IV гипотезе прочности?
32.Для каких материалов применима IV гипотеза прочности?
33.Что принято за критерий прочности в гипотезе Мора?
34.Записать условие прочности по гипотезе Мора.
35.Для каких материалов применима гипотеза Мора?
120

ГЛАВА 5.
СДВИГ И КРУЧЕНИЕ
§ 5.1 ПОНЯТИЕ О ЧИСТОМ СДВИГЕ. АНАЛИЗ НАПРЯЖЕННОГО СОСТОЯНИЯ ПРИ ЧИСТОМ СДВИГЕ
При чистом сдвиге в сечениях бруса действуют только поперечные силы Qx или Qy . Если в окрестности некоторой точки, принадле-
жащей этому сечению, выделить прямоугольный элемент, то он будет испытывать только деформацию сдвига. Удлинения его сторон будут равны нулю. По граням такого элемента действуют только касательные напряжения t хy = t yх (рис. 5.1). Таким образом, чистый сдвиг это та-
кой вид плоского напряженного состояния, при котором на двух взаимно перпендикулярных площадках действуют только касательные напряжения. Эти площадки называют площадками чистого сдвига.
|
|
Принимая площадки чистого сдвига за исходные и полагая, что |
|||||||||||||
s х = s y |
= 0 и t хy |
= t , получим: |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
sa |
=t sin 2a , |
|
|
|
(5.1) |
||
|
|
|
|
|
|
|
|
ta |
=t cos 2a . |
|
|
|
(5.2) |
||
|
y |
′ |
y |
|
|
|
|
|
|
Найдем |
величину |
экстремальных |
|||
|
|
|
|
|
напряжений при сдвиге. Когда |
a = 45° |
|||||||||
|
|
tyх |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
имеет |
место |
максимальное |
нормальное |
||||
|
|
|
ta |
|
|
|
х′ |
||||||||
|
sa+90° |
ta |
sa |
|
напряжение |
s1 |
=t , а при a = 135° - ми- |
||||||||
|
|
|
|
|
|
||||||||||
tхy |
|
|
|
|
|
a нимальное |
напряжение |
s 3 |
= -t . Экс- |
||||||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
х |
тремальные |
касательные |
напряжения по |
|||||
|
|
|
|
|
|
tхy |
формуле (5.2) равны t max =t . |
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||||
|
sa ta |
|
|
|
|
|
|
||||||||
|
sa+90° |
|
|
|
|
Итак, |
при чистом |
сдвиге |
главные |
||||||
|
|
|
ta |
|
|
напряжения равны между собой и чис- |
|||||||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
tyх |
|
|
|
ленно |
равны |
экстремальным |
касатель- |
|||||
|
|
|
Рисунок 5.1 |
|
|
ным |
напряжениям. Главные |
площадки |
|||||||
|
|
|
|
|
|
|
|
составляют с площадками чистого сдвига |
|||||||
угол 45°. Чистый сдвиг представляет собой единственный вид плоского напряженного состояния, при котором отсутствует изменение объема материала, а любой выделенный элемент при чистом сдвиге изменяет только форму.
§5.2. ЗАКОН ГУКА ПРИ СДВИГЕ. ЗАВИСИМОСТЬ МЕЖДУ МОДУЛЯМИ УПРУГОСТИИ ПЕРВОГО И ВТОРОГО РОДА
Рассмотрим деформацию элемента, ограниченного площадками чистого сдвига (рис. 5.2). Величину d называют абсолютным сдвигом,
121

а отношение d / а » g - относительным сдвигом, или углом сдвига.
Экспериментально установлено, что в определенных пределах деформация сдвига происходит упруго, а величина ее пропорциональна касательным напряжениям t :
g = t G ,
G ,
или |
|
t = Gg . |
(5.3) |
Это соотношение называют законом Гука при сдвиге. Коэффициент пропорциональности G между касательным напряжением и углом сдвига называют модулем упругости при сдвиге, или модулем упруго-
сти второго рода. Величина модуля G определяется экспериментально. Для каждого материала модуль сдвига G имеет свое значение. Так, для стали G » 0,8×105 МПа.
Типичный вид диаграммы деформации сдвига в осяхt - g для пластичной стали показан на рисунке5.2. Эта диаграмма аналогична диаграмме при растяжении. Напряжение t pr называется пределом про-
порциональности при сдвиге и является границей справедливости зако-
на Гука (5.3). Точка t у соответствует пределу текучести при сдвиге.
Так же как и при растяжении, при постоянном напряжении t =t у на-
блюдается значительный рост сдвигов(текучесть при сдвиге), сменяющийся затем стадией упрочнения.
а
d |
t |
|
d |
|
|
|
t |
|
|
|
g |
|
|
|
t |
|
|
t |
|
|
|
|
|
y |
|
|
|
pr |
t |
|
|
|
t |
|
|
|
t |
a |
|
|
а |
0 |
g |
|
|
|
|||
|
|
|
Рисунок 5.2
Тангенс угла наклона диаграммы на ее линейном участке относительно горизонтальной оси численно равен модулю сдвига материала
tga = tg = G .
Рассмотрим бесконечно малый элемент материала, находящийся в условиях чистого сдвига (рис. 5.3). Удлинение Ds диагонали АС с одной стороны является следствием деформации сдвига и, значит, при заданных напряжениях t зависит от модуля G. С другой стороны, диаго-
122

наль АС можно представить как волокно материала, растягиваемое на- |
||||||||||
|
|
|
|
|
|
пряжением s1 и сжимаемое в попереч- |
||||
|
d |
t |
|
d |
|
ном |
направлении |
напряжением s 3 . |
В |
|
B |
|
|
C |
C |
этом |
случае удлинение Ds зависит |
от |
|||
|
|
|
||||||||
|
s3=-t |
s1=t |
|
|
модуля упругости Е . Это позволяет |
|||||
|
|
|
|
|
Ds |
сделать вывод о том, что модули G и |
||||
аt |
g |
|
|
t |
Е зависят друг от друга. |
|
|
|||
|
s1=t s3=-t |
|
|
Удлинение диагонали АС вслед- |
||||||
|
|
ствие деформации сдвига равно |
|
|||||||
|
45° |
|
|
s |
|
|
||||
|
|
|
t |
|
|
|
|
2 ag . |
|
|
A |
|
а |
D |
|
|
Ds = d cos 45o = |
|
|||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
2 s |
2 |
|
|
|
|
|
|
|
|
a = s cos 45o = |
и g = t . |
|
|
|
Рисунок 5.3 |
|
|
|
2 |
G |
|
|||
|
|
|
Ds = t s . |
|
|
|||||
|
|
|
|
|
|
|
|
2G |
|
|
С другой стороны, применяя к волокну АС обобщенный закон Гука, |
||||||||||
можно записать |
|
|
|
|
|
|
|
|||
e1 = Ds = s1 - m s3 . s E E
Подставляя s1 =t и s 3 = -t , имеем
Ds = 1 + m st .
E
Приравнивая два выражения полученных для Ds , записываем искомое соотношение
|
E |
|
G = |
2(1 + m). |
(5.4) |
§ 5.3 ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ПРИ ЧИСТОМ СДВИГЕ
При деформации элемента, ограниченного площадками чистого сдвига, показанного на рисунок 5.4, работу совершает только касательная сила Т, приложенная к его верхней грани на перемещении d . При условии, что размер элемента, перпендикулярный чертежу равен единице, сдвигающая сила равна Т =tа ×1. Если материал работает в ли- нейно-упругой области, то величина сдвига d пропорциональна силе сдвига Т. Работа этой силы А и, следовательно, соответствующая ей потенциальная энергия сдвига U определяются как заштрихованная площадь под диаграммой сдвига (рис. 5.4). Тогда
A = U = 1 Td .
2
123

d |
|
|
Т=tа |
d |
|
Учитывая, |
что сила равна |
|||
|
|
|
|
|
|
Т |
|
Т =tа , а |
абсолютный |
|
|
|
|
|
|
|
|
|
|||
|
|
g |
|
|
|
|
сдвиг d = gа , получаем |
|||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||
а |
Т=tа |
Т=tа |
Т |
U= 1 tgа2 .
2
|
|
|
|
Объем элемента V = а2×1, |
||||||
|
|
|
|
поэтому |
удельная |
потен- |
||||
Т=tа |
0 |
|
||||||||
а |
d |
d циальная |
энергия |
сдвига |
||||||
|
|
|||||||||
|
|
|
|
равна |
|
|
|
|
||
|
Рисунок 5.4 |
|
и = |
U |
= |
1 |
tg . |
(5.5) |
||
|
|
|
|
|||||||
|
|
|
|
V |
|
|||||
|
|
|
|
|
2 |
|
|
|||
Применяя закон Гука при сдвиге (5.3), окончательно получаем |
|
и = 1 t 2 . |
(5.6) |
2G
§5.4 РАСЧЕТ ЗАКЛЕПОЧНЫХ И БОЛТОВЫХ СОЕДИНЕНИЙ
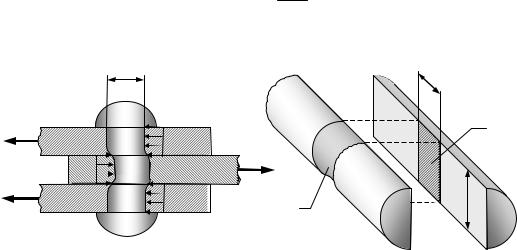
Рассмотрим работу одиночной заклепки, соединяющей три листа (рис. 5.5). Разрушение такого соединения может быть вызвано срезом заклепки по двум плоскостям m-n и m1-n1. Такая заклепка называется двухсрезной. Аналогичным образом работает и болтовое соединение. Все дальнейшие выкладки относятся как к заклепочным, так и к болтовым соединениям.
Определим предельную силу Fsmax , которую может выдержать одна двухсрезная заклепка. Будем считать, что заклепочное соединение теряет несущую способность, когда касательные напряжения по плоскостям сдвига становятся равными пределу текучести. В качестве расчетной прочностной характеристики принимаем расчетное сопротивление среза Rs , определяемое экспериментально. Предполагаем, что в предельном состоянии касательные напряжения равномерно распределены по плоскостям среза и равны Rs . Тогда
F max = пА R |
= п |
pd 2 |
R |
. |
|
|
|||||
s |
s s |
4 |
s |
|
|
|
|
|
|
||
где Аs - площадь среза заклепки; d - диаметр заклепки;
п - число плоскостей среза (для двухсрезной заклепки п = 2).
Если заклепочное соединение содержит несколько заклепок, то будем считать, что сила равномерно распределена между заклепками
124
Fsmax = пk pd 2 Rs .
4
где k - количество заклепок в заклепочном соединении.
d |
|
|
d |
F/2 |
|
|
|
m |
n |
F |
|
|
|
|
|
F/2 |
n1 |
|
|
m1 |
Фактическая |
d |
|
|
|
|
|
|
|
поверхность |
|
|
|
смятия |
|
Рисунок 5.5
(5.7)
Условная
площадь
смятия
Помимо среза при относительно тонких листах возможно нарушение соединения вследствие смятия, как листов, так и заклепки в месте их контакта. Действительное распределение напряжений по поверхности контакта достаточно сложное. Однако, приближенно можно считать, что они равномерно распределены по проекции поверхности контакта на диаметральную плоскость заклепки Acol = dd . Эта площадь называется условной площадью смятия (рис. 5.5). В общем случае, при наличии в соединении нескольких листов, обладающих разными толщинами di , суммарная площадь смятия равна
n |
|
Acolmin = d ådi . |
(5.8) |
i =1
n
где ådi - суммарная толщина сминаемых листов.
i =1
Экспериментально устанавливается величина расчетного сопротивления материала смятия Rcol . Тогда предельная сила, которую может воспринять заклепочное соединение из условия смятия равна
F |
£ Amin R . |
(5.9) |
col |
col col |
|
Очевидно, что в качестве расчетного усилия для заклепки принимается наименьшая из двух сил, найденных из условий смятия и среза.
§ 5.5 ОСНОВЫ РАСЧЕТА СВАРНЫХ СОЕДИНЕНИЙ НА СРЕЗ
Рассмотрим принцип расчета сварного соединения из двух листов с угловыми швами (рис. 5.6). Сварные соединения не создают местных
125

ослаблений элементов и являются менее трудоемки, чем другие виды соединений.
Разрушение сварных швов происходит от среза по площадкам, наклоненным под углом 45° относительно плоскости соединяемых листов. Расчетное поперечное сечение шва приближенно заменяется треугольником. Если обозначить высоту шва через h, то площадь среза для двух швов будет равна:
As = 2lhb ,
где b - коэффициент, зависящий от вида сварки(для ручной сварки b = 0,7 , для автоматической сварки b = 1,0 );
h - высота катета сварного шва.
F
h
h
l |
0,7 |
As
As
F
Сварной шов
Рисунок 5.6
Предполагается, что касательные напряжения по площади среза шва распределены равномерно. Тогда условие прочности имеет вид
t = |
F |
= |
F |
£ Rs , |
(5.10) |
|
2lhb |
||||
|
As |
|
|
||
где Rs - расчетное сопротивление материала сварного шва на срез;
l - расчетная длина одного шва, которая берется на 10 мм меньше фактической длины из-за возможного непровара шва.
Задавшись высотой шва h , по формуле (5.10) можно найти требуемую длину сварного шва.
§5.6 НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ ПРИ КРУЧЕНИИ СТЕРЖНЯ КРУГЛОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
Кручением называют такой случай деформации прямого бруса, при котором в его поперечных сечениях возникают только крутящие моменты M z . На кручение работают многие детали строительных машин и механизмов. Стержень, работающий на кручение, принято назы-
126

вать валом. Экспериментальные исследования показали, что характер деформаций при кручении в значительной степени зависит от формы поперечного сечения стержня.
Рассмотрим кручение вала с круглым или кольцевым сечением, которые наиболее часто используются в технике. При кручении вала происходит поворот одного поперечного сечения относительно другого на некоторый угол dj , который называется углом закручивания.
|
|
l |
|
|
|
dz |
|
|
|
|
|
|
|
|
|
|
|
||
|
z |
|
dz |
|
|
tmax |
|
|
|
|
|
|
|
|
|
tr |
|
||
|
|
|
|
Mz |
|
|
Mz |
||
|
|
d′ |
b′ |
|
|
|
|||
|
c′ |
|
|
d′ |
|
|
|||
|
|
j+dj j |
z |
|
dj |
|
|||
|
|
|
|
|
|
||||
|
|
j |
l |
|
|
k′ |
|
|
|
|
c |
b |
e |
gr |
r |
z |
|||
a |
d |
k |
|||||||
c |
r |
||||||||
|
|
|
Mz |
g |
d |
|
|
||
|
|
|
|
|
|
|
|
Рисунок 5.7
На боковой поверхности вала проведем образующую ab, которая после приложения крутящего момента займет новое положениеab'. В результате сечение, взятое на расстоянии z от заделки, повернется на угол j , а соседнее с ним сечение, проведенное на расстоянии dz - на угол j + dj (рис. 5.7).
Отдельно рассмотрим элемент вала длиной dz. Будем считать левое сечение неподвижным, тогда соседние сечения поворачиваются на угол dj . Образующая cd отклонится на малый угол g и займет новое положение cd'. Угол сдвига волокна, принадлежащего поверхности вала, определяется равенством
g = dd ¢ = rdj
cd dz
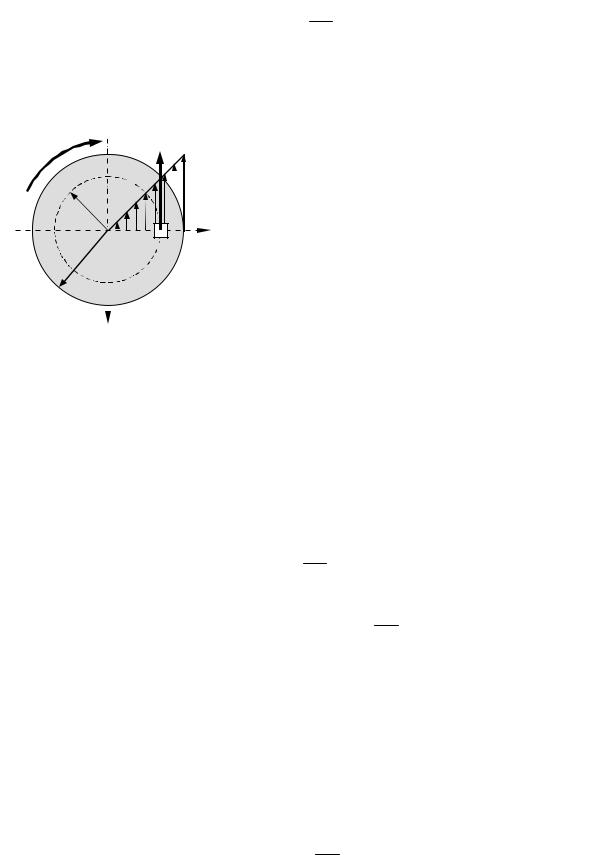
Для произвольного волокна, находящегося на расстоянии r от центра круга, имеем
g r= kk¢ = rdj . cd dz
На основании закона Гука при сдвиге(5.3) для двух указанных точек можно записать:
t = gG = G |
dj |
r , |
(5.11) |
|
dz
127
|
|
t r |
=g rG = G dj r . |
|
|
|
(5.12) |
|
|
|
|
dz |
|
|
|
|
|
Сопоставляя полученные формулы, можно сделать вывод, что |
||||||||
касательные напряжения в точках поперечного сечения изменяются по |
||||||||
линейному |
закону. Наибольшие напряжения |
наблюдаются |
в точках, |
|||||
|
trdA |
|
принадлежащих |
внешнему |
контуру -се |
|||
Mz |
tmax |
чения. |
|
|
|
из усло- |
||
|
|
|
Найдем величину dj / dz |
|||||
|
r |
|
вия, что касательные напряжения, дейст- |
|||||
|
|
|
вующие по поперечному сечению вала, |
|||||
r |
dA |
x |
можно привести |
к |
паре сил, момент ко- |
|||
торой равен крутящему моменту Мz. Вы- |
||||||||
|
|
|
||||||
|
|
|
делим вокруг произвольной точки пло- |
|||||
|
y |
|
щадку dA, на которой действует элемен- |
|||||
|
|
тарная касательная |
сила t r dA (рис. 5.8). |
|||||
|
|
|
||||||
Рисунок 5.8 |
|
Запишем выражение для момента этой |
||||||
|
|
|
силы относительно оси вала |
|
|
|||
dM z =t r dAr ,
тогда полный крутящий момент равен:
M z = òòt r dAr . |
(5.13) |
А |
|
Подставляя в формулу (5.13) выражение (5.12), получаем
dj
M z = òòGr dz dAr .
А
Вынесем за знак интеграла величину G dj , так как для всех то- dz
чек поперечного сечения она является некоторой постоянной. В результате получаем
J r = òòr 2 dA ,
А
где Jr - полярный момент инерции поперечного сечения.
Для круглого поперечного сечения он равенJ r = pd 4  32 , а для кольцевого сечения - Jr = p (D4 - d 4 )
32 , а для кольцевого сечения - Jr = p (D4 - d 4 ) 32 .Отсюда
32 .Отсюда
dj M z = GJ r dz
128

или |
|
|
|
|
|
|
|
|
|
|
M z |
|
= |
dj |
. |
|
(5.14) |
||
|
|
|
|
|
|||||
|
GJ r |
|
dz |
|
|
||||
Подставляя полученное соотношение в формулу(5.12) оконча- |
|||||||||
тельно имеем |
|
|
|
|
|
|
|
|
|
|
t r |
= |
M z r |
|
. |
(5.15) |
|||
|
|
J r |
|||||||
|
|
|
|
|
|
|
|||
Это выражение позволяет определять касательные напряжения в любой точке круглого поперечного сечения. Максимальные напряжения t max определяют по формуле
t max |
= |
M z r |
= |
M z |
. |
(5.16) |
|
|
|||||
|
|
J r Wr |
|
|||
Величину Wr называют полярным моментом сопротивления. Для круг-
лого поперечного сечения Wr = pd 3 16 = pr3 2 .
Из уравнения (5.14) найдем полный угол закручивания вала jl
l |
l |
M z |
|
|
|
jl = òdj =ò |
dz . |
(5.17) |
|||
|
|||||
0 |
0 |
GJ r |
|
||
Если крутящий момент по длине вала и стержень имеет постоянный диаметр, тогда получаем
jl |
= |
M z l |
. |
(5.18) |
|
||||
|
|
GJ r |
|
|
Для ступенчатых валов, а также для валов постоянного сечения в случае скачкообразного изменения крутящего момента, угол закручивания находится как сумма углов закручивания по всем участкам
jl = |
n |
M zi li |
. |
(5.19) |
|
å= |
|
||||
|
GJ |
ri |
|
||
|
i 1 |
|
|
||
Величину GJr называют жесткостью стержня при кручении.
Она характеризует сопротивление вала закручиванию. Кроме того, для оценки жесткости вала используют параметр, называемый относи-
тельным углом закручивания
q = |
M z |
. |
(5.20) |
|
GJ r
129
