
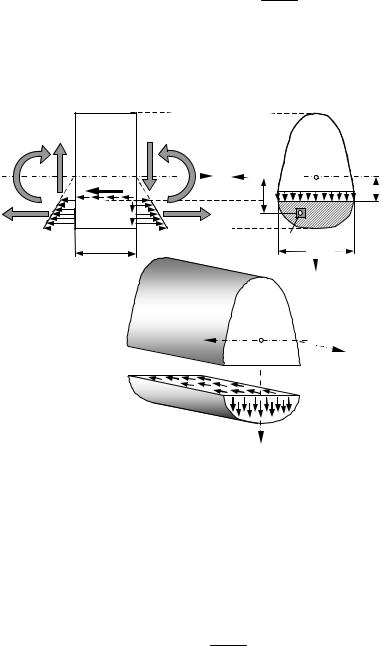
Здесь интегрирование производится по площади отсеченной части сечения Acut , которая заштрихована на рис. 7.5.
Интеграл в выражении(7.12) представляет собой статический момент отсеченной части сечения относительно оси Ох
Sxcut = òò y1dA .
Acut
Отсюда получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
dN z |
= dM x |
Sxcut . |
|
|
|
|
|
(7.13) |
|||
|
|
|
|
|
|
J x |
|
|
|
|
|
|
|
|
|
|
Чтобы равновесие нижней части элемента выполнялось, необхо- |
||||||||||||||
димо приложить к элементу дополнительную силу dТ , удерживающую |
|||||||||||||||
|
|
|
|
|
|
|
|
|
нижнюю отсеченную |
||||||
|
|
|
Qy |
|
|
|
|
|
часть |
от |
|
смещения |
|||
Mx |
Qy |
|
|
|
|
|
|
вдоль |
оси |
Oz . |
|
Эта |
|||
|
|
Mx+dMx |
|
|
|
|
сила связана с дейст- |
||||||||
|
|
|
|
z |
x |
|
O |
|
|||||||
|
|
|
|
|
|
вием |
касательных |
||||||||
|
|
dT |
|
|
1 |
|
tyz |
y |
|||||||
|
|
tyz t |
|
|
y |
|
|
|
напряжений t yz , |
воз- |
|||||
|
|
|
|
|
|
K |
|
||||||||
|
|
zy |
|
Nz+dNz |
|
|
|
никающих |
|
в |
|
гори- |
|||
Nz |
sz |
|
s +ds |
|
dA |
|
|
|
|||||||
dz |
|
b(y) |
|
зонтальном |
сечении. |
||||||||||
|
|
z |
z |
|
|
|
|||||||||
|
|
|
|
|
|
|
y |
|
Для |
|
большинства |
||||
|
|
|
|
|
|
|
|
|
поперечных |
|
сечений |
||||
|
|
|
|
|
|
|
|
|
делается допущение, |
||||||
|
|
|
|
x |
|
O |
|
|
что |
касательные |
на- |
||||
|
|
|
|
tyz |
|
z |
|
пряжения t yz |
равно- |
||||||
|
|
|
|
|
|
мерно |
распределены |
||||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
tzy |
|
по |
ширине |
|
горизон- |
||||
|
|
|
|
|
|
|
тального |
|
сечения. |
||||||
|
|
|
|
|
|
y |
|
|
|
||||||
|
|
|
|
|
|
|
|
Используя это |
допу- |
||||||
|
|
|
Рисунок 7.5 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
щение, |
определяем |
|||||||
|
|
|
|
|
|
|
|
|
силу dТ |
|
|
|
|
||
dТ =t zy b(y)dz , |
(7.14) |
где b(y) - ширина поперечного сечения в точке, где определяются касательные напряжения.
Приравнивая выражения (7.13) и (7.14), получаем
dM x Sxcut =t zy b(y )dz . J x
180
В соответствии с законом парности касательных напряжений обозначим t zy =t уz = t . Тогда
t = |
dM x |
× |
|
|
Sxcut |
. |
|
||||
|
|
dz |
|
|
J x b(y ) |
|
|||||
Как следует из дифференциального уравнения равновесия |
|
||||||||||
Qy |
= |
dM x |
. |
|
|||||||
|
|
|
|||||||||
|
|
|
|
|
|
dz |
|
||||
Окончательно получаем |
|
|
|
|
|
|
|
|
|
||
t = |
Q |
S cut |
|
||||||||
|
y |
|
x |
|
. |
|
|
(7.15) |
|||
|
|
|
|
|
|
|
|||||
|
|
J x b(y ) |
|
||||||||
Впервые эту формулу для определения касательных напряжений получил русский инженер Д.И. Журавский (1821 – 1892), поэтому ее называют формулой Журавского.
Проверка прочности балки по касательным напряжениям выполняется в сечениях, где возникает максимальная по модулю поперечная сила Qmax
tmax |
= |
Qmax Sx |
£ Rs , |
(7.16) |
|
||||
|
|
J xb |
|
|
где Rs - расчетное сопротивление материала.
Знак касательных напряжений соответствует знаку поперечной силы Qy в расчетном сечении балки.
§7.3 РАСПРЕДЕЛЕНИЕ КАСАТЕЛЬНЫХ НАПРЯЖЕНИЯ ПО ВЫСОТЕ ПОПЕРЕЧНОГО СЕЧЕНИЯ БАЛКИ
b
x |
|
O |
||
|
|
|
|
h |
h/2-y |
y |
|
h/4+y/2 |
|
|
|
|
|
|
|
|
|
O1 |
|
x1
y
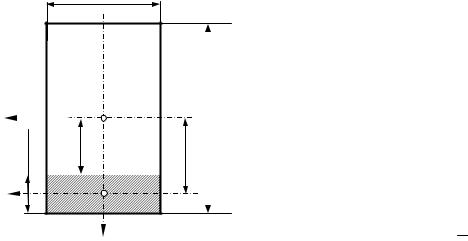
Рисунок 7.6

 tmax=3Q/2A
tmax=3Q/2A
Рассмотрим распределение касательных напряжений по высоте поперечных сечений
балки. |
Пусть |
задано |
прямо- |
|
угольное сечение балки(рис. |
||||
7.6) Проведем |
сечение |
парал- |
||
лельное |
оси Ох |
на |
расстоянии |
|
у. Ширина поперечного сечения |
||||
b(y)= b . |
Высота |
отсеченной |
||
части
h1 = h - y .
2
181

Площадь отсеченной части поперечного сечения |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ h |
|
|
|
ö |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
Acut |
= b × h1 |
= b ×ç |
|
|
|
- y ÷. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
||||||
Находим координату центра тяжести отсеченной части относи- |
|||||||||||||||||||||||||||||||||||||||
тельно оси Ох |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
h |
|
|
h |
|
|
|
1 æ h |
|
|
|
ö |
|
h |
|
|
|
y |
|
|
|
|
||||||||||||||
|
y = |
|
- |
|
1 |
= |
|
|
|
- |
|
|
ç |
|
|
|
- y ÷ = |
|
|
+ |
|
|
|
. |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
1 |
2 |
|
2 |
|
|
|
|
2 |
|
|
2 è 2 |
|
|
|
|
ø |
|
4 |
|
|
2 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Статический момент заштрихованной части сечения равен |
|||||||||||||||||||||||||||||||||||||||
cut |
|
|
|
|
æ h |
|
|
|
|
ö |
|
|
æ h |
|
|
|
|
y ö |
|
|
b |
|
æ h2 |
|
2 |
ö |
|||||||||||||
Sx |
= Acut × y1 = b ×ç |
|
|
|
- y ÷ × |
ç |
|
|
+ |
|
|
÷ |
= |
|
|
×ç |
|
|
- y |
|
÷. |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
4 |
|
||||||||||||||||||||||||||||
|
|
|
|
|
è 2 |
|
|
|
|
|
ø è 4 2 |
ø |
|
|
2 è |
|
|
|
ø |
||||||||||||||||||||
Момент |
инерции |
прямоугольного |
сечения |
|
относительно осиОх |
||||||||||||||||||||||||||||||||||
J x = bh3 12. Подставляя полученные выражения в уравнение (7.15), по- |
|||||||||||||||||||||||||||||||||||||||
лучаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6Qy |
|
|
æ h2 |
- y |
2 |
ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
t = |
|
|
|
|
|
|
|
×ç |
|
|
|
|
|
|
÷ . |
|
|
|
|
|
|
|
|
|
|
|
|
(7.17) |
|||||||||
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
bh |
|
|
ç |
|
4 |
|
|
|
|
|
|
|
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
è |
|
|
|
|
|
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Из выражения(7.17) следует, что касательные напряжения по высоте поперечного сечения изменяются по квадратной параболе. Максимальная величина касательных напряжений возникает на оси Ох (у = 0) и равны
tmax |
= |
3 |
× |
Qy |
= |
3 |
× |
Qy |
. |
(7.18) |
|
2 |
bh |
2 |
A |
||||||||
|
|
|
|
|
|
|
Касательные напряжения в крайних точках поперечного сечения балки (у = ± h/2) равны нулю.
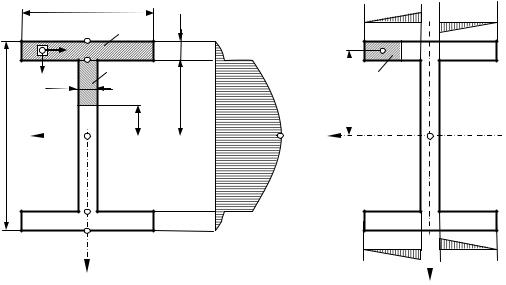
Далее рассмотрим двутавровое сечение. Особенностью такого сечения является резкое изменение ширины поперечного сечения в месте перехода полки в стенку. Заменим реальное двутавровое сечение приближенным, составленным из трех прямоугольников (рис. 7.7).
Проведем сечение параллельное оси Ох в точке перехода полки в стенку (точка 2). Статический момент верхней отсеченной части равен
|
|
|
|
æ h |
|
t |
ö |
|
b t |
× (h - t ). |
|
S cut = A y |
c |
= b t ×ç |
|
- |
|
÷ |
= |
1 |
|||
|
|
|
|||||||||
x |
1 |
1 |
è |
2 |
|
2 |
ø |
|
2 |
|
|
|
|
1 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
Подставляя полученное выражение в формулу(7.15), записываем следующие выражения для касательных напряжений в точке 2:
182
|
со стороны полки: t2 |
= |
Q |
S cut |
|||||
- |
|
max |
|
x |
|
; |
|||
|
J x b1 |
|
|||||||
|
|
|
|
|
|
|
|||
|
со стороны стенки: t |
2¢ = |
Q |
|
S cut |
||||
- |
max |
|
x |
. |
|||||
|
|
|
|||||||
|
|
|
|
J xb2 |
|||||
В числителе обоих выражений имеем одинаковые значения, но знаменатели будут различны. Ввиду того, что b1 >> b2 , то t 2¢ >>t 2 .
|
|
b1 |
|
|
tzx |
1 |
t |
|
A1 |
||
|
|
2 |
A2 |
tzy |
b2 |
|
|
|
|
||
|
|
|
1 |
|
|
|
у |
|
|
|
2 |
h |
|
3 |
у |
|
|
||
|
|
|
|
х |
|
|
|
|
|
4 |
|
|
|
5 |
|
|
|
у |
|
0 t2 t2¢
у′1
tmax
х
0 t4 t4¢
Эпюра t zy
Рисунок 7.7
A′1
у |
Эпюра tzх |
При определении касательных напряжений в полке двутавра - сле дует иметь ввиду, что в каждой ее точке возникают два касательных напряжения t zx и t zy . Касательные напряжения в полке t zy могут опре-
деляться по формуле (7.16) лишь приближенно, так как допущение о равномерном распределении касательных напряжений по ширине сечения не оправдывается. Однако, эти напряжения малы и практически не влияют на прочность сечения.
Рассмотрим сечение, проведенное в пределах стенки двутаврового сечения. Статический момент площади верхней отсеченной части сечения может быть найден как сумма статических моментов двух -за штрихованных площадей A1 и A2 :
Sxcut = A1 yc1 + A2 yc2 .
Эпюра касательных напряженийt zy в пределах стенки изменяется
по закону квадратной параболы. Максимальное значение касательных напряжений возникает в точках, принадлежащих оси Ох (рис. 7.7).
183

Рассмотрим горизонтальные касательные напряженияt |
. Если |
zx |
|
предположить, что по толщине полки эти напряжения распределены равномерно, то для их определения можно воспользоваться формулой (7.15). При этом статический момент вычисляется как произведение площади полки до рассматриваемого волокна на расстояние до центра тяжести этой площади до нейтральной осиSx¢1 = A1¢ × y1¢. Эпюры напряжений t zx показаны на рисунке 7.7.
§7.4 АНАЛИЗ НАПРЯЖЕННОГО СОСТОЯНИЯ ПРИ ПЛОСКОМ ИЗГИБЕ БАЛКИ
Как уже говорилось ранее, при поперечном изгибе в сечении балки возникают как нормальные, так и касательные напряжения. Следовательно, в произвольной точке балки имеет место плоское напряженное состояние. Введем следующие обозначения s = s z , t =t zy . Учиты-
вая, что продольные волокна балки не давят друг на друга, то s y = 0 . В
результате получаем
s1,3 |
= s ± 1 |
s 2 + 4t 2 и tg 2a0 |
= - |
2t |
. |
|
|||||
|
2 2 |
|
|
s |
|
Нормальные и касательные напряжения при изгибе определяются по выражениям (7.9) и (7.15)
s = |
M x |
y и t = |
Qy Sxcut |
. |
|
|
J x |
|
J x b(y ) |
|
|
Исследуем напряженное состояние в точках балки прямоугольно- |
|||||
го поперечного сечения, изменяя координату у (рис. 7.8). |
Будем счи- |
||||
тать, что поперечная сила Qy |
и изгибающий момент M x |
положитель- |
|||
ны, тогда искомые напряжения определяются следующим образом:
- точка 1: |
y |
= - |
h |
; |
S cut = 0 ; t |
1 |
= 0 ; s |
|
= -s |
max |
= - |
M x |
× |
h |
= - |
M x |
; |
|||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||
|
1 |
|
|
|
2 |
|
x1 |
|
|
|
|
|
|
|
|
|
|
J x |
2 |
|
|
Wx |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
s1,3 = -s ± 1 |
|
s 2 + 4 × 02 |
; s |
1 = 0 ; s |
3 |
= -s max ; |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tg 2a0 = - |
0 |
|
= 0 ; a0 = 0o ; a0¢ = 90o . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cut |
|
h |
|
|
h |
|
bh2 |
|
|
|
|
3 |
|
Qy |
|
|
|
|
|
||||
- точка 2: |
y2 |
= |
0 |
|
; Sx 2 |
= |
|
|
×b × |
|
|
|
= |
|
; |
t 2 =tmax = |
|
× |
|
|
|
; |
s = 0 ; |
|||||||||
|
2 |
|
4 |
8 |
2 |
|
A |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
184
s1,3 |
= - 0 ± 1 |
02 |
+ 4 ×tmax2 |
= ±t max ; s1 =t max ; s 3 |
= -tmax ; |
|
|
|
||||||||||||||||||||
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
tg 2a0 = - |
2t max |
= ¥ ; a0 = 45o ; a0¢ =135o . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- точка 3: y3 |
= |
h |
; |
Sxcut3 = 0 ; t3 |
= 0 ; s = smax |
= |
M x |
|
× |
h |
= |
M x |
; |
|
|
|||||||||||||
|
J x |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 Wx |
|
|
|
|||||
s1,3 |
= s ± 1 |
|
s 2 |
+ 4 ×02 ; |
s1 |
= s max ; s 3 = 0 ; |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
tg 2a0 = - |
|
0 |
|
= 0 ; a0 = 90o ; a0¢ = 0o . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
s1 = 0 |
|
1 s |
3 |
|
= s |
max |
|
|
s |
max |
|
|
|
0 |
|
|
|
s |
max |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
s 3 = s max |
|
s1 |
= 0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
- |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
s1 =tmax |
2 |
s3 |
|
=tmax |
0 |
|
+ t |
t max |
t |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
max |
|
|
|
|
|
max |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
s |
s1 =tmax |
3 =tmax |
s3 = 0
s1 = smax
|
|
+ |
|
+ |
s1 = smax |
0 |
|
||
3 |
|
s max |
s max |
0 |
|
Эпюра t |
Эпюра s1,3 |
||
s3 |
= 0 |
Эпюра s |
||
Рисунок 7.8
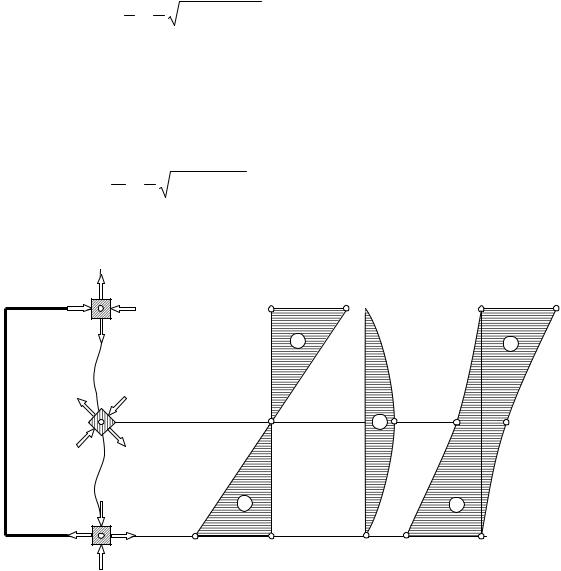
По полученным значениям можно построить эпюры распределения нормальных, касательных и главных напряжений по высоте поперечного сечения балки. Эти эпюры представлены на рисунке 7.8.
Рассмотрим построениетраекторий главных напряжений. Так называется линия, в каждой точке которой касательная совпадает с направлением главного напряжения, возникающего в исследуемой точке тела. Траектории главных напряжений зависят от типа нагрузки и способа опирания балки.
На рисунке7.9 показаны траектории главных напряжений, построенные для двух балок прямоугольного поперечного сечения(двухопорной и консольной). Траектории главных растягивающих напряже-
185

ний s1 |
показаны |
сплошными линиями, |
а |
траектории |
главных |
сжи- |
||||
мающих напряжений s3 |
- пунктирными. |
|
|
|
|
|
|
|
||
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
s3 |
s1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
s1 |
s3 |
|
|
z |
|
|
|
|
|
|
|
|
|
|
||
q/2 |
|
|
|
|
|
|
|
|
q/2 |
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
s1 |
|
s |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s |
s |
|
|
z |
|
|
|
|
|
|
1 |
|
|
|
||
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
Рисунок 7.9 |
|
|
|
|
|
|
|
По траекториямs1 можно судить о том, где и в каком направлении могут появиться трещины, если материал балки плохо работает на растяжение. При армировании изгибаемых железобетонных элементов арматуру целесообразно располагать в зонах и по направлению действия главных растягивающих напряжений. Однако это требование часто вступает в противоречие с принятой технологией изготовления железобетонных конструкций.
ПРИМЕР 7.1
Исходные данные задачи.
Для заданной двухопорной балки(рис. 7.10) из условия прочности подобрать необходимые размеры поперечного сечения балки шести типов при R=200 МПа. Определить наиболее экономичный тип поперечного сечения изгибаемой балки. Выполнить проверку этого сечения по максимальным касательным напряжениям приRs=100 МПа. В опасном сечении построить эпюры распределения нормальных, касательных и главных напряжений.
186

Решение задачи.
Определяем величину опорных реакций заданной балки:
åmA = 0 ; VB = -10 + 4 ×42 / 2 -10 ×2 - 20 ×1 - 20 = -4,5кН; 4
åmB = 0 ; VA = 20 + 4 ×42 / 2 -10×2 + 20 ×5 -10 = 30,5 кН. 4
Проверка:
åy = 0 ; VA -VB - F1 + F2 - q ×4 = 0 ; 30,5 - 4,5 - 20 +10 - 4 ×4 = 0,
следовательно, опорные реакции найдены верно.
Используя полученные значения опорных реакций, строим эпюры поперечных сил Qy и изгибающих моментов M x . Исходя из построен-
ных эпюр, определяем положение опасных сечений трех типов:
-сечение первого типа соответствует точке, где возникает максимальный по модулю изгибающий момент. В этом сечении действуют максимальные нормальные напряжения;
-сечение второго типа соответствует точке, где возникает максимальная по модулю поперечная сила. В этом сечении будут действуют максимальные касательные напряжения;
-сечение третьего типа соответствует точке, где возникают значительные изгибающие моменты и соответствующие им поперечные силы. В этом сечении строят эпюры распределения
главных напряжений по его высоте.
В рассматриваемом примере сечения всех трех типов находятся в точке, расположенной на бесконечно малом расстоянии левее опорыА. Величина внутренних усилий в этих сечениях равна: М х = -20 кНм и
Qy = -20кН.
Условие прочности при изгибе по максимальным нормальным напряжениям:
smax = M max £ R =160МПа.
Wx
Вычисляем требуемый момент сопротивления сечения балки:
W = |
M x ,max |
= |
20 ×103 |
= 125 ×10-6 м3 = 125см3. |
|
|
|
|
|||
nec |
R |
|
160 ×106 |
|
|
|
|
|
|||
Определяем размеры поперечных сечений заданных типов: - круглое поперечное сечение:
187

|
|
pd 3 |
|
|
|
|
|
|
|
|
32W |
|
|
|
|
32 |
×125 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Wx |
= |
|
|
|
|
|
|
dnec ³ 3 |
nec = 3 |
|
|
|
= 10,84 см, принимаем d = 109мм |
||||||||||||||||||||||||||||||||
32 |
|
|
3,14 |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A = |
pd 2 |
|
= |
3,14 ×10,92 |
= 93,27 см2; |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
I II |
III |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
М2=20кНм |
|
|
|
|||||||||||
|
|
|
|
|
|
|
F1=20кН |
|
М1=10кНм |
|
|
|
|
q=4кН/м |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
4 |
5 |
6 |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
z |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F2=10кН |
|
|
|
|
|
7 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
VB=4,5кН |
|
B |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
VA=30,5кН |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 м |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 м |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 м |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 м |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
y |
10,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2,5 |
|
|
|
|
|
|
|
|
4,5 |
|
|
Эп. Qy |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,0 |
0,0 |
|
(кН) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20,0 |
20,0 |
 20,0
20,0
10,0 |
0,0
3,0
Эп. Mх  (кН)
(кН)
20,0 |
20,0 |
Рисунок 7.10
- квадратное поперечное сечение:
W |
x |
= |
а3 |
a |
nec |
³ 3 6W = 3 |
6 ×125 = 9,09 см, принимаем a = 91мм |
|
|||||||
|
|
6 |
|
nec |
|
||
|
|
|
|
|
|
|
A= а 2 = 9,12 = 82,81см2;
-прямоугольное сечение с соотношением сторон h / b = 2 / 1:
|
|
|
bh2 |
|
4b3 |
|
|
6W |
6 |
×125 |
|
W |
x |
= |
|
= |
|
b |
³ 3 |
nec = 3 |
|
|
= 5,72 см, принимаем b = 58мм |
|
|
|
|
||||||||
|
|
6 |
|
6 |
nec |
|
4 |
|
4 |
|
|
|
|
|
|
|
|
|
|
h = 2 ×58 = 116 мм; A = ah = 5,8×11,6 = 67,28см2;
188

- прямоугольное сечение с соотношением сторон h / b = 3 / 1:
W |
x |
= |
bh 2 |
= |
9b3 |
b ³ 3 |
6W |
nec = 3 |
6 |
×125 |
= 4,37 см, принимаем b = 44 мм |
|
|
|
|
|
|||||||
|
|
6 |
|
6 |
nec |
9 |
|
9 |
|
||
|
|
|
|
|
|
|
|||||
h= 3×44 = 132 мм; A = ah = 4,4 ×13,2 = 58,08см2;
-сечение, составленное из двух швеллеров, сложенных полками:
|
|
Wx шв |
³ |
Wnec |
= |
125 |
= 62,5 см3, |
|
|
|||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|||
по сортаменту (ГОСТ 8240-89) принимаем швеллер №14 с Wшв = 70,2 |
||||||||||||||
см3 и А |
=15,6 см2. Общая площадь составного сечения |
|
|
|||||||||||
шв |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А =15,6 ×2 = 31,2 см2. |
|
|
|
|||||||||
- двутавровое сечение:W ³W |
|
=125 |
см3 , по |
сортаменту |
прокатной |
|||||||||
|
|
x |
|
nec |
|
|
|
|
|
№18 с Wх |
=143 |
3 |
||
стали (ГОСТ |
8239-89) принимаем |
двутавр |
||||||||||||
см, |
||||||||||||||
Ах = 23,4 |
2 |
Sx = 81,4 |
3 |
, |
|
|
|
4 |
, |
h =180мм, |
b = 90 мм, |
|||
см, |
см |
J x =1290 см |
||||||||||||
d = 5,1мм и t = 8,1мм.
Сравнивая площади подобранных сечений, приходим к выводу, что наиболее рациональным по расходу материала является двутавровое сечение, которое обладает минимальной площадью. Указанное сечение принимаем для дальнейших расчетов.
Используя формулу Журавского, проверяем подобранное двутавровое сечение по максимальным касательным напряжениям:
t |
|
= |
Qmax Sхотс,max |
= |
|
20 ×103 ×81,4 × |
10-6 |
= 24,75 |
МПа < R |
s |
= 100 МПа. |
|
max |
J x b |
1290 ×10-8 ×5,1 |
×10-3 |
|||||||||
|
|
|
|
|
|
|||||||
Следовательно, условие прочности сечения по максимальным касательным напряжениям выполняется.
Строим эпюры распределения нормальных, касательных и главных напряжений по высоте сечения по формулам:
|
|
M x × y(i ) |
|
|
|
Q × Sx(i ) |
; |
s(i ) |
|
1 |
2 |
2 |
||||
s(i ) |
= |
|
|
|
|
; t(i ) = |
|
s1,3(i ) = |
|
± |
|
s(i ) + 4t(i ). |
||||
J x |
J x ×b(i ) |
|
|
|||||||||||||
|
|
|
|
|
|
2 2 |
|
|
||||||||
Построения ведем |
для опасного |
сечения третьего |
типа, для |
которого |
||||||||||||
М х = -20 кНм и Qy |
= -20кН. Напряжения вычисляем в точках 1-7 дву- |
|||||||||||||||
таврового сечения (рис. 7.11). |
|
|
|
|
|
|
|
|||||||||
Точка 1: |
y(1 ) = - |
h |
= - |
18 |
= -9 см; |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||||||
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|||
189
