

|
|
а=0,5 м |
|
у |
а=0,5 м |
R=160МПа; |
|
|
|
|
|
|
n=1,5; |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l =1,5 ´10-5 град-1; |
|
В |
м |
|
|
|
|
K |
Dt = -50o ; |
|
|
h=0,2 |
1 |
|
b |
O |
5 |
d1 = -0,1см; |
|
|
|
d2 = 0,2 см; |
|
|||||
|
|
|
|
|
|
|
||
|
м |
2 |
|
a |
|
4 |
A1 A2 = m1 = 2 ; |
|
|
h=0,2 |
|
|
|
A1 = A5; A2 = A4; |
|||
|
|
|
|
|
|
|||
|
С |
|
F=50 кН |
D |
F = 50 кН; |
|
||
|
|
|
|
|||||
|
|
|
|
|
|
|
a = 0,5 м; |
|
|
|
|
b=0,3 м |
|
b=0,3 м |
h = 0,2 м; |
|
|
|
|
|
Рисунок 3.32 |
E = 2 ×105 МПа. |
|
|||
|
|
|
|
|
||||
|
Решение задачи. |
|
|
|
|
|||
|
а) Статическая сторона задачи. |
|
|
|||||
|
Из симметрии системы относительно вертикальной оси следует, |
|||||||
что N1=N5 и N2=N4, |
следовательно, имеется две неизвестных величины: |
|||||||
|
N1 |
|
у |
N5=N1 |
|
N1 и N2. Для нахождения этих величин рас- |
||
|
|
|
смотреть равновесие |
отсечённого |
узлаО |
|||
|
|
|
|
|
||||
|
|
b |
O |
|
|
(рис. 3.33). Для плоской системы силN1, |
||
|
|
a |
|
|
|
N2, N4, N5 и F, сходящейся в одной точке, |
||
|
|
|
|
|
можно составить два независимых уравне- |
|||
|
|
|
|
|
|
|||
|
|
|
|
|
|
ния равновесия. Если же система симмет- |
||
|
N2 |
|
F |
N4=N2 |
|
рична относительно вертикальной осиОу, |
||
|
|
Рисунок 3.33 |
|
|
то остаётся одно независимое уравнение: |
|||
å у = 0 ; 2N1 cos b - 2N2 cosa - F = 0 .
Далее вычисляем
a = arctg |
b |
= arctg |
0,3 |
= 56,31o ; b = arctg |
a |
= arctg |
0,5 |
= 68,2o . |
h |
|
h |
|
|||||
|
0,2 |
|
0,2 |
|
||||
Подставив значения тригонометрических функций углов a и b в уравнение статики, получаем:
-1,109N2 + 0,743N1 = 50000 . |
(3.22) |
Так как рассмотрение статической стороны задачи |
даёт одно |
уравнение с двумя неизвестными, то задача является статически неопределимой.
б) Геометрическая сторона задачи.
Рассмотрим какое-либо малое перемещение узла О, не нарушающее симметрии стержневой системы(рис. 3.34). Очевидно, что ввиду симметрии системы это вертикальное малое перемещение. Так как стержни 1, 2, 4 и 5 остаются соединёнными в узлеО, а вторые концы
91
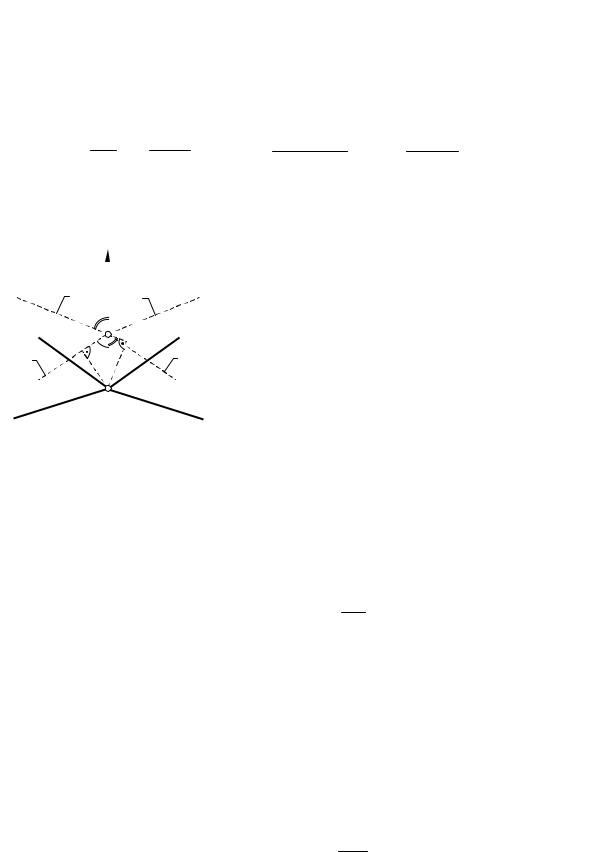
этих стержней неподвижны, то их удлинения можно связать математи- |
||||||||||||||
ческим выражением. Вследствие малости перемещения OO¢ новое по- |
||||||||||||||
ложение стержня практически является параллельным исходному -по |
||||||||||||||
ложению. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
|
¢¢¢ |
|
¢ |
cos b ; |
* |
|
¢¢ |
|
¢ |
cosa ; |
||
|
Dl1 |
= O O |
= OO |
Dl2 = OO |
|
= OO |
||||||||
Dl |
* |
|
cos b |
; |
Dl* = - |
cos 68,2o |
Dl* |
= - |
0,3714 |
Dl* ; |
||||
1 = - |
|
|
|
|
|
|||||||||
Dl2* |
|
cosa |
|
1 |
|
cos 56,31o |
2 |
|
0,5547 |
2 |
||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
Dl* = -0,6695Dl |
* . |
|
|
|
|
(3.23) |
|||
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь знак «минус» учитывает, что |
|||||||
|
у |
|
|
|
один из стержней системы растягивается, а |
|||||||||
|
|
|
|
|
другой - сжимается. |
|
|
|
||||||
1 |
5 |
|
|
|
|
Следует отметить, что точка О явля- |
||||||||
b |
O |
|
|
|
ется проектным положением узла при от- |
|||||||||
O¢¢ |
b |
O¢¢¢ |
|
сутствии |
силы F, точном |
изготовлении |
||||||||
a |
|
4 |
|
всех стержней и предполагаемой темпера- |
||||||||||
2 |
|
|
|
|||||||||||
|
|
|
|
|
туре |
монтажа. |
Точка |
O¢соответствует по- |
||||||
O¢ |
|
|
|
ложению узла О при нагружении системы |
||||||||||
Рисунок 3.34 |
|
заданной нагрузкой F, при действии задан- |
||||||||||||
|
ного температурного перепада и неточно- |
|||||||||||||
|
|
|
|
|
сти изготовления ее отдельных элементов. |
|||||||||
в) Физическая сторона задачи. |
|
|
|
|
|
|
|
|||||||
Длина стержня может изменяться под действием следующих трёх |
||||||||||||||
факторов: неточности изготовления отдельных элементов, изменения |
||||||||||||||
температуры и при действии продольной силы. Удлинение стержня при |
||||||||||||||
действии всех этих факторов определяется следующим образом |
||||||||||||||
Dl* = d + at lDt + Nl EA
где d - неточность изготовления;
Dt - изменение температуры относительно исходной;
at - коэффициент линейного расширения материала стержня; l - длина стержня;
N - продольная сила;
A - площадь поперечного сечения;
E - модуль продольной упругости материала стержня. Для стержней рассматриваемой системы имеем:
Dl1* = d1 + atl1Dl + N1l1 ;
EA1
92

Dl2* = d2 |
+ at l2 Dl + |
N2l2 |
. |
(3.24) |
|
||||
|
|
EA2 |
|
|
где l1 =  a2 + h2 =
a2 + h2 =  0,52 + 0,22 = 0,538 м;
0,52 + 0,22 = 0,538 м;
l2 =  b2 + h2 =
b2 + h2 =  0,32 + 0,22 = 0,36 м.
0,32 + 0,22 = 0,36 м.
Подставляя выражение (3.23) в равенство (3.22) получаем:
|
+ at l1Dl + |
N1l1 |
é |
|
+ at l2 Dl + |
N2l2 |
ù |
|
|
d1 |
= -0,6695êd |
2 |
ú . |
(3.25) |
|||||
EA1 |
EA2 |
||||||||
|
|
ë |
|
|
û |
|
После численной подстановки заданных величин, имеем:
é |
|
- |
|
|
|
|
|
- |
|
|
|
|
N |
× 0,538 |
ù |
|
||||
ê-1 |
×10 |
|
3 +1,5 ×10 |
|
5 ×0,538 × (-50) + |
|
1 |
|
|
|
|
ú = |
|
|||||||
|
|
2 ×10 |
11 |
× 2 |
× A2 |
|
||||||||||||||
ë |
|
|
|
|
|
|
|
|
|
|
|
|
|
û |
|
|||||
|
|
|
é |
|
- |
3 |
|
|
|
- |
|
|
|
|
|
N |
2 |
×0,36 |
ù |
|
= -0,6695 × ê2 |
×10 |
|
+1,5 ×10 |
|
5 ×0,36 |
× (-50) + |
|
|
|
ú . |
||||||||||
|
|
|
|
|
11 |
× A2 |
||||||||||||||
|
|
|
ë |
|
|
|
|
|
|
|
|
|
|
|
|
2 ×10 |
û |
|||
После некоторых упрощений, получим:
-1,4035 +1,345 ×10-9 × |
N1 |
= -1,157 -1,2042 ×10-9 × |
N2 |
. |
(3.26) |
A2 |
|
||||
|
|
A2 |
|
||
Уравнения (3.22) и (3.26) представляют собой систему из двух линейных алгебраических уравнений с двумя неизвестными. Здесь А2 является некоторый параметром, который мы определим позже.
Чтобы решить систему, выразим N1 из (3.22):
N1=67295+1,4926N2.
Подставим это выражение в уравнение (3.26)
1,345 ×10-9 × (67295 +1,4926N2 ) +1,2042 ×10-9 × N2 = 0,2465A2 .
Отсюда получаем:
N |
2 |
= 7,675 ×10 |
7 × A - 28182; |
(3.27) |
|
|
2 |
||
N |
|
=1,1456 ×108 × A + 25180. |
||
1 |
|
|||
|
|
2 |
|
|
Для вычисления требуемой площади поперечного сеченияА2 необходимо воспользоваться условием прочности:
ì |
|
s |
1 |
£ R =160 ×106 |
; |
ï |
|
|
|
(3.28) |
|
í |
|
s |
|
|
|
ï |
|
|
£ R = 160 ×106. |
||
î |
|
|
2 |
|
|
|
|
|
|
||
93

Из полученной системы следует, что во всех стержнях нормальные напряжения по модулю не должны превышать величины расчётного -со противления материала стержня.
Чтобы воспользоваться условиями прочности, вычислим напряжения по известным из системы (3.28) продольным силам.
s1 |
= |
N1 |
|
= |
|
N1 |
= |
|
N1 |
|
= |
12590 |
+ 5,728 ×107 ; |
||
A1 |
m1 A2 |
2A2 |
|
|
|||||||||||
|
|
|
|
|
|
A2 |
|||||||||
|
|
s1 |
= |
N2 |
= - |
28182 |
+ 7,675 ×107 . |
||||||||
|
|
|
|
||||||||||||
|
|
|
|
|
|
A2 |
|
|
A2 |
|
|
|
|
||
Подставим найденные значения в систему неравенств (3.28)
ì |
12590 |
+ 5,728 ×107 |
£160 ×106 ; |
|
|
|||||||
|
|
|
|
|||||||||
ï |
|
A |
|
|
|
|
|
|
|
|
||
ï |
|
2 |
|
|
|
|
|
|
|
|
|
|
í |
|
28182 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||||
ï |
- |
+ 7,675 |
×10 |
7 |
£ 160 |
×10 |
6 |
. |
||||
ï |
|
A2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||
î |
|
|
|
|
|
|
|
|
|
|
||
Из первого неравенства системы получаем A2 ³1,226 ×10-4 м2. Второе неравенство системы уравнений (3.28) распадается на два
неравенства:
- |
28182 |
+ 7,675 ×107 |
£160 ×106 Þ - |
28182 |
£ 8,325 |
×10 |
7 ; A ³ 0 |
, |
|
|
|||||||
|
A2 |
|
A2 |
|
2 |
|
||
|
|
|
|
|
||||
т.к. в заданной задаче отрицательная площадь невозможна.
- |
28182 |
- 7,675 ×107 |
£160 ×106 ; |
28182 |
£ 236,7 |
×106 ; A ³1,191×10-4 |
м2. |
|
|
||||||
|
A2 |
|
A2 |
2 |
|
||
|
|
|
|
||||
Окончательно имеем следующую систему неравенств, эквивалентную исходной системе (3.28), т.е. условиям прочности:
ìïA2 ³1,226 ×10-4 м2 ;
íA2 ³ 0;
ïîA2 ³1,919 ×10-4 м2 .
Окончательно принимаем A2 =1,226 ×10-4 м 2 .
Выполняем проверку полученного решения, для чего следует установить выполняются ли условия прочности(3.28), уравнения равновесия (3.22) и геометрическое соотношение (3.23) с учётом физических соотношений (3.24). Вначале вычислим N1 и N2 по формулам (3.27):
94

N1 = 25180 +1,1456 ×108 ×1,226 ×10-4 = 39225 Н = 39,225 кН;
N2 = -28182 + 7,675 ×107 ×1,226 ×10-4 = -18772 Н = -18,772 кН.
Определяем напряжения в стержнях:
A1 = m1 A2 = 2 ×1,226 ×10-4 = 2,452 ×10-4 м2;
s |
|
= |
N1 |
|
= |
|
39225 |
|
|
= 159,97 МПа; |
||||
1 |
A |
|
|
|
|
|
||||||||
|
|
|
|
2,452 ×10 |
-4 |
|
|
|||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|||
s |
|
= |
N2 |
|
= - |
|
18772 |
|
|
= -153,11 МПа |
||||
2 |
A |
1,226 ×10-4 |
|
|||||||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||
Следовательно, условия прочности (3.28) выполняются. Подставим N1 и N2 в уравнение равновесия (3.22):
-1,109 × (-18772) + 0,743 ×39225 - 50000 = 49962 - 50000 = -38Н.
Если N1 и N2 найдены точно, то в правой части равенства(3.22) должен быть ноль, следовательно, погрешность решения равна:
49962 - 50000 ´100% = 0,076% .
50000
Вычислим теперь величины Dl1* и Dl2* по формулам (3.24)
Dl* |
= d |
1 |
+ a l Dl + |
|
N1l1 |
= |
|
|
||||
|
|
|
||||||||||
1 |
|
t 1 |
|
|
EA1 |
|
||||||
|
|
|
|
|
|
|
|
|
||||
= -1×10-3 +1,5 ×10-5 × 0,538 × (-50) + |
|
|
39225 × 0,538 |
|
= -9,732 ×10-4 м; |
|||||||
|
×1011 × 2,452 ×10-4 |
|||||||||||
|
|
|
2 |
|
||||||||
Dl2* = d2 + at l2 Dl + |
N2l2 |
= |
|
|
||||||||
|
|
|||||||||||
|
|
|
|
|
|
|
|
EA2 |
|
|||
= 2 ×10-3 +1,5 ×10-5 × 0,36 × (-50) + |
|
|
-18772 × 0,36 |
|
= 1,455 ×10-3 м. |
|||||||
|
|
×1011 ×1,226 ×10-4 |
|
|||||||||
|
|
|
2 |
|
|
|||||||
Проверим, выполняется ли геометрическое соотношение (3.23)
-9,732 ×10-4 = -0,6695 ×1,455 ×10-3 ;
-9,732 ×10-4 = -9,737 ×10-4 .
Погрешность этого равенства: 9,737 - 9,732 ×100% = 0,05% . 9,732
95
ПРИМЕР 3.5
Исходные данные задачи.
Выполним расчет статически неопределимой стержневой системы, рассмотренной в примере 3.4, по методу разрушающих нагрузок.
Решение задачи.
Так как проектная(допустимая) нагрузка, действующая на рассматриваемую стержневую систему, задана равной F = 50 кН, то разрушающая нагрузка с учетом коэффициента запаса n =1,5 определяется следующим образом
Fразр = n × F =1,5 × 50 = 75 кН.
Заданная геометрически неизменяемая стержневая система превратится в механизм, когда напряжение во всех ее стержнях будет по абсолютной величине равно пределу текучести s y . Так как сила F дей-
ствует вниз, и другие факторы в этом методе не учитываются, то точка О (рис. 3.32) при нагружении сместится вниз. При таком перемещении узла О стержни 1 и 5 будут растянуты, а стержни 2 и 4 - сжаты.
Запишем уравнение равновесия:
å у = 0 ; 2N1 × cos b + 2N2 × cosa = F ;
0,743N1 -1,109N2 = F .
Из условия превращения заданной системы в механизм следует, что при F = Fразр
N1 = s y × A1 ; |
N2 = -s y × A2 . |
Тогда из уравнения равновесия получаем
0,743×s y × A1 +1,109 ×s y × A2 = Fразр ;
0,743×s y × m1 × A2 +1,109 ×s y × A2 = Fразр ;
0,743×s y × 2 ´ A2 +1,109 ×s y × A2 = Fразр .
Учитывая, что для малоуглеродистой пластичной стали предел текучести равен s y = 240 МПа, имеем
A = |
Fразр |
= 1,204 ×10-4 м2. |
|
(0,743× 240 ×106 × 2 +1,109 × 240 ×106 ) |
|||
2 |
|
96
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ К ГЛАВЕ 3
1.По какой формуле вычисляются нормальные напряжения при одноосном растяжении или сжатии?
2.Как определяется относительная продольная деформация?
3.Что называется коэффициентом Пуассона?
4.В какой форме можно записать закон Гука?
5.Что называется модулем упругости первого рода (модулем Юнга)?
6.По каким площадкам бруса, работающего на одноосное растяжение, действуют максимальные касательные напряжения?
7.Какие испытательные машины используют для испытаний материалов на прочность?
8.Каковы соотношения размеров стандартных образцов, используемых для испытаний на растяжение и сжатие?
9.Какой вид имеет диаграмма растяжения малоуглеродистой стали?
10.Перечислите основные участки диаграммы растяжения стали.
11.Что называется пределом пропорциональности, пределом упругости, пределом текучести и пределом прочности?
12.Какие характеристики вязкости определяют при испытании стали на растяжение?
13.Какие величины относятся к прочностным характеристикам материала?
14.Что называют характеристиками пластичности материала?
15.Какой вид имеют диаграммы условных напряжений и истинных напряжений для растяжения низкоуглеродистой стали?
16.Что называется упругой и остаточной деформацией?
17.Какое явление называется наклёпом?
18.Какой вид имеет диаграмма растяжения чугуна?
19.Как деформируется стальной образец при испытании на сжатие?
20.Покажите вид диаграммы сжатия стали.
21.Какой вид имеет диаграмма сжатия чугуна?
22.Какую форму приобретает чугунный образец перед разрушением? Почему образец становится таким?
23.Какова причина появления трещин в чугунном образце при сжатии?
24.Как выглядят диаграммы деформирования линейно-упругих и -не линейно-упругих хрупких материалов?
25.Что называется секущим и касательным модулями упругости?
26.Каков характер деформирования и разрушения бетонного образца при наличии и при отсутствии сил трения между торцами образца и плитами пресса?
27.Какие факторы влияют на коэффициент запаса в расчетах по допускаемым напряжениям?
97
28.Как выбирают величину допускаемого напряжения?
29.В чем заключается метод расчета по разрушающим нагрузкам?
30.Что называется диаграммой Прандтля?
31.Какие группы предельных состояний Вы знаете?
32.В чем суть метода расчета по предельным состояниям?
33.Какие инженерные конструкции выгоднее с точки зрения расхода материалов?
34.Какие основные характеристики статически неопределимых систем Вы знаете?
35.По какому алгоритму выполняют расчет статически неопределимых систем, работающих на одноосное растяжение или сжатие?
98
ГЛАВА 4.
ДВУХОСНОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ В ТОЧКЕ ТЕЛА
§ 4.1. ПОНЯТИЕ О НАПРЯЖЕННОМ СОСТОЯНИИ В ТОЧКЕ ТЕЛА
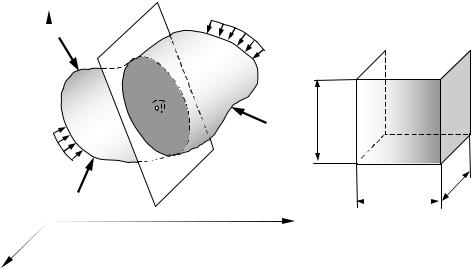
Напряженным состоянием в точке твердого деформируемого тела называют совокупность напряжений, действующих по всевозможным площадкам, проведенным через эту точку. В общем случае в теле напряженное состояние неоднородно - оно меняется от точки к точке и поэтому по любому сечению этого телаA напряжения распределены неравномерно. Для изучения напряженного состояния в какой-либо точке K мысленно вырезают в ее окрестности параллелепипед со сторонами dx, dy и dz (рис. 4.1). Ввиду малости элементарного параллелепипеда можно считать, что напряжения по его граням и по любым наклонным сечениям распределены равномерно. Напряжения на гранях параллелепипеда при этом считаются заданными, а напряжения, действующие в его наклонных площадках, определяют с помощью метода сечений из условий равновесия отсеченной части параллелепипеда.
y |
F2 |
|
q2 |
|
|
||
|
|
K |
|
|
|
|
dy |
|
|
A |
F3 |
|
|
|
|
|
q1 |
|
dx |
|
F1 |
|
dz |
0 
z
x
Рисунок 4.1
В любой точке нагруженного тела всегда можно выделить -эле ментарный параллелепипед, ориентированный так, что все его грани будут свободны от касательных напряжений. При этом различают линейное, плоское и объемное напряженные состояния в точке(рис. 4.2). Линейное напряженное состояние, например, испытывают точки бруса при центральном растяжении или сжатии. Плоское напряженное состояние наиболее часто встречается в задачах сопротивления материалов. Его характерным признаком является отсутствие каких-либо -на пряжений на двух параллельных гранях параллелепипеда. В таких условиях находятся, например, элементы стержней и балок, изготовлен-
98

ных из относительно тонких пластинок. Когда по всем граням элементарного объема действуют напряжения, то говорят об объемном напряженном состоянии в точке тела.
Иногда указанные виды напряженных состояний называют соответственно одноосным, двухосным или трехосным.
|
|
s2 |
|
|
s |
|
|
|
|
|
2 |
|
|
|
|
|
s3 |
s1 |
s |
s1 |
s1 |
s1 s |
s1 |
|
1 |
|
|
3 |
|
|
|
s2 |
|
|
s |
|
|
|
|
|
2 |
а) |
|
б) |
|
|
в) |
Рисунок 4.2
а) линейное напряженное состояние; б) плоское напряженное состояние; в) объемное напряженное состояние.
§ 4.2. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
Рассмотрим элементарный объем тела в плоском напряженном состоянии (рис. 4.3). В общем случае на гранях элементарного паралле-
лепипеда действуют нормальные напряжения s y и s х , |
а |
также |
каса- |
|||||
y |
|
тельные |
напряжения t yх |
и t хy . |
Так |
|||
sy |
|
как во всех точках элементарного |
||||||
tyх |
|
объема напряженное состояние |
счи- |
|||||
|
тается однородным, то одноименные |
|||||||
tzy |
|
|||||||
|
|
напряжения на |
параллельных гранях |
|||||
sх |
х |
должны |
равняться друг |
другу. При |
||||
анализе напряженного состояния ис- |
||||||||
sх tхy |
|
|||||||
tyх |
|
пользуют следующие правила обо- |
||||||
sy |
|
значения |
напряжений. |
Нормальные |
||||
|
напряжения имеют один индекс. Он |
|||||||
|
|
|||||||
Рисунок 4.3 |
|
показывает направление нормального |
||||||
|
напряжения |
относительно |
коорди- |
|||||
|
|
|||||||
натных осей. Для обозначения касательного напряжения используют два индекса, например tху. Здесь первый индекс показывает, что данное касательное напряжение действует на площадке с нормалью, парал-
99
