Техническая механика / 4_Tekhnicheskaya_mekhanika_dlya_stroiteley

ров. Справедливо и другое определение: эпюрой называется график,

показывающий изменение внутренних силовых факторов при перемещении поперечного сечения вдоль оси бруса при неизменной внешней нагрузке.

Построение эпюр внутренних силовых факторов необходимо для выполнения прочностных расчетов (подбора необходимых размеров поперечного сечения бруса из условий прочности при соответствую-

щих видах его деформации). Эпюры помогают установить положение «опасных» сечений, где возникают максимальные значения внутренних усилий и, следовательно, действуют экстремальные нормальные или касательные напряжения. Построение эпюр ведется известным методом сечений.

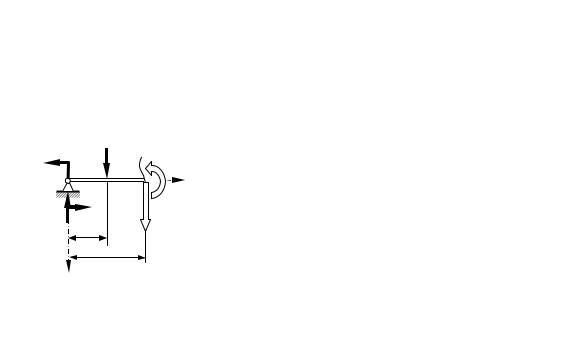
Введем следующие правила для определения знаков внутренних силовых факторов (рис. 6.5) для наиболее частого случая загружения бруса, когда все нагрузки приложены в вертикальной плоскости. Таким

Qy должна вращать рассматриваемую часть бруса по часовой стрелке и совпадает с положительным направлением осиOy. Изгибающий момент Mx будет считаться положительным, если растягивает нижние волокна бруса.

Эпюры строятся на оси бруса и заштриховываются перпендикулярно нулевой линии. Внутри каждой эпюры, за исключением эпюр изгибающих моментов, ставится соответствующий знак, который обычно обводится небольшой окружностью. Ординаты эпюр изгибающих моментов откладываются со стороны растянутых волокон бруса. Данное правило справедливо для всех строительных специальностей. Для всех других специальностей ординаты эпюр изгибающих моментов откладываются со стороны сжатых волокон бруса. Знаки на эпюрах изгибающих моментов обычно не ставят.

Приступая к построению эпюр внутренних силовых факторов, брус разбивают на грузовые участки. Грузовым участком называют часть оси бруса, заключенную:

-между точками приложения внешних сосредоточенных сил или моментов, включая опорные реакции;

-между точками, ограничивающими участки приложения распределенных нагрузок или моментов;

140

-между точками, где происходит излом оси бруса или изменяются размеры его поперечного сечения.

В пределах каждого грузового участка функции внутренних -си ловых факторов не должны иметь изломов или разрывов, т.е. в указанных пределах они являются гладкими, дифференцируемыми и интегрируемыми функциями.

§ 6.3 ОБЩИЙ ПОРЯДОК ПОСТРОЕНИЯ ЭПЮР ВНУТРЕННИХ

чении. Для их определения используют уравнения статики. Порядок построения эпюр внутренних силовых факторов рассмотрим на -сле дующем примере.

ПРИМЕР 6.1

Исходные данные задачи.

Для заданной двухопорной балки (рис. 6.6) построить эпюры поперечных сил Qy и изгибающих моментов M x .

Решение задачи.

Определяем величину опорных реакций балки(рис. 6.6), возникающих от действия внешних нагрузок:

141

Положительные значения эпюры Qy откладываем выше нулевой линии. Эпюра изгибающих моментов M x отрицательна в пределах все-

142

å y = 0 ; Qy - RA + F = 0 ; Qy = RA - F =12 -10 = 2 кН = сonst ;

åmx = 0 ; M x - RA × z2 + M1 + F (z2 -1)= 0 ; M x = RA × z2 - M1 - F (z2 -1).

Из полученных выражений следует, что эпюра поперечных сил Qy в пределах второго грузового участка представляет собой прямую,

параллельную горизонтальной оси и не зависит от текущей координаты z , а эпюра изгибающих моментов M x линейно зависит от координаты z . Для построения эпюры M x достаточно определить ее ординаты на границах грузового участка:

Строим эпюры Qy и M x в пределах второго участка (рис. 6.6).

Анализируя ранее выполненные расчеты можно сделать вывод, что при увеличении количества грузовых участков от начала координат до рассматриваемого сечения запись уравнений статики значительно усложняется. Поэтому при построении эпюр внутренних силовых факторов часто применяют такой прием как изменение начала координат. Это помогает существенно уменьшить трудоемкость вычислений.

Рассмотрим поперечное сечение балки, проведенное в пределах четвертого грузового участка (рис. 6.9). Начало координат располагаем в крайней правой точке балки. Ось z направляем вдоль оси балки, ось x

143

- навстречу нашему взгляду, а ось y направляем вверх, чтобы получить правостороннюю систему координат. Отбрасываем левую часть балки. В сечении показываем внутренние силовые факторы(изгибающий момент Mx и поперечную силу Qy), действующие в положительном направлении. Координата z4, определяющая положение рассматриваемого

веденное в пределах третьего грузового участка(рис. 6.10). Начало координат оставляем в крайней правой точке балки. Ось z направляем вдоль оси балки, ось x - навстречу нашему взгляду, а ось y направляем

åy = 0 ; Qy + RB - q(z3 -1)= 0 ; Qy = q(z3 -1)- RB ;

åmx = 0 ; M x + M 2 - RB (z3 -1)+ q(z3 -1)2 / 2 = 0 ;

M x = RB (z3 -1)- M 2 - q(z3 -1)2 / 2 .

Из полученных выражений следует, что эпюра поперечных сил Qy в пределах третьего грузового участка изменяется по линейному за-

144

кону, а эпюра изгибающих моментов M x зависит от квадрата координаты z и представляет собой квадратную параболу. Строим эпюры Qy и M x в пределах четвертого грузового участка (рис. 6.6). Для построения эпюр Qy и M x необходимо определить их ординаты на границах грузового участка:

z3 =1 м; Qy = q(z3 -1)- RB = 4(1 -1)- 6 = -6 кН;

M x = RB (z3 -1)- M 2 - q(z3 -1)2 / 2 = 6(1 -1)-10 - q(1 -1)2 / 2 = -10 кНм. z3 = 3 м; Qy = q(z3 -1)- RB = 4(3 -1)- 6 = 2 кН;

M x = RB (z3 -1)- M 2 - q(z3 -1)2 / 2 = 6(3 -1)-10 - 4(3 -1)2 / 2 = -6 кНм.

Исходя из полученных значений видно, что эпюра Qy в пределах

третьего грузового участка меняет знак и пересекает нулевую линию. Как будет доказано далее под нулевым значением на эпюре поперечных сил Qy на эпюре изгибающих моментовM x имеется экстремум. Ис-

пользуя простейшие геометрические соотношения можно установить, что нулевая точка эпюры Qy находится на расстоянии z3 = 2,5 м от на-

чала координат. Вычисляем величину внутренних силовых факторов в указанном сечении:

z3 = 2,5 м; Qy = q(z3 -1)- RB = 4(2,5 -1)- 6 = 0 ;

M x = RB (z3 -1)- M 2 - q(z3 -1)2 / 2 =

= 6(2,5 -1)-10 - 4(2,5 -1)2 / 2 = -5,5кНм.

По полученным значениям строим эпюрыQy и M x в пределах

третьего грузового участка (рис. 6.6). таким образом мы рассмотрели все грузовые участки заданной балки и получили окончательный вид эпюр поперечных сил Qy и изгибающих моментов M x .

§6.4 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ РАВНОВЕСИЯ БРУСА

СПРЯМОЛИНЕЙНОЙ ОСЬЮ

Если внешние нагрузки, действующие на брус и все реакции в его связях (опорные реакции) известны, то внутренние усилия можно определить из уравнений статики, рассматривая равновесие отсеченной части бруса. Выделим из бруса элементарную часть, ограниченную двумя поперечными сечениями, проведенными на расстоянии z и z+dz от начала координат (рис. 6.11). Брус считаем загруженным погонной распределенной нагрузкой q, погонным распределенным моментом m, не-

145

åz = 0; - N z + (N z + dN z )+ qz dz = 0;

åy = 0; - Qy + (Qy + dQy )+ qy dz = 0;

åmxB = 0; -M x + (M x + dM x )- Qy dz + qy dz(dz / 2)+ mx dz = 0.

Пренебрегая слагаемым второго порядка малости в третьем уравненииполучаем дифференциальные уравнения равновесия бруса для плоскости zOy.

Если изгибная деформация бруса происходит в двух главных плоскостях инерции, то необходимо рассмотреть равновесие выделен-

146

ного элемента в плоскости zOх. По аналогии с вышеизложенным запишем следующие уравнения статики:

åx = 0; - Qx + (Qx + dQx )+ qx dz = 0;

åmyB = 0; -M y + (M y + dM y )- Qx dz + qx dz(dz / 2)+ my dz = 0.

Следовательно,

Последнее, шестое, уравнение равновесия получим из суммы моментов относительно оси Oz:

åmx = 0; - M x + (M x + dM x )+ mx dz = 0.

ренциальными уравнениями равновесия прямого бруса.

§ 6.5 ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ РАВНОВЕСИЯ БРУСА

Будем считать, что функции внутренних силовых факторов Nz(z), Qх(z), Qy(z), Mx(z), Mу(z) и Mz(z) в пределах выделенного элементаdz бруса с прямолинейной осью (рис. 2.2) являются полностью дифференцируемыми и интегрируемыми.

Умножим левую и правую части ранее полученного дифференциального

Левая часть равенства (6.8) будет равна: 147

Рассмотрим правую часть равенства (6.8). Геометрической интерпретацией определенного интеграла функции f(z) на участке от a до b (рис. 6.3) является площадь фигуры S, заключенной между осью Oz и кривой f(z). Окончательно получаем:

Отсюда можно сделать следующий вывод: приращение продоль-

ной силы N z в пределах грузового участка равно равнодействующей осевой распределенной нагрузки qz на этом же грузовом участке. Знак

«минус» показывает, что распределенная нагрузка qz , действующая в положительном направлении оси Oz, вызывает отрицательное приращение силы N z .

Рассмотрим дифференциальные уравнения равновесия бруса для плоскости zOy (6.2) и (6.3). После преобразований получаем

Следовательно, приращение поперечной силы Qy в пределах грузового

участка равно равнодействующей поперечной распределенной нагрузки qу на том же грузовом участке. Знак «минус» указывает на то, что

распределенная нагрузка, действующая в положительном направлении оси Oy, создает отрицательное приращение продольной силы Qy .

Рассмотрим частный случай, когда интенсивность распределенного изгибающего момента mx на грузовом участке равна нулю:

Приращение изгибающего момента М х в пределах грузового участка равно площади эпюры поперечных сил Qу на том же грузовом участке.

При перемещении сечения слева направо знак приращения момента М х соответствует знаку суммарной площади эпюры Qу .

148

В общем случае, когда интенсивность распределенного изгибающего момента mx не равна нулю, получаем

Рассмотрим дифференциальные уравнения равновесия бруса для плоскости zOх (6.4) и (6.5). После выполнения преобразований получаем

участка равно равнодействующей поперечной распределенной нагрузки qх на том же грузовом участке. Знак «минус» указывает на то, что распределенная нагрузка, действующая в положительном направлении оси Oх, создает отрицательное приращение поперечной силы Qх .

Рассмотрим частный случай, когда интенсивность распределенного изгибающего момента mу на грузовом участке равна нулю:

участке. При перемещении сечения слева направо знак приращения момента М у соответствует знаку суммарной площади эпюры попереч-

ных сил Qх .

В общем случае, когда интенсивность распределенного изгибающего момента mу не равна нулю, получаем

Рассмотрим последнее, шестое, уравнение равновесия (6.6). После выполнения преобразований получаем

стка равно равнодействующему крутящему моменту от действия распределенных крутящих моментов mz на том же грузовом участке.

Знак «минус» указывает на то, что распределенный крутящий момент,

149