
- |
10 ×(6 - 3)3 |
+ |
4,5×(6 - 5)3 |
- |
4 ×(6 - 5)4 |
= -30,665 кНм3; |
|
|
|
||||
6 |
6 |
24 |
|
|||
v(8 ) = - 30,665 = -11,89 ×10-3 м. 2580
F1=20кН |
|
М1=10кНм |
|
|
|
|
|
|
|
|
|
|
|
М2=20кНм |
|
||||||||||||
|
q=4кН/м |
|
|
|
|
|
|
|
qдогр |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
|
|
|
2 |
3 |
|
|
4 |
|
|
5 |
|
6 |
|
|
|
|
|
|
|
8 |
|
||||
|
z |
||||||||||||||||||||||||||
|
|
A |
|
|
|
|
|
|
|
F2=10кН |
|
|
|
|
|
|
|
|
|
7 qкомп |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
VB=4,5кН |
|
|
|
B |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
VA=30,5кН |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 м |
|
|
||
|
1 м |
|
|
|
|
|
|
|
|
|
2 м |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
2 м |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y
0,0
j0
v0
2,33
 20,0
20,0
10,0 |
Эп. Mх (кН)
3,0
20,0
20,0
11,89
Точка перегиба |
4,97 |
|
|
0,0 |
Эп. v |
0,0 |
(мм) |
1,58 |
|
3,88 |
4,49 |
|
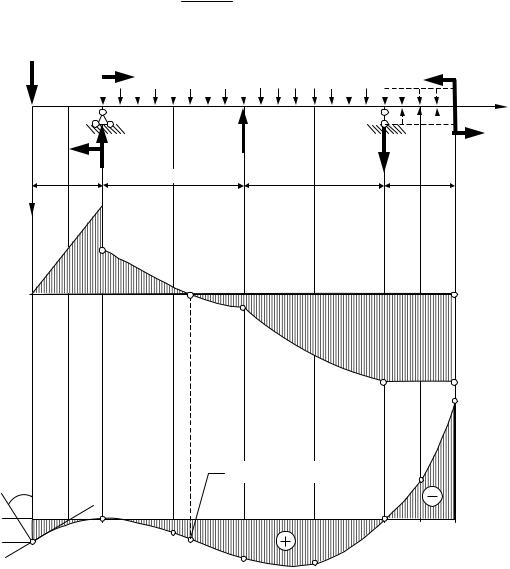
Рисунок 8.7
При построении эпюры прогибов следует помнить, что на участках, где растягиваются нижние волокна балки, эпюра прогибов имеет выпуклость также направленную вниз.
Выполняем проверку жесткости балки. Запишем условие жесткости при поперечном изгибе
[f ]³ vmax .
210
Как следует из эпюры прогибов балки, максимальное вертикальное перемещение равно ½vmax½=1,19 см.
Для стальных конструкций величина допускаемого прогиба определяется из следующего условия: [f ]= l 250 . Здесь l - расстояние между опорами или вылет консоли балки. Максимальный прогиб балки возникает на консольном участке вылетомl =1м. Тогда величина допускаемого прогиба будет равна [f ]= l / 250 =1/ 250 = 4 ×10-3 м=0,4 см.
250 . Здесь l - расстояние между опорами или вылет консоли балки. Максимальный прогиб балки возникает на консольном участке вылетомl =1м. Тогда величина допускаемого прогиба будет равна [f ]= l / 250 =1/ 250 = 4 ×10-3 м=0,4 см.
Условие жесткости балки vmax =1,19 см > [f ]= 0,4 см не выполняется, следовательно, необходимо увеличить размеры поперечного сечения. Назначаем новые размеры двутаврового сечения, для чего максимальный прогиб балки в точке8 приравняем величине допускаемого прогиба:
vmax |
= |
30,665 |
= |
30,665 ×103 |
£ [f ]= 4 ×10-3 м, |
|
EJ x |
2 ×1011 × J x |
|||||
|
|
|
|
тогда требуемый момент инерции поперечного сечения равен:
J x ,nec |
³ |
30,665×103 |
= 3833,12 ×10-8 = 3833,12 см4. |
|
|||
|
2 ×1011 ×4 ×10-3 |
|
|
По сортаменту прокатной стали(ГОСТ8239-89) окончательно принимаем двутавр №27 с J x = 5010 см4.
§8.5 ГРАФОАНАЛИТИЧЕСКИЙ МЕТОД ВЫЧИСЛЕНИЯ ПЕРЕМЕЩЕНИЙ ПРИ ПЛОСКОМ ИЗГИБЕ
Уравнения метода начальных параметров позволяют вычислить углы поворота сечения и прогибы балки в любом сечении балки. При решении целого ряда задач достаточно уметь определять прогиб и угол поворота только в некоторых сечениях. В этих случаях уместно применение графоаналитического метода. Этот метод основан на аналогии между дифференциальными зависимостями при изгибе прямого бруса и дифференциальным уравнением изогнутой оси балки.
Рассмотрим дифференциальную зависимость, связывающую между собой изгибающий момент и интенсивность равномерно распределенной нагрузки
d 2 М х |
= q |
y |
. |
(8.13) |
|
dz2 |
|||||
|
|
|
Сопоставим это уравнение с дифференциальным уравнением изогнутой оси балки
d 2 v(z) |
= |
M x (z) |
. |
||
dz 2 |
|
EJ x |
|
||
211

Между этими двумя уравнениями имеется полная аналогия, по- |
||||||||||||
этому задачу определения прогибов можно свести к определению из- |
||||||||||||
гибающих моментов от некоторой условной(фиктивной) нагрузки в |
||||||||||||
фиктивной балке: |
|
|
|
|
M x (z) |
|
|
|
|
|
||
|
|
|
|
|
q fic = |
. |
|
|
|
(8.14) |
||
|
|
|
|
|
|
EJ x |
|
|
|
|||
Таким образом, при соблюдении некоторых условий, прогиб за- |
||||||||||||
данной балки v |
численно |
равен |
|
фиктивному |
изгибающему |
моменту |
||||||
M fic в фиктивной балке. Учитывая, что |
|
|
|
|
|
|||||||
|
|
|
|
dv |
= j |
|
dM fic |
= Qfic |
, |
|
(8.15) |
|
|
|
|
|
dz |
|
и |
|
|
||||
|
|
|
|
|
|
dz |
|
|
|
|
||
можно сделать вывод, что угол поворота сечения в заданной балкеj |
||||||||||||
численно равен фиктивной поперечной силе Qfic в фиктивной балке. |
||||||||||||
Равенства v = M fic и j = Q fic должны соблюдаться для всех точек |
||||||||||||
двух балок, следовательно, эпюры прогибов и углов поворота должны |
||||||||||||
полностью |
совпадать |
с эпюрами |
|
изгибающих |
моментовM fic |
и попе- |
||||||
речных сил Qfic в фиктивной балке, как по величине, так и по знакам. |
||||||||||||
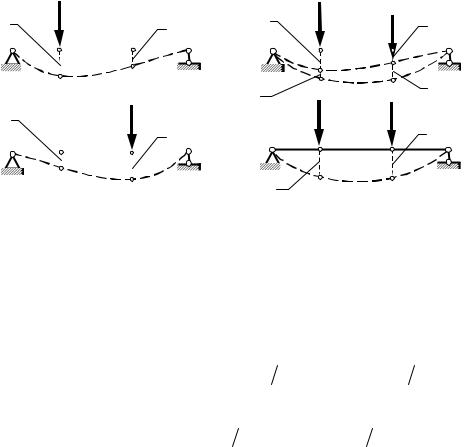
Таблица 8.1 Условия образования фиктивных балок |
|
|
||||||||||
Действительная балка |
vB= 0 |
|
|
Фиктивная балка |
MB= 0 |
|||||||
vА= 0 |
|
|
|
|
MА= 0 |
|
|
|
||||
jА¹ 0 |
|
|
|
|
jB¹ 0 |
QА¹ 0 |
|
|
|
QB¹ 0 |
||
А |
|
|
|
|
B |
|
А |
|
|
|
|
B |
vА= 0 |
|
|
|
vB¹ 0 |
|
MA= 0 |
|
|
MB¹ 0 |
|||
jА=0 |
|
|
|
|
jB¹ 0 QA= 0 |
|
|
QB¹0 |
||||
A |
|
|
|
|
B |
|
A |
|
|
|
|
B |
vА= 0 |
|
|
vB= 0 |
|
vC¹ 0 MА= 0 |
|
|
MB= 0 MC¹ 0 |
||||
jА¹ 0 |
|
|
jB¹ 0 |
|
jC¹ 0 QА¹ 0 |
|
|
QB¹ 0 QC¹ 0 |
||||
А |
|
|
B |
|
C |
|
А |
|
|
|
B |
C |
|
|
|
|
|
|
|
|
|
||||
vD¹0 vА= 0 |
|
vB= 0 |
|
vC¹ 0 |
|
MD¹0 MА= 0 |
MB= 0 |
MC¹ 0 |
||||
jD¹ 0 j ¹ 0 |
|
jB¹ 0 |
|
jC¹ 0 |
|
QD¹ 0 Q |
¹ 0 |
QB¹ 0 |
QC¹ 0 |
|||
А |
|
|
|
|
|
|
|
А |
|
|||
D |
А |
|
B |
|
C |
|
|
D |
А |
|
B |
C |
Для удовлетворения этих равенств необходимо выполнение сле- |
||||||||||||
дующих условий: |
|
|
|
|
|
|
|
|
|
|
|
|
212

-если прогиб заданной балки равен нулю, то в этом же сечении фиктивной балки фиктивный изгибающий момент равен нулю;
-если угол поворота заданной балки равен нулю, то в этом сечении фиктивной балки фиктивная поперечная сила равна нулю;
-если прогиб и угол поворота заданной балки не равны нулю, то соответствующие фиктивные изгибающие моменты и попереч-
ные силы в этом же сечении также не должны равняться нулю. Схемы действительных и соответствующих им фиктивных балок
приведены в таблице 8.1. Следует заметить, что статически определимой действительной балке всегда соответствует статически определимая фиктивная балка. Применение этого метода покажем на следующем примере.
ПРИМЕР 8.5
Исходные данные задачи.
Используя графоаналитический метод построить эпюру прогибов для заданной двухопорной балки (рис. 8.8).
Решение задачи.
Определяем величину опорных реакций заданной балки:
åmВ = 0; VА = 20 + 20 ×3 -10 +10 ×2 = 15 кН;
4
åmА = 0 ; VВ = 20 +10 ×8 -10 - 20 ×3 = 5 кН. 4
Проверка:
å y = 0 ; VA -VB - F1 + F2 = 0 ; 15 - 20 +10 - 5 = 0 .
Используя полученные значения опорных реакций, строим эпюры поперечных сил Q y и изгибающих моментов M x (рис. 8.8).
Выбираем схему фиктивной балки в соответствии с условиями закрепления заданной балки. Фиктивную балку загружаем фиктивной распределенной нагрузкой, изменяющейся по закону изгибающего момента M x в заданной балке. Фиктивную распределенную нагрузку направляем от оси балки в сторону растянутых волокон заданной балки. Ординатами распределенной фиктивной нагрузки являются ординаты ранее построенной эпюры M x , деленные на изгибную жесткости EJ x .
Площадь фиктивной распределенной нагрузки разбиваем на элементарные геометрические фигуры – треугольники и прямоугольники. Действие каждого из элементарных участков фиктивной распределенной нагрузки заменяем равнодействующими wi . Величина равнодейст-
213
вующей wi равняется площади соответствующего элемента фиктивной распределенной нагрузки. Точки приложения равнодействующих находятся в центрах тяжести элементов фиктивной нагрузки. Находим величины равнодействующих wi и координаты точек их приложения ai :
w1 = |
20 |
× 2 = |
40 |
; |
|
|
а = 2 × |
1 |
|
|
|
= 1 м; |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
EJ x |
|
|
|
|
|
|
|
EJ x |
1 |
2 |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
w2 |
= |
|
|
|
20 |
|
|
|
× |
|
3 |
= |
|
|
|
30 |
|
|
|
|
; |
|
а2 |
= 3 × |
|
|
1 |
= 1 м; |
|||||||||||||
EJ x |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
EJ x |
|
3 |
|
|||||||||||||||||||||||||
w3 |
= |
25 |
× |
3 |
= |
|
37,5 |
; |
|
а3 |
= 3× |
2 |
|
|
|
= 2 м; |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
EJ x |
2 |
|
|
|
|
|
|
EJ x |
|
3 |
|
|
|
|||||||||||||||||||||||
w4 |
|
= ( 25 - 10 ) × |
3 |
|
= |
|
22,5 |
; |
а4 |
= 3× |
1 |
|
= 1 м; |
||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
EJ x |
|
|
|
|
|
2 EJ x |
|
3 |
|
|
|||||||||||||||||||||||||
w5 = |
10 |
|
×3 = |
30 |
; |
а = 3× |
1 |
|
=1,5 м; |
||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
EJ x |
|
|
|
|
|
|
|
|
|
EJ x |
5 |
2 |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
w6 |
= |
20 |
× |
2 |
= |
20 |
. |
|
а6 |
= 2 × |
1 |
= 0,67 м. |
|||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
EJ x |
2 |
|
|
|
|
|
|
EJ x |
|
3 |
|
||||||||||||||||||||||||
Для определения опорных реакций фиктивной балки составляем поэтажную схему, позволяющую установить порядок взаимодействия между отдельными элементами многопролетной системы. Построение поэтажной схемы выполняется в следующем порядке: через врезные шарниры мысленно проводят сечения и выявляют элементарные балки, которые могут самостоятельно нести внешнюю нагрузку, без участия остальных элементов. К таким элементам относятся консольные балки и двухопорные балки. Такие балки располагают в нижнем этаже, а ос-
тальные элементы размещают в следующих этажах в соответствии с порядком их примыкания. Балки, не имеющие промежуточных опор, располагаются в самом верхнем этаже поэтажной схемы. Расчет начинаем с балки, расположенной в самом верхнем этаже поэтажной схемы (балка АВ).
Определяем величину опорных реакций фиктивной балки АВ:
åmB = 0; |
VAfic = |
w3 (6 - a3 )+ w4 (3 - a4 )+ w5 (3 - a5 )-w2 (6 - a2 ) |
= |
|
||||||||||||
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
= |
1 |
é37,5×(6 - 2)+ 22,5×(3 -1)+ 30 ×(3 -1,5)- 30 ×(6 -1)ù |
= |
15 |
2 |
|
||||||||||
|
ê |
|
|
|
|
|
|
ú |
|
|
|
кНм |
; |
|||
EJ x |
|
|
6 |
|
|
|
|
|||||||||
|
ë |
|
|
û |
|
EJ x |
|
|||||||||
|
åmА |
= 0 ; |
VBfic = |
w3 a3 + w4 (3 + a4 )+ w5 (3 + a5 )-w2 a2 |
|
= |
|
|
||||||||
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
214

= |
1 |
é37,5 × 2 + 22,5 × (3 +1)+ 30 × (3 +1,5)- 30 ×1ù |
= |
45 |
2 |
. |
||||||||
|
ê |
|
|
6 |
|
|
|
|
ú |
EJ x |
кНм |
|||
|
EJ x ë |
|
|
|
|
|
|
û |
|
|
|
|||
|
|
|
М1=20 кНм |
М2=10 кНм |
F2=10кН |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||||
|
|
C |
A |
|
F1=20кН |
D |
|
|
B |
E |
z |
|
|
|
|
|
y RA=15кН |
|
|
RB=5кН |
|
|
|
|
|
|
|||
|
|
|
3 м |
|
|
2 м |
|
|
|
|
||||
|
|
|
2 м |
|
|
3 м |
|
|
|
|
|
|
||
|
|
|
|
|
5 |
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Эп.Qy |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
(кН) |
|
|
|
|
|
|
20 |
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
25 |
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
Эп.Mx |
|
|
||
|
|
|
|
|
|
|
|
|
|
(кНм) |
|
|
||
|
|
20 |
|
20 |
w4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25 |
w5 |
|
20 |
w |
|
|
|
|
|
|
|
|
|
|
w3 EJx |
|
|
|
|
|
|
|||
|
|
|
|
|
a3 |
|
|
10 |
EJx |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
EJx |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
C |
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
B |
|
E |
|
|
|
|
|
|
|
|
|
|
a4 |
|
|
a6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
20 |
w2 |
a5 |
|
|
|
|
|
|
|
|
|
|
w1 |
|
|
|
|
|
|
|
|
|
|||
|
|
EJx |
EJx |
|
|
|
|
|
|
|
|
|
|
|
|
|
a1 |
|
a2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
Поэтажная схема |
|
B |
|
E |
|
|
|
||
|
|
C |
|
|
D |
|
|
|
|
|
|
|||
|
|
|
|
67,5 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Точка перегиба |
EJx |
|
|
|
|
|
|
|
|
|
|||
|
|
10 |
0 |
|
|
|
|
|
0 |
|
Эп.v |
|
|
|
|
|
EJx |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
Рисунок 8.8 |
|
|
|
116,7 |
|
|
|||
|
|
|
|
|
|
|
|
EJx |
|
|
||||
Используя найденные значения опорных реакций, вычисляем |
||||||||||||||
фиктивный изгибающий момент в сечении D: |
|
|
|
|
|
|||||||||
215

åmD = 0 ; VDfic = w3 (3 - a3 )-w2 (3 - a2 )-VAfic 3 =
37,5 ( ) 30 ( ) 15 67,5 3
= 3 - 2 - 3 -1 - 3 = - кНм ;
EJ x EJ x EJ x EJ x
Знак «минус» указывает, что в точке D растягиваются верхние волокна фиктивной балки. Очевидно, что фиктивные изгибающие моменты в точках А и В равны нулю.
Находим величину опорных реакций фиктивной балкиСА, расположенной в первом этаже поэтажной схемы. Опорные реакции балки АВ, расположенной в верхнем этаже поэтажной схемы, прикладываем к балке СА в противоположном направлении. Тогда:
åmС |
= 0 ; M Cfic = -w1a1 |
+VAfic 2 = |
1 |
(- 40 ×1 +15 × 2)= - |
10 |
кНм3; |
|
EJ x |
EJ x |
||||||
|
|
|
|
|
Определяем величину опорных реакций фиктивной балкиВЕ, расположенной в первом этаже поэтажной схемы. Опорные реакции балки АВ, расположенной в верхнем этаже поэтажной схемы, прикладываем к балке ВЕ в противоположном направлении, получаем:
åmE = 0 ; M Efic = w6 (2 - a6 )+VBfic 2 = ;
= |
1 |
[20 ×(2 - 0,67)+ 45 × 2]= |
116,7 |
кНм3 |
EJ x |
|
|||
|
|
EJ x |
||
По полученным данным строим эпюру фиктивных изгибающих моментов M хfic . Положительные ординаты этой эпюры откладываем в сторону нижних растянутых волокон. В соответствии с графоаналитическим методом определения перемещений при изгибе фиктивный момент M хfic равен прогибу заданной балки v .
Для того, чтобы получить численные значения прогиба v в метрах необходимо задаться материалом, из которого изготовлена балка (определить значение модуля упругости Е) и знать размеры поперечного сечения (вычислить величину осевого момента инерции Jx).
§8.6 ОСНОВНЫЕ ТЕОРЕМЫ ОБ ЛИНЕЙНО-УПРУГИХ ДЕФОРМИРУЕМЫХ СИСТЕМАХ
Действие нагрузки на сооружение вызывает его деформацию. Если нагрузка возрастает достаточно медленно, то такое плавное приложение нагрузки называется статическим. Упругой системой называется система, которая после удаления внешней нагрузки полностью восстанавливает свое начальное недеформированное состояние. Линейно деформируемыми системами называются такие системы, в которых
перемещения и деформации выражаются линейными однородными
216

функциями внешних сил. Например, для
Fсистемы, изображенной на рисунке8.9 получаем
D = aF , |
(8.16) |
где α – коэффициент пропорциональности, зависящий от материала, схемы и размера сооружения.
Увеличим нагрузку F на dF. Это вызовет увеличение перемещения на d . Составим выражение элементарной работыdА, отбрасывая при этом бесконечно малые величины второго порядка малости:
dA = (F + dF )dD = FdD + dFdD » FdD ,
но dD = a × dF , тогда dA = Fa × dF и, следовательно,
F |
F |
aF |
2 |
|
A = òaF × dF =a òFdF = |
|
. |
||
2 |
|
|||
0 |
0 |
|
|
|
Используя формулу (8.16) получаем теорему Клайперона для сосредоточенной нагрузки F:
A = FD 2.
2.
для сосредоточенного момента М:
A = Мj 2.
2.
где j – угол поворота поперечного сечения стержня.
N
dz Dz
а)
γ |
|
M |
|
Q |
Dj |
|
|
|
γ |
y |
|
dz |
D |
dz |
|
||
|
|
|
б) |
|
в) |
Рисунок 8.10 |
|
|
При вычислении работы применяется принцип независимости действия сил. Выразим работу внешних сил через внутренние усилия. Подсчитаем элементарную работу продольных сил N (рис. 8.10а):
dА = |
NDz |
= |
N Ndz |
= |
N 2 dz |
; |
(8.17) |
||
|
|
|
|
|
|||||
N |
2 |
|
2 EA |
|
2EA |
|
|
||
|
|
|
|
|
|||||
работу поперечных сил Q (рис. 8.10б), полагая, что tg γ = |
y/dz » γ, |
||||||||
217

dА = |
QDy |
= |
Q |
gdz = |
Qdz t |
= |
Q dz |
k |
Q |
= k |
Q2 dz |
, |
(8.18) |
||||
|
|
|
|
|
|
|
|
|
|
||||||||
Q |
2 |
|
2 |
|
2 G |
|
2 G |
|
A |
|
2GA |
|
|
||||
|
|
|
|
|
|
|
|
||||||||||
где k – коэффициент, учитывающий неравномерное распределение касательных напряжений τ по поперечному сечению.
Далее подсчитаем элементарную работу изгибающих моментов М
(рис. 8.10в):
dА |
= |
|
MDj |
= |
M Mdz |
= |
|
M 2 dz |
. |
|
|
|
(8.19) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
M |
|
|
|
2 |
|
|
2 |
|
|
EJ |
|
|
|
2EJ |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Суммируя три результата(8.17–8.19), получим значение элемен- |
|||||||||||||||||||||||||
тарной работы от внутренних сил: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
dА = |
|
N 2 dz |
+ k |
Q2 dz |
|
+ |
M 2 dz |
. |
|
|
|
|
(8.20) |
||||||||||||
|
2EA |
2GA |
|
2EJ |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Формула (8.20) для системы, |
состоящей из нескольких элементов, |
||||||||||||||||||||||||
примет вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n l |
N |
2 |
dz |
|
|
n |
l |
2 |
dz |
|
|
n l |
|
|
|
2 |
dz |
|
|
||||||
А = åò |
|
|
+ åòk |
Q |
+ åò |
M |
|
. |
(8.21) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
1 0 |
2EA |
1 |
0 |
|
|
2GA |
|
1 0 2EJ |
|
||||||||||||||||
На основании закона сохранения энергии А = U, где U – потенциальная энергия. Подсчеты показывают, что для системы, работающей на изгиб, первый член формулы (8.21) составляет около 3%, второй – около 1%, третий – порядка 96%.
Рассмотрим систему в состоянии равновесия под действием силы фиксированной величины. Тогда система совершает перемещения, при которых величина и направление внутренних усилий, отвечающих ее исходному состоянию, остаются неизменными, а поэтому их работа будет равна A = FD .
§ 8.7 ТЕОРЕМА О ВЗАИМНОСТИ РАБОТ (ТЕОРЕМА БЕТТИ)
Введем следующее обозначение: mn – перемещение в направлении силы «m» от силы «n». Под перемещением будем понимать смещение и угол поворота, а под силой – силу и момент. Рассмотрим два состояния (рис. 8.11a), для которых
A11 = F1D11 2 , |
|
A22 = F2 D22 2 , |
||||||
или |
|
|
|
|
|
|
|
|
n |
l |
2 |
n |
l |
2 |
n l |
2 |
|
A11 = åò |
M1 dz |
+ åò |
N1 dz |
+ åòk |
Q1 dz |
; |
||
2EJ |
2EA |
|
||||||
1 |
0 |
1 |
0 |
1 0 |
2GA |
|||
218
Состояние I
11 |
|
|
|
F1 |
2 |
21 |
|
11 |
1 |
F1 |
|
F2 |
21 |
|
||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
¢ |
2¢ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1¢ |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
22 |
|
|||||||||
|
Состояние II |
12 |
|
|
|
|
|
2¢ |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
12 |
|
|
|
|
F2 |
|
|
|
|
|
|
1 |
F1 |
|
F2 |
22+ 21 |
||||||
|
1 |
|
22 |
|
|
|
|
|
2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
1¢ |
|
|
|
|
|
|
|
|
|
2¢ |
|
|
|
||||||
|
|
|
|
а) |
|
|
|
11+ 12 |
1¢ |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
Рисунок 8.11 |
|
б) |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
n l |
2 |
|
|
n l |
2 |
|
|
n l |
2 |
|
|
|
|
|||
|
|
|
|
|
|
A22 = åò |
M 2 dz |
+ åò |
N |
2 dz |
+ |
åòk |
Q2 dz |
. |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
1 0 |
2EJ |
1 0 2EA |
1 0 |
|
2GA |
|
|
|
||||||||
|
Далее последовательно приложим к балке сначала силуF1, а за- |
|||||||||||||||||||||
тем силу F2 (рис. 8.11б), тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
A = A11 + A12 + A22 |
= F1D11 |
2 + F1D12 + F2 D22 2 . |
(8.22) |
||||||||||||||
Теперь приложим обе силы одновременно (рис. 8.11б), в этом случае
A = F1 (D11 + D12 ) 2 + F2 (D21 + D22 ) 2 . |
(8.23) |
Приравнивая выражения (8.22) и (8.23), получим теорему о вза-
имности работ (теорему Бетти), которая гласит, что возможная работа внешних или внутренних сил первого состояния на соответствующих перемещениях второго состояния равна возможной работе внешних или внутренних сил второго состояния на соответствующих перемещениях первого состояния, т.е.
F1D12 = F2 D21 |
|
или |
|
A12 = A21 . |
(8.24) |
§ 8.8 ТЕОРЕМА О ВЗАИМНОСТИ ПЕРЕМЕЩЕНИЙ (ТЕОРЕМА МАКСВЕЛЛА)
Рассмотрим два состояния, полученных в результате действия на систему единичных сил (рис. 8.12). На основании теоремы о взаимно-
сти работ (теоремы Бетти) имеем F1d12 = F2d21 . Но, |
учитывая, что |
F1 = F2 =1, получаем d12 = d21 , или в общем виде |
|
dik = dki , |
(8.25) |
219
