2.3. Нормирование погрешностей средств измерений

Нормирование погрешностей средств измерений необходимо для оценивания погрешностей измерения и заключается в установлении предела допускаемой погрешности.

Предел допускаемой погрешности – наибольшая (без учета знака) погрешность средства измерений, при которой оно может быть признано годным и допущено к измерению.

В основе лежат положения:

а) В качестве норм указывают пределы допускаемых погрешностей, включающих в себя систематические и случайные составляющие;

б) Порознь нормируются все свойства средств измерений, влияющие на их точность. Основные и дополнительные. Устанавливаются классы точности изделий.

Класс точности – обобщенная характеристика средства измерения, определяемая пределами, допускаемыми основной и дополнительной погрешностями, а также другими свойствами средств измерений, влияющих на точность.

ГОСТ 8.401-80 – способы нормирования метрологических характеристик. Класс точности выражается числом:

; ;; ; ; ; (где h=1, 0, -1, -2, и т.д.).

Правила и примеры обозначения класса точности средств измерения
Преобладающий вид погрешности	Форма для определения основной погрешности	Пределы допуска при погрешности, %	Обозначение	Пример
Аддитивная ИП	Приведенная		или	1.5 или 2.5
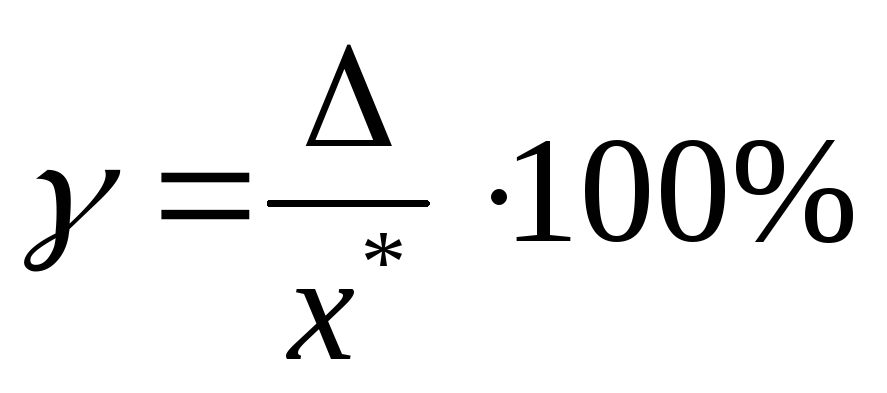
	Относительная			2.5
Аддитивная + мультипликативная ИП	Относительная
			Римские цифры и буквы
Аддитивная ИП	Абсолютные

3. Обработка результатов измерений

3.3. Обработка результатов косвенных измерений

В результате косвенных измерений определяется значение физической величины, функционально связанной с другими физическими величинами, значения которых а₁, а₂, … , а_m.

(3.16)

Пусть каждая величина а_j измерена с погрешностью . Необходимо оценить значение погрешности результата косвенного измерения.

Рассматривая z как функцию m переменных а_j , запишем её полный дифференциал:

или (3.17)

Предположим, что погрешности измерения достаточно малы, заменим в (3.17) дифференциалы соответствующими приращениями:

(3.18)

В (3.18) каждое слагаемое вида представляет собой частотную погрешность результата косвенного измерения, вызванную погрешностьюизмерения величины. Формула (3.18) – приближенная для систематической погрешности.

Если разных знаков, то происходит частичная компенсация их вклада в.

Если заданы предельные значения погрешностей , то можно оценить предельную погрешность:

(3.19)

Если же погрешность независимы, и математические ожидания их равны 0, то математическое ожиданиебудет равно:

(3.20)

а дисперсия:

(3.21)

где - дисперсия погрешностей.

Если проведены серии измерения - прямых:

, …()

всего m – серий по k_j в каждой. То оценка параметра z будет:

(3.22)

где

(3.23)

Причем систематическая погрешность , определяется (3.18), математическое ожидание случайной погрешностиравно нулю, а дисперсия определяется по (3.21).

Важные частные случаи.

1. Функция линейная, т.е., гдес_j – известные коэффициенты. Тогда все:

и формулы приобретают вид:

2. Функция логарифмируема:

- действительные числа.

Прологарифмируем z, а затем возьмем частные производные по :

Здесь удобно рассматривать не абсолютную, а относительную погрешность z:

Пример.

. Пусть ;;;;;.