
- •Вероятностное описание погрешностей измерения
- •1. Случайные события и их вероятности
- •2. Случайные величины и их распределения
- •3. Числовые характеристики случайных величин
- •4. Распределения, часто встречающиеся в задачах метрологии
- •5. Системы случайных величин и их характеристики
- •Введение
- •Научно-техническое
- •Законодательное
- •1.2 Средства измерения и их основные характеристики
- •Средства измерения
- •Измерительные приборы
- •Характеристики средств измерения
- •1.3. Государственная система обеспечения единства измерений
- •Эталоны
- •Электрические измерения
- •2. Погрешности измерений
- •2.1 Классификация
- •Погрешности измерения
- •Методы борьбы с систематическими погрешностями
- •2.3. Нормирование погрешностей средств измерений
- •3. Обработка результатов измерений
- •3.3. Обработка результатов косвенных измерений
- •3.6. Погрешности косвенных измерений
- •Вероятностное описание погрешностей измерения
- •1. Случайные события и их вероятности
- •2. Случайные величины и их распределения
- •3. Числовые характеристики случайных величин
- •4. Распределения, часто встречающиеся в задачах метрологии
- •5. Системы случайных величин и их характеристики
- •1. Необходимые сведения из математической статистики.
- •1.1. Выборка. Статистика.
- •1.2. Оценивание параметров
- •1.3. Несмещенные и состоятельные оценки.
- •1.4. Точность оценивания параметров
- •1. Введение
- •2. Обработка результатов прямых измерений
- •2.1. Точечное оценивание
- •2.2. Оценивание с помощью доверительных интервалов
- •2.3. Примеры решения задач Опыты Милликена [1, стр.102].
- •Проверка статистических гипотез
- •1. Проверка гипотезы о равенстве математического ожидания заданному значению
- •2. Проверка гипотезы о равенстве дисперсии заданному значению
- •3. Проверка гипотезы о равенстве двух дисперсий
- •4. Резко выделяющиеся наблюдения
- •5. Примеры решения задач
- •5.1. Проверка гипотез
- •5.2. Опыты Кэвендиша [1, стр.105]
- •Обработка результатов прямых неравноточных измерений
- •1. Точечное оценивание
- •2. Оценивание с помощью доверительных интервалов
- •3. Пример неравноточных измерений
- •Обработка результатов совместных измерений
- •1. Случай линейной системы уравнений
- •2. Случай нелинейной системы уравнений
- •3. Важные частные случаи
- •3.1. Случай равноточных измерений
- •3.2. Линейная регрессия
- •3.3. Полиномиальная регрессия
- •4. Примеры совместных измерений
- •4.1. Исследование зависимости сопротивления проводника от температуры
- •4.2. Исследование зависимости поверхностного натяжения от потенциала электрода
- •Раздел 4
- •4.1 Основные определения
- •4.1.1 Параметры оптимизации.
- •4.1.2. Факторы.
- •4.1.3 Выбор модели
- •4.2 Пассивные эксперименты.
- •4.3. Активный эксперимент.
- •4.3 Полный факторный эффект.
- •4.3.1 Принцип решения перед планированием.
- •4.3.2 Полный факторный эксперимент типа
- •4.3.3. Понятия о дробной реплике
- •4.2.4 Свойства полного факторного эксперимента.
- •4.3 Крутое восхождение по поверхности отклика.
- •5.2 Активные преобразователи.
- •5.2.1 Пассивные преобразователи.
- •5.2.2 Активные масштабные преобразователи
- •5.3 Измерительные механизмы приборов и их применение.
- •5.3.1Магнитоэлектрические механизмы
- •5.3.2 Электродинамические механизмы
- •5.3.3 Ферродинамические механизмы
- •Компенсаторы
- •4.4.5 Автоматические компенсаторы.
- •4.4.6 Графические самопишущие электроизмерительные приборы (сэп).
- •4.4.6 Светолучевые осциллографы.
- •5.6 Электронные измерительные приборы.
- •Ацпаналогово-цифровой преобразователь.
- •Погрешность квантования
- •6.3. Дискретизация по времени и восстановление непрерывных функций.
- •6.3.1. Теорема Котельникова.
- •6.3.2. Критерии выбора отсчетов и способы восстановления непрерывных функций.
- •6.3.3. Восстановление непрерывных функций интерполяционными полиномами.
- •7.4. Технические характеристики цип.
- •6.5.1. Цифровые фазометры.
- •6.6. Цифровые измерительные приборы для измерения постоянных напряжений и токов.
- •6.6.1. Цифровые вольтметры временного преобразования.
- •6.9. Цип с микропроцессорами.
- •6. Оценивание распределений.
- •6.1. Параметрическое и непараметрическое оценивание.
- •6.2. Гистограмма.
- •6.3. Оценка функции распределения.
- •6.5.2. Цифровые частотомеры (цч)
- •5.6.2 Цифровые вольтметры частотного преобразования
- •5.7 Цифровые измерительные приборы для измерения переменных напряжений и токов.
- •5.8 Цип для измерения параметров электрических цепей
- •5.6.2. Цифровые вольтметры частотного преобразования.
- •Фи – формирователь импульсов стабильной вольтсекундной
2. Случай нелинейной системы уравнений
Для решения нелинейной
задачи осуществляют искусственную
линеаризацию системы нелинейных
уравнений. Пусть задана система нелинейных
уравнений относительно неизвестных
параметров
![]() ,
подлежащих оцениванию:
,
подлежащих оцениванию:
![]()
![]() .
.
При этом предполагается,
что существует некоторое нулевое
приближение
![]() (начальные оценки) неизвестных параметров
(начальные оценки) неизвестных параметров![]() ,
причем погрешность его мала, то есть
разности
,
причем погрешность его мала, то есть
разности![]() малы по сравнению с истинными значениями
оцениваемых коэффициентов
малы по сравнению с истинными значениями
оцениваемых коэффициентов![]()
![]() .
Не рассматривая способа получения
начального приближения
.
Не рассматривая способа получения
начального приближения![]() ,
т.к. в каждом конкретном случае это
является самостоятельной задачей,
остановимся на процедуре уточнения
данного приближения. Про погрешности
,
т.к. в каждом конкретном случае это
является самостоятельной задачей,
остановимся на процедуре уточнения
данного приближения. Про погрешности![]() сделаем те же самые предположения, что
и в линейном случае.
сделаем те же самые предположения, что
и в линейном случае.
Ввиду
малости погрешностей разложим функции
![]()
![]() в
ряд Тейлора в точке
в
ряд Тейлора в точке![]() ,
ограничившись линейными членами:
,
ограничившись линейными членами:
 (11)
(11)
В
системе (11) сначала находятся частные
производные
![]() по
по![]() ,
а затем вычисляются значения этих
частных производных в точке
,
а затем вычисляются значения этих
частных производных в точке![]() .
Получилась система из
.
Получилась система из![]() линейных относительно поправок
линейных относительно поправок![]() уравнений с
уравнений с![]() неизвестными, аналогичная системе (2).
Решая ее по методике, описанной в
предыдущем разделе, находят неизвестные
поправки
неизвестными, аналогичная системе (2).
Решая ее по методике, описанной в
предыдущем разделе, находят неизвестные
поправки![]() и вычисляют первые приближения оценок
и вычисляют первые приближения оценок![]() .
Данную процедуру можно повторить и
найти второе приближение оценок
.
Данную процедуру можно повторить и
найти второе приближение оценок![]() ,
разложив функции
,
разложив функции![]() в ряд Тейлора в точке
в ряд Тейлора в точке![]() и решив получающуюся систему, аналогичную
(11), относительно поправок
и решив получающуюся систему, аналогичную
(11), относительно поправок![]() ,
и т.д. То есть в данном случае оценки
неизвестных коэффициентов
,
и т.д. То есть в данном случае оценки
неизвестных коэффициентов![]() находятся методом последовательных
приближений. Но для успешной сходимости
метода необходимо удачно находить
нулевые приближения
находятся методом последовательных
приближений. Но для успешной сходимости
метода необходимо удачно находить
нулевые приближения![]() ,
что зачастую является очень сложной
задачей.
,
что зачастую является очень сложной
задачей.
3. Важные частные случаи
3.1. Случай равноточных измерений
Постановка
задачи аналогична разделу 1, где
погрешности
![]() измерения величин
измерения величин![]() предполагаются независимыми, нормально
распределенными с нулевым математическим
ожиданием и одинаковой дисперсией
предполагаются независимыми, нормально
распределенными с нулевым математическим
ожиданием и одинаковой дисперсией![]() для всех
для всех![]() ;
то есть измерения равноточные. В этом
случае матрица весов измерений
;
то есть измерения равноточные. В этом
случае матрица весов измерений![]() становится единичной, и выражения для
вектора оценок коэффициентов
становится единичной, и выражения для
вектора оценок коэффициентов![]() (8), оценки дисперсии
(8), оценки дисперсии![]() (9) и матрицы ошибок
(9) и матрицы ошибок![]() (10) несколько упрощаются:
(10) несколько упрощаются:
![]() , (12)
, (12)
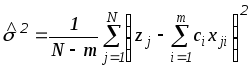 , (13)
, (13)
![]() . (14)
. (14)
При этом все оптимальные свойства оценок (12) сохраняются.
3.2. Линейная регрессия
Очень
часто одна физическая величина
![]() линейно зависит от другой величины
линейно зависит от другой величины![]() (приведите примеры!)
(приведите примеры!)
![]()
где
неизвестные коэффициенты
![]() и
и![]() находят из эксперимента. Для этого при
фиксированных точно известных значениях
находят из эксперимента. Для этого при
фиксированных точно известных значениях![]() :
:
![]() измеряют
соответствующие значения
измеряют
соответствующие значения
![]() ,
но поскольку в измерениях присутствуют
неизбежные ошибки
,
но поскольку в измерениях присутствуют
неизбежные ошибки
![]() ,
то реально результаты измерения
получаются
,
то реально результаты измерения
получаются
![]() ,
где измеренные величины
,
где измеренные величины![]() можно представить в виде
можно представить в виде
![]() .(15)
.(15)
В
такой постановке задача является частным
случаем задачи (2)
из раздела 1, когда относительно
погрешностей
![]() сделаны
те же самые допущения. В этом случае
оценки коэффициентов
сделаны
те же самые допущения. В этом случае
оценки коэффициентов
![]() и
и
![]() получаются
из формулы (8):
получаются
из формулы (8):
![]() , (16)
, (16)
![]() , (17)
, (17)
где обозначено
 ,
,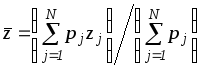 ,
(17а)
,
(17а)
 ,
, .
.
3.3. Полиномиальная регрессия
Согласно теореме
Вейерштрасса [9] любую непрерывную
функцию
![]() можно приблизить на конечном интервале
сколь угодно точно полиномом
можно приблизить на конечном интервале
сколь угодно точно полиномом![]() -го
порядка
-го
порядка
![]() ,
,
выбрав
соответствующие степень полинома
![]() и коэффициенты
и коэффициенты![]() .
.
Поэтому задача
нахождения коэффициентов регрессии
![]()
![]() по измеренным значениям
по измеренным значениям![]() (
(![]() – ошибки измерения) функции
– ошибки измерения) функции![]() ,
выполненных при фиксированных точно
известных значениях
,
выполненных при фиксированных точно
известных значениях![]() независимой переменной
независимой переменной![]() ,
актуальна.
,
актуальна.
Пусть имеется система
из
![]() уравнений относительно
уравнений относительно![]() неизвестных
неизвестных![]()
![]() :
:
![]() ,
,![]() , (18)
, (18)
причем
предполагается, что
![]() ,
а погрешности
,
а погрешности![]() удовлетворяют условиям 1) и 2) раздела
1. Требуется найти оценки неизвестных
коэффициентов
удовлетворяют условиям 1) и 2) раздела
1. Требуется найти оценки неизвестных
коэффициентов![]() из системы
(18).
Т.к. число уравнений больше числа
неизвестных, то данную систему надо
решать по ММП. В этом случае матрица
плана эксперимента имеет вид
из системы
(18).
Т.к. число уравнений больше числа
неизвестных, то данную систему надо
решать по ММП. В этом случае матрица
плана эксперимента имеет вид
 .
.
Введем обозначения
![]()
![]() ,
,
Тогда система (18) примет вид, аналогичный (2)
![]()
![]() . (19)
. (19)
А оценки неизвестных
коэффициентов
![]() ,
параметра
,
параметра![]() и дисперсионной матрицы ошибок
и дисперсионной матрицы ошибок![]() находятся по формулам (8)-(10).
находятся по формулам (8)-(10).
После
нахождения коэффициентов полиномиальной
регрессии необходимо проверить гипотезу
адекватности представления рассматриваемого
явления выбранной моделью. Другими
словами, необходимо ответить на вопрос,
насколько хорошо описывает выбранный
полином
![]() изменение функции
изменение функции![]() в рассматриваемом диапазоне изменения
параметра
в рассматриваемом диапазоне изменения
параметра![]() ;
и если точность описания неудовлетворительна,
то следует увеличить степень полинома
;
и если точность описания неудовлетворительна,
то следует увеличить степень полинома![]() .
.
Статистически
грамотно решить поставленную задачу
можно только в случае, когда известна
дисперсия исходных наблюдений
![]() (или ее можно оценить каким-либо другим
способом, отличным от (9)).
(или ее можно оценить каким-либо другим
способом, отличным от (9)).
Пусть
имеется исходная оценка параметра
![]() ,
которую обозначим
,
которую обозначим![]() .
Тогда для выбора адекватной модели
функции
.
Тогда для выбора адекватной модели
функции![]() (то есть степени
(то есть степени![]() полинома
полинома![]() и соответствующих коэффициентов
регрессии
и соответствующих коэффициентов
регрессии![]() )
в рассматриваемом диапазоне изменения
)
в рассматриваемом диапазоне изменения![]() можно воспользоваться следующей
методикой. Предположим, что априорно
(до опыта) ориентировочно известна
степень полинома
можно воспользоваться следующей
методикой. Предположим, что априорно
(до опыта) ориентировочно известна
степень полинома![]() ,
удовлетворительно описывающая поведение
функции
,
удовлетворительно описывающая поведение
функции![]() в рассматриваемой области (в случае
отсутствия априорных данных лучше всего
начать процедуру подбора степени
полинома с
в рассматриваемой области (в случае
отсутствия априорных данных лучше всего
начать процедуру подбора степени
полинома с![]() ,
то есть
,
то есть![]() ).
Используя наблюдаемые значения
).
Используя наблюдаемые значения![]() ,
находят с помощью (8) оценки коэффициентов
,
находят с помощью (8) оценки коэффициентов![]() и остаточную дисперсию
и остаточную дисперсию![]()
 .
(20)
.
(20)
Далее
составляется
![]() -отношение
-отношение
![]() ,
,
и по критерию
Фишера проверяют (см. часть II, раздел
3), значимо ли отличаются дисперсии
остаточная и исходных наблюдений. Если
отличие незначимое, то с заданной
доверительной вероятностью считают,
что полином
![]() адекватно описывает поведение функции
адекватно описывает поведение функции![]() на заданном интервале. В противном
случае увеличивают степень полинома
на единицу и повторяют процедуру с
полиномом
на заданном интервале. В противном
случае увеличивают степень полинома
на единицу и повторяют процедуру с
полиномом![]() ,и т.д. пока отличие не перестанет быть
значимым. Следует отметить, что вычисление
остаточной дисперсии по формуле (20)
проще, чем по формуле (9), т.к. часть
входящих в (20) сумм была уже подсчитана
при вычислении оценок коэффициентов
регрессии.
,и т.д. пока отличие не перестанет быть
значимым. Следует отметить, что вычисление
остаточной дисперсии по формуле (20)
проще, чем по формуле (9), т.к. часть
входящих в (20) сумм была уже подсчитана
при вычислении оценок коэффициентов
регрессии.
Важно
понимать, что данные методы нахождения
коэффициентов регрессии и проверки
гипотезы адекватности модели можно
применять и в случае, когда вместо
степенных функций
![]()
![]() используются любые другие известные
функции параметра
используются любые другие известные
функции параметра![]() ,
например, гармонические
,
например, гармонические![]() ,
,
![]() и т.д.
и т.д.
