3. Числовые характеристики случайных величин

Законы распределения дают исчерпывающее вероятностное описание любой случайной величины. Однако не всегда удается их получить. Кроме того, в некоторых задачах, в частности при нормировании погрешностей, желательно иметь более компактное описание, ограничивающееся заданием одной или нескольких числовых величин. Такими величинами являются моменты распределений (начальные и центральные).

Начальным моментом k-го порядка называется число

. (3.1)

Центральным моментом k-го порядка называется число

, (3.2)

где – начальный момент первого порядка.

Наиболее часто используемые числовые характеристики распределений случайных величин – математическое ожидание и дисперсия.

Математическим ожиданием случайной величины называется начальный момент первого порядка:

. (3.3)

Такое определение применимо как для непрерывных, так и для дискретных случайных величин. В последнем случае задается соотношением:

. (3.4)

Дисперсией случайной величины называется центральный момент второго порядка:

, (3.5)

где – математическое ожидание, определяемое из (3.3), а–среднеквадратическое отклонениеслучайной величины (СКО).

Для дискретной случайной величины

, (3.6)

а вычисляется из (3.4).

Из (3.5), (3.6) видно, что дисперсия не может быть отрицательной. Она может служить мерой разброса случайной величины относительно математического ожидания. Действительно, если детерминирована и равна, то есть, разброса нет. Тогдаи, а дисперсия из (3.6) равна нулю. Если жеслучайна, и разброс есть, то.

С помощью неравенства Чебышева можно оценить вероятность больших отклонений случайной величины от ее математического ожидания, если известна дисперсия. Для любых

. (3.7)

Известны следующие свойства математического ожидания и дисперсии случайной величины.

, (3.8)

, (3.9)

, (3.10)

где – математическое ожидание случайной величины,,– некоторые константы.

4. Распределения, часто встречающиеся в задачах метрологии

Нормальное распределение. Одним из наиболее часто используемых распределений является нормальное распределение:

. (4.1)

Рис. 2.

Широкое распространение этого распределения обусловлено тем, что в соответствии с центральной предельной теоремой сумма большого числа случайных величин сходится к нормальному распределению независимо от вида распределений этих слагаемых. Погрешности измерения, особенно для прецизионных СИ, вызваны совокупным влиянием большого количества факторов, не поддающихся непосредственному учету. Поэтому предположение о нормальном законе распределения случайных погрешностей измерения во многих случаях оказывается справедливым.

Примерный вид нормальных плотностей вероятностей показан на рис.2. Математическое ожидание случайной величины, распределенной по нормальному закону (4.1), равно , а дисперсия.

На рисунке показаны три кривые для .

Функция распределения нормальной случайной величины имеет вид

, (4.2)

где – табулированный интеграл Лапласа.

Распределение хи-квадрат. Такое распределение имеет сумма квадратов независимых случайных величин с нулевым математическим ожиданием и единичной дисперсией. Число слагаемых называетсячислом степеней свободы. Это распределение используется при построении доверительных интервалов для оценок дисперсий и имеет вид:

, (4.3)

где – гамма функция Эйлера.

Распределение Стьюдента. Такое распределение имеет случайная величина

,

где – распределено нормально с нулевым математическим ожиданием и единичной дисперсией;– имеет распределение хи-квадрат сстепенями свободы. Оно используется при определении доверительных интервалов результатов прямых измерений при экспериментально оцениваемой дисперсии.

(4.3)

Распределение Фишера. Такое распределение имеет величина

,

где величины имеет распределение хи-квадрат сстепенями свободы. Такое распределение используется при анализе оценок дисперсий случайных величин. Оно табулировано для различных значений,.

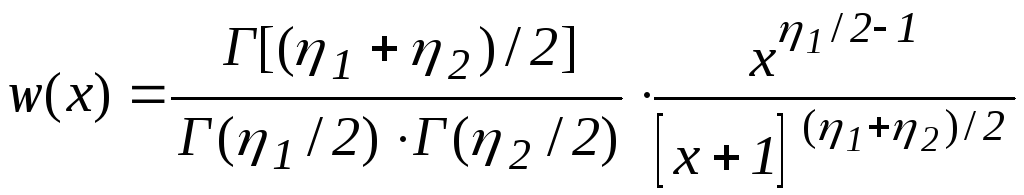. (4.4)