Обработка результатов прямых неравноточных измерений

1. Точечное оценивание

В практике измерений встречаются ситуации, когда оценки измеряемых величин должны быть получены путем обработки результатов измерений, выполненных в различных условиях: различными экспериментаторами, разными методами, с использованием различных средств измерений. При этом часто нет оснований для того, чтобы отдать исключительное предпочтение какой-либо одной группе результатов, а остальные отбросить как не заслуживающие доверия. В то же время степень доверия тем или иным результатам может быть различна, например, из-за различия в точностях примененных средств измерений.

Таким образом, каждому используемому результату или группе результатов измерений необходимо приписать некоторый вес, характеризующий степени доверия этим результатам.

Обычно веса устанавливаются на основе имеющихся данных о степени неопределенности тех или иных результатов, т.е. обратно пропорциональными дисперсиям соответствующих погрешностей результатов измерений:

,

где – вес соответствующий-му результату или-й группе результатов;– дисперсия соответствующих результатов измерений;– неизвестный коэффициент пропорциональности, подлежащий оцениванию наряду с измеряемой величиной.

Рассмотрим задачу обработки результатов прямых неравноточных измерений. Пусть даны результаты неравноточных измерений , которые независимы и имеют нормальное распределение с математическим ожиданиеми дисперсиями, причем весаизвестны. Необходимо найти оценки измеряемой величиныc и параметра .

Плотность распределения любого результата

.

Ввиду этого и в силу независимости наблюдений, функция правдоподобия выборки наблюдений имеет вид

. (1)

Максимум функции правдоподобия достигается при выполнении условия

, (2)

т.е. при выборе по предписанию наименьших квадратов с учетом весов. Приравнивая частную производнуюиз (2) понулю, получаем

. (3)

Оценка называется средней взвешенной оценкой. Несложно показать [1,2], что математическое ожидание и дисперсия оценкисоответственно равны:

;.

Таким образом, оценка является несмещенной, а ее вес равен сумме весов усредняемых результатов. В [1] показано, что данная оценка эффективна.

Для нахождения оценки параметра продифференцируем (1) пои приравняем производную нулю. Из получающегося уравнения вычисляем:

.

Аналогично случаю равноточных измерений вместо используем его оценку максимального правдоподобия (3), тогда:

. (4)

Оценка является смещенной; для ликвидации ее смещенности вводится поправочный множитель

. (5)

2. Оценивание с помощью доверительных интервалов

Построение доверительного интервала для величины основано на том, что величина

распределена по закону Стьюдента с степенями свободы. Поэтому доверительный интервал для истинного значениябудет

, (6)

где – число из таблицы распределения Стьюдента, соответствующее заданному уровню значимостии числу степеней свободы.

Аналогично дробь

,

распределена по закону сстепенями свободы; и доверительным интервалом для параметрабудет

, (7)

где и– числа из таблицы-распределения, соответствующие заданной даверительной вероятности и числу степеней свободы.

3. Пример неравноточных измерений

Двенадцать студентов измеряли сопротивление проводника R одним и тем же способом. Каждый студент провел различное количество наблюдений, подсчитал выборочное среднее значение собственных наблюдений и записал его. Результаты измерений приведены в таблице 1. Считая отдельные наблюдения всех студентов равноточными и независимыми, оценить значение сопротивления проводника и точность его определения, используя результаты измерений выборочного среднего всеми студентами.

Таблица 1.

Номер ст-та j	Среднее значение сопротивления	Число наблюдений	Вес измерения
1	12.208	3	0.231	0.0480	0.009994
2	12.476	4	0.308	0.1466	0.069785
3	12.193	11	0.876	0.1691	0.032630
4	12.306	7	0.538	0.1646	0.050376
5	12.691	6	0.462	0.3192	0.220596
6	12.794	13	1.000	0.7940	0.630436
7	11.660	5	0.385	-0.1309	0.044506
8	12.481	8	0.615	0.2958	0.142287
9	13.363	4	0.308	0.4198	0.572193
10	13.025	9	0.692	0.7093	0.727033
11	12.867	12	0.923	0.8002	0.693809
12	12.717	10	0.769	0.5707	0.395334
		Сумма	7.107	4.3064	3.588979

Если предположить, что отдельные наблюдения у всех студентов не имеют систематических погрешностей, т.е. ошибки измерений распределены по нормальному закону с нулевым математическим ожиданием и неизвестной дисперсией , то подсчитанные ими средние значениябудут уже неравноточными, т.к. студенты провели различное число наблюдений. Поэтому при расчете оценок неизвестных параметровR и выборочные средниедолжны использоваться с учетом весов измерений, которые теория рекомендует выбирать обратно пропорциональными дисперсиям соответствующих погрешностей результатов измерений. В данном случае в качестве весов можно выбрать значения, пропорциональные объему выборокв сериях.

Для удобства расчетов веса отнормированы к значению максимального из , они приведены в таблице в столбце .

В данном случае для решения задачи необходимо воспользоваться результатами раздела 1.1. Оценки неизвестных параметров R и находятся из выражений (3) и (5), но для удобства их вычислений на калькуляторе рекомендуется заменить их на эквивалентные формулы (3а) и (5а), выбрав надлежащим образом величину, например.

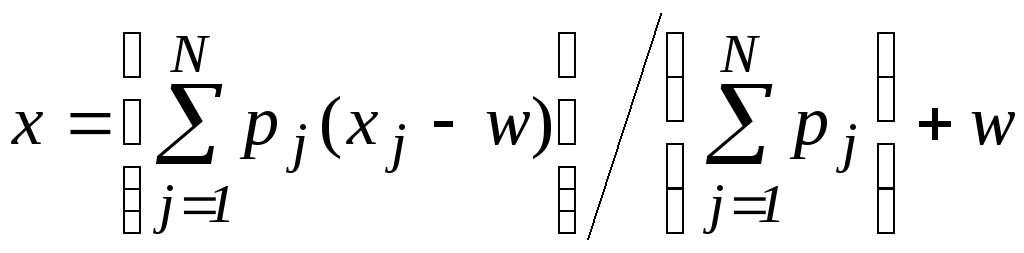(3a)

(5a)

Из (3a) и (5a) находим ; ; .

Теперь построим доверительные интервалы для и. Выберем доверительную вероятность, равной, тогда для числа степеней свободыпо таблице распределения Стьюдента находим. Подставляя значение точечной оценкии величиныв (6), вычисляем . Для тех же самыхипо таблице распределениянаходим два числаии подставляем их в (2) (см. Ч.II). Получаем доверительный интервал для параметра :. Тогда доверительный интервал для равен: .