2. Случайные величины и их распределения

Случайные события характеризуют результаты эксперимента с качественной стороны. Гораздо чаще целью эксперимента является определение размера некоторой физической величины. Именно такие эксперименты составляют предмет любого измерения. По своей физической природе измеряемые величины могут быть детерминированными и случайными.

Будем называть случайной величиной такую величину , которая при выполнении некоторых, заранее оговоренных условий может принимать любое, заранее непредсказуемое значение из некоторого множества значений. Это множество должно содержать не менее двух чисел.

Если величина в ходе эксперимента может принимать только одно значение, то она называется детерминированной.

В зависимости от множества возможных значений случайной величины различают дискретные и непрерывные случайные величины. Если случайная величина может принимать конечное (или счетное) множество значений, то она называется дискретной. Если случайная величина может принимать любое значение из некоторого интервала или совокупности интервалов, то она называется непрерывной.

Дискретные случайные величины полностью характеризуются вероятностями своих отдельных значений:

, .

Для счетного множества . При этом равенствоявляется случайным событием.

Поскольку равенства образуют полную группу событий, то по формуле (1.9) получаем:

. (2.1)

Исчерпывающим вероятностным описанием непрерывной случайной величины является задание законов распределения: функции распределения или плотности вероятности.

Функция распределения определяется следующим образом:

. (2.2)

Текущий аргумент пробегает в общем случае все значения отдо. Можно задать любое конкретноеи по функции распределения определить вероятность того, что произойдет случайное событие, наступление или «ненаступление» которого зависит от заранее неизвестного значения случайной величины.

Из определения вытекают ее свойства:

1) (– невозможное событие);

2) (– достоверное событие);

3) ,– неубывающая функция своего аргумента.

Зная функцию распределения, можно рассчитать вероятность пребывания в интервале. Случайное событиеможно представить в виде суммы несовместных событийи. В соответствии с выражением (1.8) и учетом определения (2.2):

.

Откуда

. (2.3)

Плотность вероятности определяется следующим образом:

. (2.4)

Непосредственно из определений (2.2), (2.4) следует:

;

. (2.5)

В прикладных задачах основное применение находит плотность вероятностей. Учитывая (2.5) и свойства функции , можно получить следующие свойства функции:

1) ;

2) условие нормировки плотности вероятности:

. (2.6)

С учетом (2.3), (2.4) плотность вероятности можно выразить через вероятность пребывания в интервале:

. (2.7)

Использование термина "плотность вероятности" связано с тем, что по аналогии с традиционным определением плотности (например, отношением массы к объему, который она занимает) значение плотности вероятности представляет собой отношение вероятности попадания в заданный интервал к величине этого интервала. Поэтому результаты многократных экспериментов гуще, плотнее расположены в окрестности тех точек, которым соответствует большее значение плотности, и менее плотно в тех точках, гдеменьше.

В случае дискретной случайной величины выражение для плотности вероятности принимает вид

, (2.8)

где – дельта-функция Дирака, определяемая следующими соотношениями и свойствами

;;,

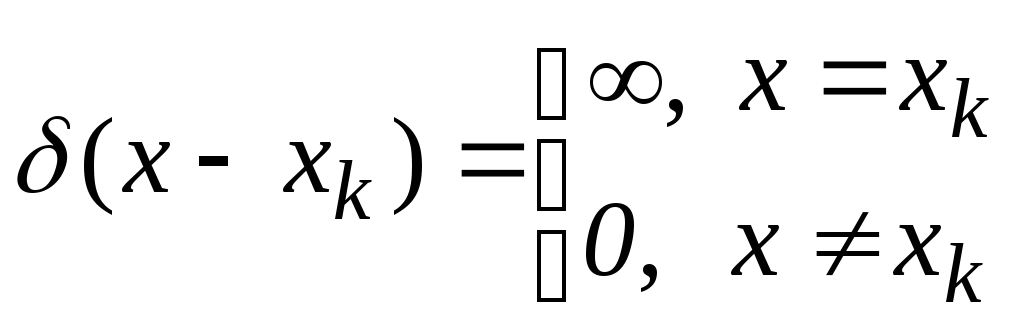– произвольная функция.

Функция распределения, соответствующая плотности вероятностей (2.8), будет иметь ступенчатый вид, а на рис. 1 показаны характерные графики функций ив непрерывном случае.

Рис. 1.