6.3. Дискретизация по времени и восстановление непрерывных функций.

Есть несколько способов дискретизации.

1. Переход от функции непрерывного времени к функции дискретного времени может быть выполнен путем взятия отсчетов функции в определенные дискретные моменты времени 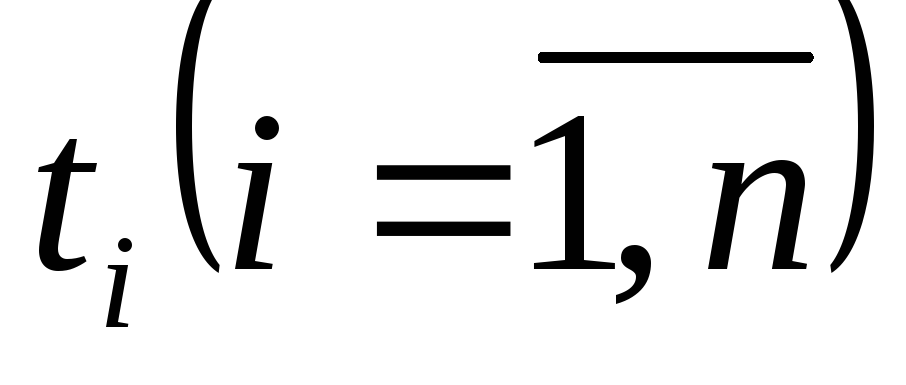. По отсчетамможно восстановить другую функцию (искомую), воспроизводящую исходную с заданной точностью. При дискретизации по времени одним из важнейших является вопрос о выборе шага дискретизации:

.

Существует оптимальный шаг дискретизации, который обеспечивает восстановление исходной функции с заданной точностью при минимальном числе отсчетов на конечном интервале времени.

2. Непрерывная функция на интервале наблюдениязаменяется конечным числом коэффициентов разложенияна выбранной системе базисных функций

Удобство этой системы.

Можно предположить, что точное восстановление исходной непрерывной функции во времени возможно лишь при . Однако существует широкий класс процессов, для которых возможно точное восстановление при конечном значении шага дискретизации. К данному классу относятся сигналы с ограниченным спектром.

6.3.1. Теорема Котельникова.

Если непрерывная функция удовлетворяет условиям Дирихле (ограничена, кусочно-непрерывна и имеет конечное число экстремумов), и ее спектр ограничен некоторой частотой(частота среза), то существует такой минимальный интервалмежду отсчетами, при котором имеется возможность безошибочно восстановить дискретизируемую функциюпо дискретным отсчетам. Этот максимальный интервал:

(6.5)

Основана теорема на возможности разложения функции в ряд:

(6.6)

функция отсчетов (6.7)

Т.е. функцию можно разложить по системе базисных функций. Причем коэффициенты разложениязначенияв дискретные моменты времени.

Свойства :

1. При max значение

2. При

3. Функции ортогональны на бесконечно большом интервале времени.

Практическая ценность разложения функции в ряд Котельникова заключается в том, что каналу связи не передаются известные по виду функции отсчетов , а передаются только решетчатые функции.

С точки зрения практической реализации функция отсчетов полностью соответствует изменению во времени напряжения на выходе идеального фильтра нижних частот, одинаково пропускающего все частоты от 0 до , при подаче на его входимпульса.

В реальных условиях точное восстановление невозможно из-за того, что не выполняются условия теоремы Котельникова.

Реальные функция на конечных интервалах времени, поэтому их спектры бесконечные.

(6.8)

6.3.2. Критерии выбора отсчетов и способы восстановления непрерывных функций.

Если из будет восстановлена функция, то при заданном шаге дискретизации погрешность восстановлениябудет зависеть от способа восстановления, и наоборот, способ восстановления при заданной допустимой погрешности воcстановления будет определять максимальное значение шага дискретизации.

Формулировка задачи: имеется непрерывная функция, требуется определить интервал квантования по времени, при которых отклонение между исходной и восстановленной по ее дискретам функциями не превышало бы заданного значения:

(6.6)

, Т интервал аппроксимации (6.7)

В этом случае решается задача так называемого равномерного приближения функции. Иногда требуют, чтобы в узлах аппроксимации .

Способ восстановления непрерывной функции определяется, прежде всего, видом используемых воспроизводящих функций, которые должны обеспечивать необходимую точность восстановления при минимальном числе членов ряда разложения, а с другой стороны допускать простую техническую реализацию устройств дискретизации и восстановления. В качестве воспроизводящих функций используется ряд Котельникова, ряд Фурье, полином Чебышева, полиномы Лежандра, Хаара, Уолша, степенные полиномы.