2.2. Оценивание с помощью доверительных интервалов

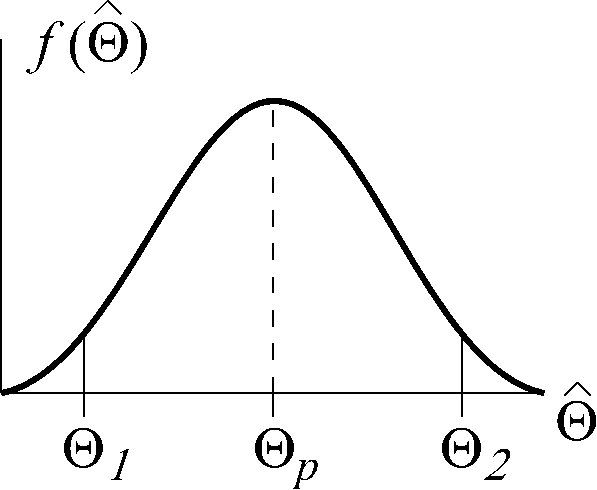
Рис. 2.

Сформулируем сначала общий подход к интервальному оцениванию параметров. Предположим, что необходимо получить доверительный интервал для некоторого параметра , для которого вычислена точечная оценкаи известна плотность распределения этой оценки(рис.2).

Пусть задана доверительная вероятность P. Построить доверительный интервал – это значит найти его границы итакие, что:

.

Чтобы сформулированная задача имела единственное решение, сделаем следующие логически обоснованные допущения:

1. математическое ожидание равно вычисленной точечной оценке;

2. вероятности того, что истинное значение оцениваемого параметра лежит выше верхней границыили ниже нижней границыдоверительного интервала, одинаковы и равны, т.е. границыисимметричны относительнодля симметричных относительно математического ожидания законов распределения.

Определим доверительный интервал для истинного значения с измеряемой величины. Границы этого интервала зависят не только от оценки измеряемой величины, но и от оценкисреднего квадратического отклонения погрешности. Для построения доверительного интервала необходимо вычислить величину [1-3]

. (12)

При нормальном распределении погрешностей величина распределена по закону Стьюдента сстепенями свободы (-распределение). Распределение Стьюдента зависит от числа опытов. В специальных таблицах [1-3] приведены значениядля величины, имеющей распределение Стьюдента сстепенями свободы, определяемые из условия

,

где – плотность-распределения. Полагая(– доверительная вероятность) и зная, по таблице находим границу.

Подставив в (12) значение вместо, получим границы доверительного интервала для измеряемой величины:

. (13)

При построении доверительного интервала для дисперсии случайной погрешности используют случайную величину [1-3]

. (14)

которая при нормальном распределении погрешностей распределена по закону сстепенями свободы. В таблицах [1-3] приведены значениядля величины, имеющей-распределение сстепенями свободы, определяемые из условия

,

где – плотность-распределения. Так как это распределение не симметрично, то по таблице необходимо указать значения верхней и нижней границ интервалаи, соответствующие вероятностями, где– доверительная вероятность. Подставив вместоиз (14) найденные значенияи, получим границы доверительного интервала для дисперсии:

. (15)

2.3. Примеры решения задач Опыты Милликена [1, стр.102].

При определении величины заряда электрона, равной единицCGSE, Милликен получил 58 значений величины (в таблице 1 они обозначены через). На основании проведенных наблюдений требуется оценить истинные значения величины зарядаи дисперсии погрешностей наблюдений.

Точечное оценивание параметров. Оценим сперва истинное значение и дисперсию погрешностей измерения величины . Тогда оценкиидляиполучаются умножением оценок дляна.Оценки дляобозначим соответственнои. Они находятся по формулам (6) и (10) соответственно. Но если вычисления проводятся не на компьютере, а на калькуляторе, то их удобно делать с помощью подходящим образом выбранного числаи очевидных равенств

, (16)

. (17)

В данном случае удобно принять . В таблице приведены значенияи. По формуле (16) имеем. Значит, оценка величины заряда равнаед. Оценка для дисперсии погрешностей измерения величиныполучается по формуле (17):

Таблица 1.

4.781	0.081	0.00656		4.771	0.071	0.00504
4.795	0.095	0.00903		4.809	0.109	0.01188
4.769	0.069	0.00176		4.790	0.090	0.00810
4.792	0.092	0.00846		4.779	0.079	0.00624
4.779	0.079	0.00624		4.788	0.088	0.00774
4.775	0.075	0.00563		4.772	0.072	0.00518
4.772	0.072	0.00518		4.791	0.091	0.00828
4.791	0.091	0.00828		4.788	0.088	0.00774
4.782	0.082	0.00672		4.783	0.083	0.00689
4.767	0.067	0.00449		4.740	0.040	0.00160
4.764	0.064	0.00410		4.775	0.075	0.00563
4.776	0.076	0.00578		4.761	0.061	0.00372
4.771	0.071	0.00504		4.792	0.092	0.00846
4.789	0.089	0.00792		4.758	0.058	0.00336
4.772	0.072	0.00518		4.764	0.064	0.00410
4.789	0.089	0.00792		4.810	0.110	0.01210
4.764	0.064	0.00410		4.799	0.099	0.00980
4.774	0.074	0.00548		4.799	0.099	0.00980
4.778	0.078	0.00608		4.797	0.097	0.00941
4.791	0.091	0.00828		4.790	0.090	0.00810
4.777	0.077	0.00593		4.747	0.047	0.00221
4.765	0.065	0.00423		4.769	0.069	0.00476
4.785	0.085	0.00723		4.806	0.100	0.01124
4.805	0.105	0.01103		4.779	0.079	0.00624
4.768	0.068	0.00462		4.785	0.085	0.00723
4.801	0.101	0.01020		4.790	0.090	0.00810
4.785	0.085	0.00723		4.777	0.077	0.00593
4.783	0.083	0.00689		4.749	0.049	0.00240
4.808	0.108	0.01166		4.781	0.081	0.00656
				Сумма	4.687	0.39209

; тогда, а оценкой длябудетед.

Оценивание параметров с помощью доверительных интервалов. Найдем интервал, про который можно сказать, что он с доверительной вероятностью накрывает оцениваемые значения параметрови. Возьмем. По таблице распределения Стьюдента для заданныхи числа степеней свободынаходим. По формуле (13) вычисляем искомый доверительный интервал. Для той же самой доверительной вероятностипо таблице распределениясстепенями свободы находим два числаии подставляем их в (15). Получаем доверительный интервал для параметра:. Откуда вычисляем доверительный интервал для:.