5. Системы случайных величин и их характеристики

С системами случайных величин сталкиваются во всех случаях, когда результаты эксперимента характеризуются несколькими случайными величинами, которые в силу взаимной зависимости необходимо рассматривать как единое целое, например, как случайный вектор , где знакобозначает операцию транспонирования матрицы. С системами случайных величин имеют дело при обработке результатов косвенных, совокупных и совместных измерений.

Способы описания системы случайных величин аналогичны способам описания одномерных случайных величин. Исчерпывающими вероятностными характеристиками системы из случайных величин является-мерная функция распределения

(5.1)

или -мерная плотность вероятности

. (5.2)

Как и в случае одномерном, многомерные функции распределения и плотности вероятности взаимнооднозначно определяют друг друга:

,

. (5.3)

Многомерная функция распределения удовлетворяет следующим условиям:

1) ;

2) ;,

3.  , .

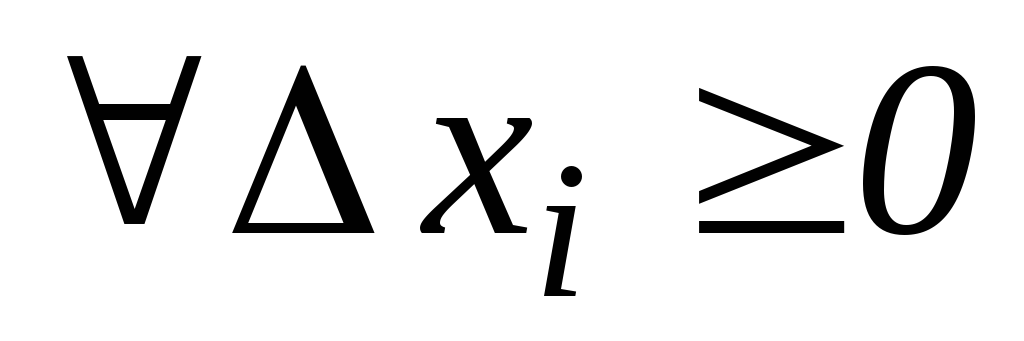Свойства многомерной плотности вероятностей аналогичны свойствам одномерной:

1) ;

2) . (5.4)

Аналогично (2.7) определяется вероятность пребывания случайного вектора в любой области-мерного пространства:

. (5.5)

Если координаты случайного вектора статистически независимы, то

. (5.6)

Это соотношение является необходимым и достаточным условием для статистической независимости случайных величин.

Математическим ожиданием функции нескольких случайных величин называется число

. (5.7)

Для -мерного случайного векторатакже вводятся понятия математических ожиданий его компонент и вторых центральных моментов:

, ,(5.8)

. (5.9)

Очевидно, что . Матрица, компоненты которой являются случайными величинами, называетсяслучайной матрицей. Математическим ожиданием случайной матрицыназывается матрица, компоненты которой равны математическим ожиданиям компонент матрицы.

Симметрическая матрица , компонентами которой являются величиныиз (5.9), называетсяковариационной матрицей случайного вектора . В матричном виде выражение для нее будет:

. (5.10)

Для независимых случайных величин справедливы следующие важные свойства:

, (5.11)

. (5.12)

В приложениях метода наименьших квадратов часто приходится иметь дело с -мерным случайным вектором, компоненты которого распределены по нормальному закону и представляют собой случайные погрешности наблюдения. При этом зачастую составляются линейные комбинации наблюдений и их погрешностей вида:

, (5.13)

где – случайный вектор, получающийся из векторапутем линейного преобразования, задаваемого матрицейразмера. Еслии ранг матрицыравен, то векторбудет называться невырожденным, и его компоненты тоже будут распределены нормально. Причем вектор математических ожиданий:

, (5.14)

а ковариационная матрица :

. (5.15)

Для двух случайных величин и, имеющих совместное распределениемерой их статистической зависимости являетсякоэффициент корреляции:

, (5.16)

где – второй центральный момент распределения, задаваемый выражением (5.9). Если, то величиныистатистически независимы, и наоборот, если, то междуисуществует линейная зависимость.

1. Необходимые сведения из математической статистики.

1.1. Выборка. Статистика.

Основным понятием математической статистики является выборка или совокупность, наблюдений какого-либо количественного показателя. Ее еще называют выборка из генеральной совокупности. Допустим, что имеется n значений некоторой величины, которые объединены в один вектор , где^T обозначает операцию транспонирования матрицы. Число n называется объемом выборки. Также полагается, что наблюдения данной величины получены в результате измерений, сопровождавшихся неизбежными случайными ошибками, поэтому величины x_i все различны. Совокупность всех величин x_i называется случайной выборкой, которую удобно рассматривать как n-мерный случайный вектор. Если предположить, что было произведено бесконечное количество опытов, в которых измеряемая величина приняла некоторые значения x_i (n = ), то совокупность всех этих значений есть генеральная совокупность.

Выборка называется повторной, если все x_i независимы и имеют одинаковый закон распределения F₁(x):

в противном случае выборка бесповторная.

Любая функция от величин x_i называетсястатистикой. В общем случае она может быть дискретной или непрерывной, но в дальнейшем будут рассматриваться только непрерывные статистики.

Примеры статистик:

– выборочное среднее,

– выборочная дисперсия,

– наибольший элемент выборки.