
Osnovy_teploperedachi_i_massoobmena_2015
.pdf
тем диффузии свободных электронов и имеет место тогда, когда в различных точках тела температура не одинакова.
1.2. Основной закон теплопроводности. Закон Фурье
Перенос теплоты теплопроводностью (который в чистом виде имеет место только в твердых телах с малым коэффициентом термического расширения) выражается эмпирическим законом Био–Фурье:
(1.5)
Количество теплоты dQ, проходящее через элемент изотермической поверхности dF (м²) за промежуток времени dτ, пропорционально градиенту температуры ∂t/∂n. Коэффициент пропорциональности λ (коэффициент теплопроводности) – это справочная характеристика, его значение различно для различных материалов, характеризует способность тел проводить теплоту.
Градиент температуры ∆n – это наикратчайшее расстояние
между соседними изотермами, тогда lim |
t |
= |
t |
, К/м, который назы- |
|
n |
n |
||||
n 0 |
|
|
вается градиентом температуры grad t. Градиент температуры характеризует интенсивность возрастания температуры по нормали к изо-
термической поверхности. nt – векторная производная, положитель-
ное направление которой указывает в сторону возрастания температуры. Часто требуется подсчитать изменение температуры в произвольном направлении, например в направлении оси x:
Рис. 1.1
- 13 -

grad t |
|
t |
cos(n,x ) |
t |
; cos(n,x ) |
n |
|
n |
. |
|
n |
x |
x |
|
|||||
|
x |
|
|
|
x |
||||
Коэффициент теплопроводности λ характеризует способность тел проводить теплоту, его величина характеризует количество теплоты, которое проходит в единицу времени через единицу площади поверхности при температурном grad = 1. Коэффициент теплопроводности, как правило, определяется опытным путем и зависит от температуры и давления:
= |
|q | |
, Вт/(м·К). |
(1.6) |
||
grad t |
|||||
|
|
|
|
||
|
|
|
|
Таблица. 1.1 |
|
Ориентировочные значения λ различных веществ при t=20 °C |
|||||
|
|
|
|
|
|
Вещество |
|
|
|
λ,Вт/(м·К) |
|
Воздух |
|
|
|
0,025 |
|
Вода |
|
|
|
0,6 |
|
Твердые материалы |
|
||||
Асбест |
|
|
|
0,11 – 0,3 |
|
Кирпич |
|
|
|
0,8 |
|
Пенопласт |
|
|
|
0,05 |
|
Стекловата |
|
|
|
0,047 |
|
|
Металлы |
|
|||
Углеродистая сталь |
|
|
|
45 – 60 |
|
Медь |
|
|
|
390 |
|
Количество теплоты, проходящее через единицу площади поверхности в единицу времени, называют плотностью теплового потока:
(1.7)
Плотность теплового потока есть вектор, положительное направление которого указывает в сторону уменьшения температуры (рис. 1.1). Тогда основной закон теплопроводности может быть записан в виде
(1.8)
- 14 -
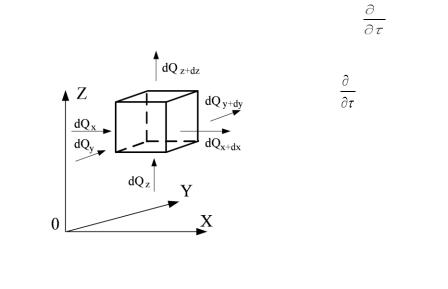
Направления grad t и q противоположны, этим объясняется знак «–» в законе Фурье.
Для подсчета q в любой точке тела необходимо знать значение grad t = ∂t/∂n. Температурное поле внутри тела может быть определено в общем случае для конкретной задачи лишь путем решения дифференциального уравнения теплопроводности.
1.3. Дифференциальное уравнение теплопроводности
Для упрощения вывода сделаем следующие допущения: будем считать, что тело однородно и изотропно. Его физические параметры, например λ= const, СP = const, ρ = const, не зависят от температуры. Пренебрежем также деформацией объема вследствие переноса теплоты, так как она мала по сравнению с самим объемом. Вывод дифференциального уравнения теплопроводности основан на применении закона сохранения энергии, который применительно к данному случаю может быть сформулирован следующим образом: количество теплоты dQ, введенное в элементарный объем dV за промежуток времени dτ, вследствие теплопроводности идет на изменение внутренней энергии вещества dU, содержащегося в данном объеме:
dQ =dU=ρCV t dVdτ ,кДж, (1.9)
где ρ – плотность, кг/м³; CV, – теплоемкость при постоянном объеме,
кДж/(кг·К); t , К/с; dV, м³; τ, с.
Выделим в теле элементарный объем (рис.1.2). Обозначим через dQx, dQy и dQz количества теплоты, которые подводятся к граням элементарного объема в направлении осей 0X, 0Y, 0Z. Обозначим также
через dQx+dx, dQy+dy и dQz+dz количества теплоты, которые отводятся от противоположных граней элементар-
Рис. 1.2 ного объема в направлении тех же осей.
- 15 -

Подсчитаем dQx = qxdydzdτ (dydz = dF), где qx – проекция вектора плотности теплового потока на ось 0X:
dQx+dx = qx+dxdydzdτ.
Подсчитаем избыток теплоты в направлении оси 0X и всех остальных осей:
dQx– dQx+dx = (qx– qx+dx) dydzdτ = …
Для получения этого избытка теплоты функцию (qx+dx) разложим в ряд Тейлора с точностью до второго члена ряда:
qx+dx= qx+ |
qx |
dx+… |
|
x |
|||
|
|
и подставим значение функции
dQx dQx dx = qx |
qx |
qx |
|
x |
|||
|
|
где dxdydz = dV.
По аналогии
qx+dx в избыток теплоты. Получим
dx dydzd |
qx |
dVd , |
|
x |
|||
|
|
dQ |
|
dQ |
|
qy |
dVd ;dQ |
|
dQ |
|
qz |
dVd . |
y |
y dy |
|
z |
z dz |
z |
|||||
|
|
y |
|
|
||||||
|
|
|
|
|
|
|
|
|||
Согласно закону сохранения энергии этот избыток Q идет на изменение внутренней энергии вещества, содержащегося в данном объеме:
dQ |
|
|
q |
x |
|
|
qy |
|
|
q |
z |
|
dVd |
|
C |
|
|
t |
dVd . |
|
|
|||||||||||||
|
|
x |
|
|
|
y |
|
z |
|
v |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
t |
1 |
|
|
|
|
q |
x |
|
|
|
qy |
|
|
|
|
q |
z |
. |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
Cv |
|
|
|
|
x |
|
y |
|
|
|
|
z |
|
|
|
|
|
|
|
|
||||||||
По закону Фурье |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
qx qn |
|
cos(n,X ) |
|
|
|
t |
|
cosn,X ; |
t |
cos(n,X ) |
t |
. |
||||||||||||||||||||||
|
|
|
n |
|
n |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|||||
|
qx |
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
2t |
, |
|
|
|
|
|
|
|
|||
|
x |
|
|
x |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
x 2 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- 16 - |
|
|
|
|
|
|
|
|
|
|||||
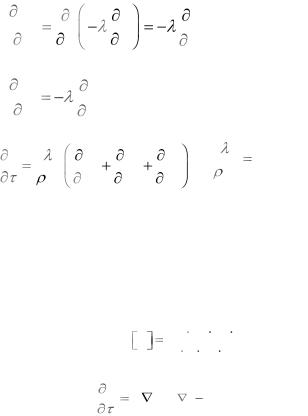
|
qy |
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
2t |
, |
|
|
|||
|
|
y |
|
|
y |
|
|
|
|
|
y |
|
|
|
|
|
y 2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
qz |
|
|
|
|
|
2t |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
z 2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
t |
|
|
|
|
|
|
|
2t |
|
|
2t |
|
2t |
|
, |
|
|
|
a , |
|||||
|
|
|
|
|
|
|
C |
|
||||||||||||||||
|
|
|
|
Сv |
x |
2 |
|
|
|
y |
2 |
|
z |
2 |
|
|
v |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где a – физический параметр вещества, характеризующий скорость изменения температуры в нестационарных процессах, который был назван коэффициентом температуропроводности. Это мера теплоинерционных свойств тела. Чем больше значение а, тем больше скорость изменения температуры в теле и тем меньше тепловая инерционность тела. Наивысшее значение для а характерно для металлов. Размерность коэффициента температуропроводности:
аВт м3 кг К=м2 ,
мК кг Дж с
тогда
t |
а |
2t , |
2 оператор Лапласа. |
|
|
(1.10) |
|||
|
|
|
|
Дифференциальное уравнение теплопроводности устанавливает связь между пространственным и временным изменением температуры. Рассмотрим применение дифференциального уравнения теплопроводности для решения некоторых практических задач теплопроводности.
- 17 -
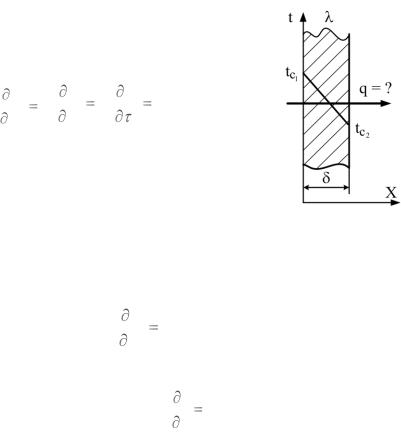
1.4. Применение дифференциального уравнения теплопроводности для решения практических задач 1.4.1. Теплопроводность плоской однослойной стенки при стационарном режиме
Сформулируем задачу. При этом будем считать, что два размера стенки, например, в направлении осей Y и Z являются существенно бóльшими по сравнению с ее толщиной (рис. 1.3), и поэтому
|
2t |
0; |
2t |
0; |
t |
0. |
|
|
|
z 2 |
|
|
|||
|
у 2 |
|
|||||
Тогда |
|
|
|
|
|
|
|
|
|
t=f(x). |
|
|
(1.11) |
||
При стационарном режиме на поверхностях стенки установились во времени тем-
пературы tc1 и tc2.
Для получение формулы для плотности теплового потока необходимо решить дифференциальное уравнение теплопроводности для сформулированной нами
задачи, чтобы получить закон изменения температуры в данной стен-
ке. Поскольку t=f(X), то |
2t |
0 |
– и мы имеем дифференциальное |
||
x |
2 |
||||
|
|
|
|||
уравнение теплопроводности для стационарной одномерной задачи. Первое интегрирование дает
t |
C |
|
. |
|
1 |
||
x |
|
||
|
|
||
Второе интегрирование дает закон изменения температуры в такой стенке: t = C1X+C2. Это уравнение прямой. Значит, в плоской стенке температура меняется по линейному закону и не зависит от свойств материала.
Запишем граничные условия:
1. X=0, t=tc1=C2;
- 18 -
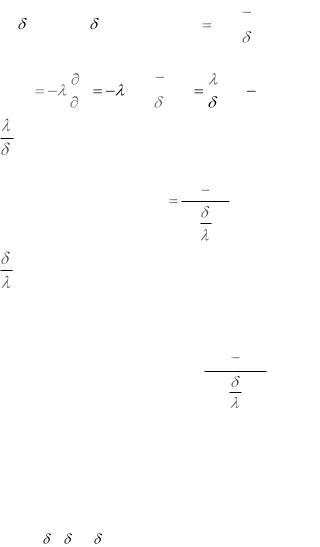
2. X= ,t=tc2=C1∙ +tс1.Отсюда С |
|
|
|
tc 2 |
tc 1 |
. |
|
|
|
|||||
1 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Запишем закон Фурье: |
|
|
|
|
|
|
|
|
|
|
|
|||
q |
t |
|
tc 2 tc 1 |
|
|
|
t |
|
t |
|
|
, |
Вт |
, |
x |
|
|
|
|
|
c 1 |
c 2 |
м2 |
||||||
|
|
|
|
|
|
|
|
|
|
|||||
где – тепловая проводимость плоской однослойной стенки. Отсюда
плотность теплового потока:
q tc 1 tc 2 ,
где – термическое сопротивление теплопроводности плоской одно-
слойной стенки.
Если известна площадь поверхности, через которую передается теплота, то
Q = qF= tc 1 tc 2 , Вт.
Тепловой поток пропорционален температурному напору на поверхности плоской стенки tc1 – tc2 и обратно пропорционален термическому сопротивлению.
1.4.2. Теплопроводность плоской многослойной стенки
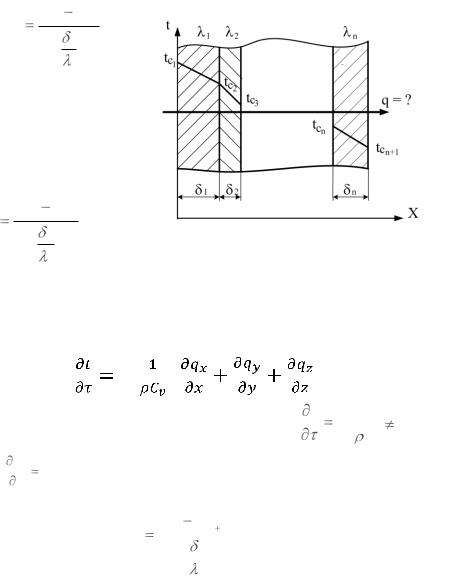
Допустим, что плоская стенка состоит из n разнородных слоев толщиной 1, 2… n с коэффициентами теплопроводности λ1, λ2…. λn (рис. 1.4). Слои такой стенки плотно прилегают друг к другу, поэтому температура на соприкасающихся поверхностях одна и та же.
При стационарном режиме в стенке установились во времени температуры tc1,tc2,tc3,tcn,tc(n+1). Тогда для первого слоя
- 19 -
q tc 1 tc 2 .
1
1
При стационарном режиме численно то же значение плотности теплового потока для второго слоя:
q tc 2 tc 3 .
2 |
|
2 |
Рис. 1.4 |
|
Докажем, что это так.
Для этого используем промежуточное выражение дифференциального уравнения теплопроводности
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.12) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
||||
Это объясняется тем, что при стационарном режиме |
0, |
1 |
0. |
||||||||||||||||||||
|
|
||||||||||||||||||||||
|
|
Сv |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Тогда |
qx |
0 , qx = const.Для n-го слоя значение плотности теплового |
|||||||||||||||||||||
x |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
потока составит |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
q |
tcn tc (n 1) |
. |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
||||||
n
Записанные исходные соотношения переписываем каждое относительно температурного напора и складываем:
- 20 -

tc 1 tc (n 1) |
q |
|
1 |
|
|
|
2 |
|
..... |
n . |
||||
|
|
|
|
1 |
|
|
|
2 |
|
|
|
n |
|
|
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
tc 1 tc (n 1) |
|
, |
Вт |
. |
|
|
||||||
|
|
n |
|
м2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
i 1 i
Последнее соотношение может быть переписано в виде
(1.13)
Заметим, что знаменатель представляет собой сумму термических сопротивлений многослойной плоской стенки. Его величина не меняется от перестановки слоев многослойной стенки, и поэтому не изменяется плотность теплового потока и сам тепловой поток.
1.4.3. Теплопроводность однослойной цилиндрической стенки
Задача решается в цилиндрических координатах (рис. 1.6). При этом уравнение температурного поля в общем виде запишется:
t=f (τ,r,φ,z) |
(1.14) |
Переход от полярных (рис. 1.5) к цилиндрическим координатам приводит к дифференциальному уравнению теплопроводности в общем виде
|
|
|
=a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Сформулируем |
|
задачу. |
||||||||||||||
Рис. 1.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2t |
|
||||
Пусть l >> r2 |
– r1, тогда |
z |
2 0. |
||||||||||||||||
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
- 21 -
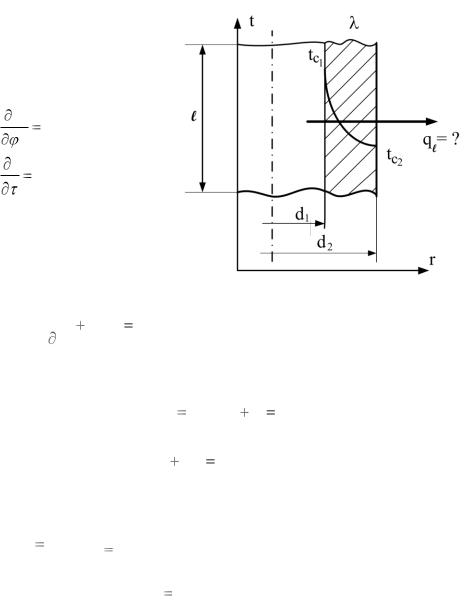
Будем считать, что температура в цилиндрической стенке не меняется по окружности цилиндра, поэтому
2t
2 0 , а также
t
0 (так как ста-
ционарный режим). Тогда дифференциальное уравнение для сформулированной нами задачи запишется в виде
d 2t |
1 dt |
0. |
|
|
|
Рис. 1.6 |
|
r 2 |
r dr |
|
|
|
|
|
|
Введем новую переменную u: |
|
|
|||||
|
|
|
dt |
u , |
du |
u |
0. |
|
|
|
dr |
|
dr |
r |
|
Разделим переменные: |
du |
dr |
0 |
|
|
||
|
|
|
u |
r |
|
|
|
и проинтегрируем: lnu+lnr = const = С1. Перепишем последнее выражение в виде u∙r = С1'. Подставим значение u:
dt |
r |
С1 |
', dt |
C1 ' |
. |
|
dr |
|
|
||||
|
|
dr |
r |
|
||
|
|
|
|
|
|
dr |
Разделим переменные: dt С1 ' |
r . |
|||||
Проинтегрируем:
t=С1'∙lnr + С2.
- 22 -
