Казанский национальный исследовательский технологический университет

Отчет по дисциплине вычислительная математика

Выполнила работу:

студентка 1 курса

группа 61-21-21

Манина Юлия

Проверила:

доцент Кошкина Л. Ю.

Казань 2013

Оглавление

Тема 1. Численное решение алгебраических и трансцендентных уравнений 2 Тема 1. Численное решение алгебраических и трансцендентных уравнений

Постановка задачи:

Дана функция f(x)= x ^ 3 - 2 * x ^ 2 - 4 * x + 7, равная 0, которая определена и непрерывна на интервале [a;b]. Найти x с заданной точностью Е=0,0001.

Решение:

1. Отделение корней

x=	f(x)
-5	-148
-4	-73
-3	-26
-2	-1
-1	8
0	7
1	2

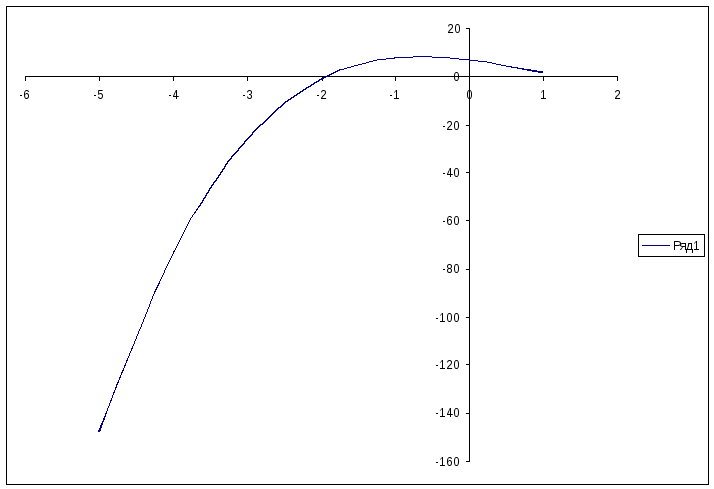
2. Уточнение корней методами половинного деления, касательных, хорд, простой итерации

Function f(x)

f = x ^ 3 - 2 * x ^ 2 - 4 * x + 7

End Function

Sub Метод_пол_деления()

a = -2

b = -1

e = 0.0001

n = 0

Do

x = (a + b) / 2

F1 = f(a)

F2 = f(b)

If F1 * F2 > 0 Then

a = x

Else

b = x

End If

n = n + 1

Loop While Abs(b - a) >= e

With Worksheets("Лист3")

.Range("E2").Value = x

.Range("F2").Value = n

.Range("G2").Value = f(x)

End With

End Sub

Sub Метод_касательных()

x = -2

e = 0.0001

n = 0

Do

x1 = x - f(x) / (3 * x ^ 2 - 4 * x - 4)

c = Abs(x1 - x)

x = x1

n = n + 1

Loop While c >= e

With Worksheets("Лист3")

.Range("E3").Value = x

.Range("F3").Value = n

.Range("G3").Value = f(x)

End With

End Sub

Sub Метод_хорд()

x = -2

e = 0.0001

n = 0

p = -1

Do

x1 = x - f(x) / (f(x) - f(p)) * (x - p)

c = Abs(x1 - x)

x = x1

n = n + 1

Loop While c >= e

With Worksheets("Лист3")

.Range("E4").Value = x

.Range("F4").Value = n

.Range("G4").Value = f(x)

End With

End Sub

Sub Метод_простой_итерации()

e = 0.0001

n = 0

x = -1

Do

x1 = (x ^ 3 - 2 * x ^ 2 + 7) / 4

c = Abs(x1 - x)

x = x1

n = n + 1

Loop While c >= e

With Worksheets("Лист3")

.Range("E5").Value = x

.Range("F5").Value = n

.Range("G5").Value = f(x)

End With

End Sub

Результаты:

метод	x=	n=	f(x)=
полов.дел.	-1,93756	14	-0,03192
касат.	-1,93543	3	-3,9E-11
хорд	-1,93547	26	-0,00056
прост.ит.	-1,93675	7	-8,8E-06

Вывод:

Если рассматривать сложность методов, то все они достаточно просты. Здесь можно выделить метод половинного деления, который всегда сходится, если на рассматриваемом интервале [a;b] есть корень, но число итераций у него наибольшее. Время решения уравнений зависит от числа итераций и времени, затрачиваемом на одну итерацию. Время итераций зависит от того, сколько раз вычисляется функция и производная. Так в методе касательных помимо функции рассчитывается еще и производная. В случае, если производная равна нулю, то решение этим методом невозможно. Если сравнивать методы по числу итераций, все зависит от вида функции. Как правило, наименьшее число итераций в методе касательных. Для метода простой итерации необходимо строгое выполнение условия сходимости.

Для уравнения x ^ 3 - 2 * x ^ 2 - 4 * x + 7=0 на интервале [-2;-1] самым простым является метод касательных, так как используется небольшое количество итераций и найденное значение имеет наименьшую погрешность.