
Osnovy_teploperedachi_i_massoobmena_2015
.pdf
и дифференциальное уравнение энергии для пограничного слоя запишется:
Дифференциальное уравнение вынужденного движения при наличии свободного движения. Для проекций сил на ось 0X 

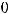
(так как процесс стационарный). Принимая во внимание, что поток безграничен в направлении оси 0Z
Учитывая, что для гидродинамического пограничного слоя 
 l, то
l, то

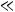
 , и отсюда
, и отсюда 


 Для пограничного слоя
Для пограничного слоя 

 . Тогда
. Тогда
(2.7)
где 

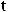 – объемная подъемная сила, возникающая в жидкости при наличии в ней разности температур. Размерность этой силы составит:
– объемная подъемная сила, возникающая в жидкости при наличии в ней разности температур. Размерность этой силы составит:
Оценка порядка членов дифференциального уравнения движения для проекций сил на ось Y позволяет сделать вывод, что эти члены существенно меньше соответствующих членов дифференциального уравнения движения для проекций сил на ось X, поэтому для пограничного слоя дифференциальное уравнение движения для проекций сил на ось Y можно опустить.
Дифференциальное уравнение теплоотдачи
(2.8)
- 73 -
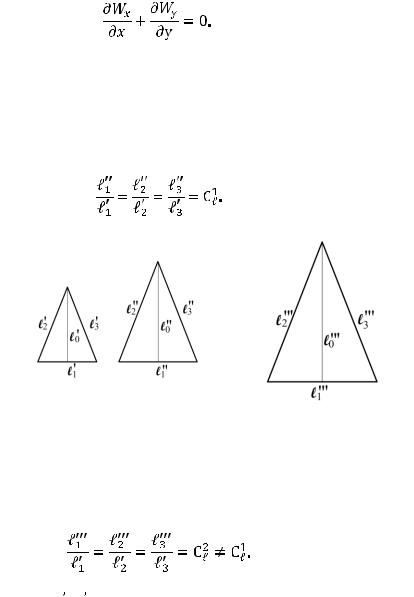
Дифференциальное уравнение неразрывности
(2.9)
2.3. Теория подобия
Термин «подобие» заимствован из геометрии. Прежде чем говорить об условиях подобия физических процессов, вспомним некоторые свойства геометрического подобия. Допустим, что мы имеем два подобных треугольника (рис. 2.12). В подобных треугольниках отношения сходственных сторон равны:
Эти отношения носят название константы подобия 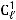

Рис. 2.12 |
Рис. 2.13 |
Константы подобия – это постоянные величины для однородных геометрических (физических) величин, однако при переходе к новым подобным системам числовое значение константы подобия меняется.
Допустим, имеем третий треугольник (рис. 2.13), подобный первым двум. Тогда
Обозначим через 
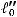
 высоты в треугольниках. Отсюда отношения:
высоты в треугольниках. Отсюда отношения:
- 74 -





 =Idem/Inv.
=Idem/Inv.
Здесь Inv обозначает «одинаковы» (лат.), Idem – «одно и то же» (лат.). Инварианты подобия (Inv) – это относительные геометрические (физические) величины, которые неодинаковы для различных элементов данной системы, но одинаковы для сходственных геометрических (физических) элементов любых подобных систем. Основное свойство
– их неизменность при подобном преобразовании систем. В качестве примера inv геометрического подобия можно привести число 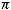 , все тригонометрические функции.
, все тригонометрические функции.
Рассмотренные свойства геометрического подобия могут быть распространены и на физические процессы, при этом различают следующие частные формы физического подобия:
|
1. Подобие кинема- |
|||
|
тическое |
– подобие полей |
||
|
скоростей |
и |
ускорений. |
|
|
Определяется требованием в |
|||
|
геометрически |
сходствен- |
||
|
ных точках, то есть в точках, |
|||
|
подобно |
расположенных, |
||
|
относительные |
значения |
||
|
скоростей |
и ускорений по |
||
|
величине |
и |
направлению |
|
Рис. 2.14 |
должны |
быть |
одинаковы. |
|
При этом |
необходимым |
|||
|
||||
условием кинематического подобия является геометрическое подобие.
На рис. 2.14 |
и |
– значения текущих скоростей в сход- |
ственных точках, |
и |
– значения масштабных скоростей в сход- |
ственных точках. В качестве масштабных значений скоростей может быть выбрана скорость движения во внешнем потоке.
Условие кинематического подобия для двух процессов:
где W – инвариант кинематического подобия.
2. Динамическое подобие – подобие полей, действующих в системах сил. Определяется следующим требованием: в геометрически сходственных точках, то есть в точках, подобно расположенных, относительные значения действующих в системах сил по величине и
- 75 -

направлению должны быть одинаковы. Условие динамического подобия:
где  – масштабное значение давления; P – инвариант динамического подобия.
– масштабное значение давления; P – инвариант динамического подобия.
3. Тепловое подобие полей температур – определяется следу-
ющим требованием: в геометрически сходственных точках относительные значения температур должны быть равны, то есть необходимым условием теплового подобия является геометрическое подобие:
где – новое значение отсчета температуры |
|
|
( – темпера- |
|
|
|
|||
тура жидкости вдали от стенки; |
); |
– масштабное значе- |
||
ние температуры стенки. |
|
|
|
|
Подобие двух физических процессов в данный момент времени означает подобие полей всех относительных величин, характеризующих эти процессы:
Однако это еще не означает, что подобие между двумя процессами будет сохраняться с развитием их во времени. Для того чтобы это подобие сохранялось между физическими процессами с развитием их во времени, необходимо чтобы законы изменения всех относительных величин, характеризующих эти процессы в пространстве и времени, были тождественно одинаковы. Это означает, что дифференциальные уравнения, описывающие подобные процессы, записанные в относительных величинах, должны быть тождественно одинаковы для подобных систем.
- 76 -
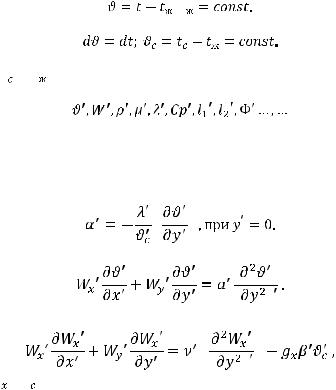
2.3.1. Приведение системы дифференциальных уравнений, описывающих подобные процессы для пограничного слоя к безразмерной форме записи
(метод масштабных преобразований)
Допустим, что мы имеем два подобных стационарных процесса конвективного теплообмена с постоянными физическими свойствами. Пусть это будут процессы теплоотдачи при продольном обтекании поверхности твердого тела безграничным в направлении оси 0Z потоком жидкости, при этом будем считать, что скорость W0 и температура tж во внешнем потоке постоянны.
Выберем новое начало отсчета температуры, в качестве которой возьмем температуру жидкости вдали от стенки:
, 
Заметим, что
Для определенности будем считать, что это процессы нагревания жидкости: 
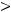

 Обозначим величины, характеризующие первый процесс, одним штрихом ( ' ):
Обозначим величины, характеризующие первый процесс, одним штрихом ( ' ):
Аналогично запишем величины, характеризующие второй процесс, обозначая их двумя штрихами ( '' ).
Запишем исходную систему дифференциальных уравнений для пограничного слоя для первого процесса с учетом принятых нами обозначений. Уравнение теплоотдачи запишется в виде
Уравнение энергии
Уравнение движения


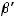
 – объемная подъемная сила, возникающая в жидкости за счет разности температур.
– объемная подъемная сила, возникающая в жидкости за счет разности температур.
- 77 -

Запишем исходную систему дифференциальных уравнений для пограничного слоя для второго процесса, подобно первому, обозначая величины двумя штрихами ( '' ), и потребуем их тождественности.
Выполним запись уравнений теплоотдачи и энергии в относительных величинах. Для этого сформулируем условия теплового, кинематического и геометрического подобия. Дифференциальные уравнения движения в относительных величинах для двух процессов будут записаны без вывода с использованием той же методики. Для записи дифференциальных уравнений теплоотдачи и энергии в относительных величинах необходимо записать условия теплового, геометрического и кинематического подобия. Для этого, в свою очередь, необходимо выбрать масштабы приведения.
В качестве масштабов приведения примем температуру ки 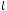 , скорость во внешнем потоке
, скорость во внешнем потоке  , в качестве масштабного линейного размера –
, в качестве масштабного линейного размера – 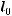 . Тогда условия теплового подобия:
. Тогда условия теплового подобия:
где 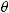 – инвариант теплового подобия. Перепишем эти условия в виде:
– инвариант теплового подобия. Перепишем эти условия в виде:
Текущие значения температур могут быть выражены через их масштабные значения и инвариант теплового подобия.
Условие кинематического подобия
Перепишем в виде
Условие геометрического подобия:
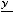

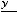

 ,
, 


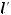
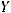 и
и 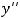

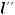





 ,
, 


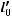
 и
и 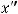

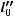

- 78 -

Запишем дифференциальные уравнения теплоотдачи для первого процесса в относительных величинах с учетом принятых нами обозначений:
Дифференциальные уравнения теплоотдачи для первого процесса
(2.10а)
Дифференциальные уравнения теплоотдачи для второго процесса:
(2.10б)
Правые части этих уравнений представляют собой инвариантные производные. Потребуем тождественности дифференциальных уравнений теплоотдачи для первого и второго процессов, записанных в относительных величинах. Для этого должны быть равны левые части уравнений:
где Nu – число Нуссельта. Для раскрытия его физического смысла запишем его в виде
В числителе получим плотность теплового потока в процессе теплоотдачи, передаваемого через слой жидкости у стенки, согласно уравнению Ньютона – Рихмана, в знаменателе – плотность теплового потока, передаваемого через слой жидкости у стенки, согласно уравнению Фурье.
Число Nu определяет соотношение между плотностями тепловых потоков, предаваемых через слой жидкости у стенки путем теплоотдачи и теплопроводности. Число Нуссельта (Nu) характеризует теплоотдачу на границе «стенка – жидкость».
- 79 -

Для двух подобных процессов дифференциальное уравнение теплоотдачи запишется как
(2.11)
Запишем дифференциальное уравнение энергии для первого процесса в относительных величинах. Первое и второе слагаемые:
Аналогично для второго процесса запишем дифференциальное уравнение энергии в относительных величинах для пограничного слоя:
Условия тождественности дифференциальных уравнений энергии в относительных величинах будут соблюдены, если будут тождественно равны:
где Pe – число Пекле.
где 
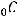
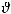 – плотность теплового потока, передаваемого через слой жидкости у стенки путем конвекции;
– плотность теплового потока, передаваемого через слой жидкости у стенки путем конвекции; 
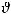 – плотность теплового пото-
– плотность теплового пото-
ка, передаваемая через слой жидкости у стенки путем теплопроводности. На самом деле
Число Pe представляет собой соотношение между плотностями тепловых потоков, передаваемых через слой жидкости у стенки путем конвекции и теплопроводности. В результате дифференциальное
- 80 -

уравнение энергии в относительных величинах для двух подобных процессов запишется:
(2.12)
Условия тождественности дифференциальных уравнений движения для проекции сил на X будут соблюдены, если выполнены определенные условия. Первое условие:
где Re – число Рейнольдса.
где числитель 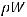
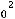 характеризует инерционную силу, а знаменатель
характеризует инерционную силу, а знаменатель 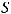


 – силу трения. Число Re определяет соотношение между
– силу трения. Число Re определяет соотношение между
инерционными силами и силами внутреннего трения.
Если в потоке преобладают инерционные силы, а силы трения малы, что может иметь место в центре потока, то в этом случае возможно турбулентное течение жидкости. И, наоборот, если при движении жидкости преобладающими являются силы трения, а инерционные силы малы, что может наблюдаться вблизи у стенки, то в этом случае характер движения будет ламинарным, поэтому число Re – число подобия, определяющее режим движения среды.
Второе условие существования подобия между двумя физическими процессами определяется равенством:
где Gr – число Грасгофа, характеризующее относительную интенсивность подъемной силы, возникающей в жидкости за счет разности плотностей холодных и нагретых частиц жидкости, находящихся в поле действия силы тяжести, по сравнению с действием силы внутреннего трения.
- 81 -
2.3.2. Дифференциальное уравнение движения для двух подобных процессов в относительных величинах
Для решения нашей задачи двух условий тождественности достаточно. Тогда дифференциальное уравнение движения для двух подобных процессов для проекций сил на ось X в относительных величинах без вывода запишется в виде
(2.13)
Заметим, что это уравнение характеризует не только вынужденное, но и свободное движение (число Gr). Однако если в дифференциальном
уравнении движения содержится произведение |
|
|
|
, то необходимо |
|
|
выполнить условие
где Eu – число Эйлера, характеризующее отношение сил давления к инерционным силам. Этих условий достаточно.
Дифференциальное уравнение неразрывности
(2.14)
Таким образом, два подобных процесса описываются одной системой дифференциальных уравнений в относительных величинах.
2.4. Теоремы подобия
Первая теорема подобия. Уравнения, устанавливающие связь между физическими величинами, записанные в относительных величинах, одинаковы для подобных систем. Такая формулировка, свидетельствующая о существовании инвариантов подобия, была сделана еще Ньютоном для случая механического подобия.
В настоящее время первую теорему подобия формулируют так: Подобные между собой физические процессы имеют одинаковые численно равные одноименные числа подобия.
- 82 -
