
Лазеры и волоконная оптика в биомедицинских исследованиях
.pdf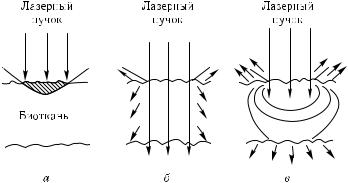
22 |
Гл. 1. Основы лазерной биомедицины |
Т а б л и ц а 1.3. Коэффициенты поглощения, µa, некоторых биотканей, измеренные на отдельных лазерных длинах волн, λ [5, 9, 10, 43–45]
Биоткань |
λ, нм |
µa, см−1 |
Биоткань |
λ, нм |
µa, см−1 |
|
Кровь |
308 |
265 |
Атеросклеротическая |
249 |
650 |
|
Ткань артериаль- |
193 |
10 |
4 |
бляшка в известко- |
308 |
137 ± 33 |
3 |
вом состоянии |
|||||
ной стенки человека |
248 |
10 |
|
351 |
118 ± 17 |
|
(в норме) |
|
|
||||
|
308 |
180 ± 16 |
|
488 |
42 ± 7,9 |
|
|
351 |
145 ± 8,0 |
|
532 |
34 ± 3,7 |
|
|
488 |
32 ± 4,4 |
|
1064 |
7,2 |
|
|
532 |
30 ± 1,8 |
|
2940 |
5000 |
|
|
|
|
|
|
10600 |
500 |
Ткань артериаль- |
308 |
108 ± 17 |
Роговица глаза |
193 |
2700 |
|
ной стенки человека |
351 |
116 ± 11 |
бычков |
248 |
210 |
|
(патология) |
|
|||||
|
488 |
25 ± 3,7 |
|
|
|
|
|
532 |
37 ± 4,5 |
|
|
|
|
интенсивность отраженного биотканью излучения (за счет обратного рассеяния), вплоть до 35–70 % от падающего. Измеренные in vivo значения полного коэффициента отражения (зеркальный и диффузный компоненты) и экспериментальные значения глубины проникновения света для некоторых биотканей на отдельных лазерных и близких им длинах волн представлены в табл. 1.4 и 1.5.
Рис. 1.9. Поглощение и рассеяние лазерного излучения биологическими тканями: а — преобладает поглощение; б — поглощение и рассеяние дают примерно равные вклады; в — преобладает рассеяние [89]
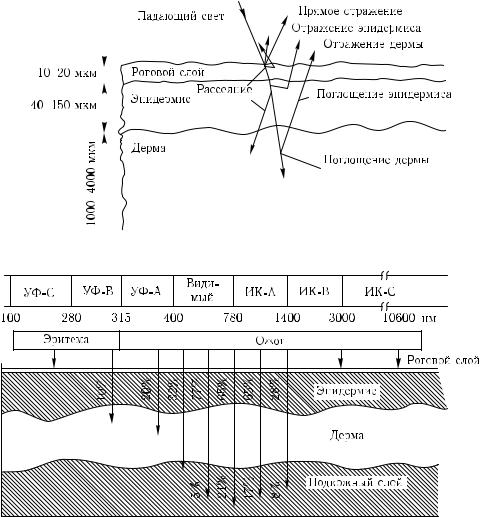
Например, из-за многослойной и многокомпонентной структуры кожи взаимодействие света с ней оказывается весьма сложным [62, 90] (рис. 1.10, 1.11). Роговой слой отражает около 5–7 % падающего излучения. Коллимированный пучок света преобразуется в диффузный из-за микроскопических неоднородностей на границе воздух — роговой слой. Большая часть отраженного кожей света образуется за счет обратного рассеяния различными слоями ткани (роговой слой, эпидермис, дерма и микрососудистая система). Поглощение рассеянного света пигментами кожи дает количественную информацию о концентрации билирубина, насыщении гемоглобина кислородом и содержании лекарственных препаратов в ткани и крови, например
1.4. Рассеяние и поглощение света |
23 |
Т а б л и ц а 1.4. Измеренные in vivo коэффициенты отражения некоторых биотканей, % (френелевский (зеркальный) и диффузный (рассеянный) компоненты [62, c. 114])
Тип ткани |
λ, нм |
Тип ткани |
|
λ, нм |
|
|
|
|
1064 |
|
488/515 |
630 |
|
665 |
1064 |
Кожа руки негра |
44 |
Кожа руки европейца |
– |
– |
|
45 |
44 |
Кожа мыши: |
|
Кролик |
|
|
|
|
|
линия C57 |
29 |
пигментированный: |
|
|
|
|
|
бестимусная |
35 |
мышечная ткань |
11 |
– |
|
19 |
23 |
линия C3H |
24 |
печень |
4 |
– |
|
10 |
30 |
|
|
селезенка |
4 |
– |
|
20 |
26 |
|
|
жировая клетчатка |
18 |
– |
|
30 |
25 |
Мышечная ткань |
|
Меланома пигментная |
|
|
|
|
|
мыши: |
|
(мышь — линия C57) |
5 |
6 |
|
8 |
23 |
линия C57 |
23 |
|
|
|
|
|
|
бестимусная |
23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Печень мыши: |
|
Ретинобластома человека, |
|
|
|
|
|
бестимусная |
41 |
перевитая бестимусной |
|
|
|
|
|
линия C3H |
31 |
мыши: |
|
|
|
|
|
|
|
типичная ткань |
12 |
23 |
|
19 |
17 |
|
|
ткань в геморрагической |
|
|
|
|
|
|
|
области |
7 |
19 |
|
21 |
19 |
|
|
|
|
|
|
|
|
Селезенка |
|
Карцинома молочной |
|
|
|
|
|
бестимусной мыши |
25 |
железы (мышь — линия |
|
|
|
|
|
|
|
C3H) |
9 |
25 |
|
35 |
35 |
|
|
Непигментированная |
|
|
|
|
|
|
|
меланома Грина передней |
|
|
|
|
|
|
|
камеры глаза кролика |
9 |
– |
|
26 |
26 |
Примечание. Типичная относительная ошибка измерений составляет ±0,12.
фотодинамических красителей, что является основой методов диагностики и терапии ряда заболеваний (см. рис. 1.7). Значительное проникновение видимого и ближнего ИК-света через кожу внутрь организма человека, в области длин волн так называемого терапевтического окна (600–1600 нм, см. рис. 1.11), является основой ряда методов фототерапии. Достаточно высокая прозрачность кожи в длинноволновом УФ-свете (УФА), определяемая спектрами поглощения ДНК, триптофана, тирозина, уроканиновой кислоты и меланина (см. рис. 1.8), позволяет осуществлять ряд методов фотохимиотерапии кожи с использованием УФА-излучения [3, 67, 83, 84, 87, 90].
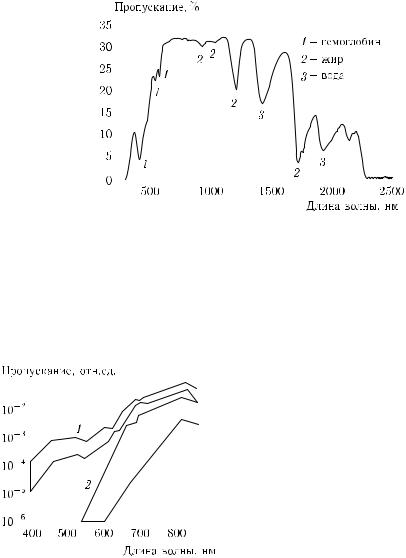
Другим примером гетерогенно многокомпонентной ткани является молочная железа, которая, в основном, состоит из жировой и фиброзной тканей и сосудистой системы. Полосы поглощения гемоглобина крови, жира и воды ясно видны в спектре, измеренном in vitro в слое ткани молочной железы толщиной 3 мм, как показано на рис. 1.12 [209]. Измерение производилось с помощью спектрометра с интегрирующей сферой. Между 700 и 1100 нм имеется широкое окно прозрачности ткани, более узкие окна прозрачности с несколько меньшим пропусканием находятся вблизи длин волн 1300 и 1600 нм.
24 |
Гл. 1. Основы лазерной биомедицины |
|
|
|||
Т а б л и ц а 1.5. Глубина |
проникновения света |
в биоткань (экспериментальные |
значения) |
|||
|
|
|
[9, 43–45, 62] |
|
|
|
|
|
|
|
|
|
|
Тип ткани |
|
λ, нм |
lэ, мм |
Тип ткани |
λ, нм |
lэ, мм |
Ткани руки |
|
600 |
1,4 |
Стенка мочевого пузыря |
633 |
1,9 |
человека (in vivo) |
|
650 |
2,0 |
|
1064 |
5,2 |
|
|
|
|
|
|
|
|
|
700 |
2,6 |
Эпителиальная карцинома |
633 |
2,2–2,3 |
|
|
750 |
2,7 |
мочевого пузыря |
1064 |
5,2 |
|
|
800 |
3,0 |
|
|
|
|
|
850 |
3,0 |
Слизистая оболочка |
633 |
1,1 |
|
|
900 |
3,0 |
бронхов |
|
|
|
|
|
|
|
|
|
Ткани человека (посмертно) |
|
|
|
Спавшаяся ткань легких |
633 |
0,9 |
|
|
|
|
|
|
|
Белое вещество |
|
515 |
0,4–0,6 |
Чешуйчатая карцинома |
|
|
мозга подростка |
|
660 |
1,2–1,6 |
легких |
633 |
1,6 |
|
|
1064 |
3,2–4,3 |
|
|
|
|
|
|
|
|
|
|
Мозг |
|
515 |
1,1–1,7 |
Стенка аорты: |
|
|
новорожденного |
|
660 |
3,7–5,4 |
частично |
515 |
0,2–0,4 |
|
|
1064 |
7,1–8,8 |
обызвествленная |
633 |
0,7–1,0 |
Астроцитома |
|
515 |
0,5–1,3 |
в области некротичес- |
|
|
|
|
660 |
2,0–3,0 |
кой язвы |
633 |
0,4 |
|
|
1064 |
3,0–6,3 |
в норме при ненарушен- |
515 |
0,4 |
|
|
|
|
|
|
|
Полиморфная |
|
515 |
1,4 |
ном кровоснабжении |
633 |
1,1 |
глиобластома |
|
1064 |
6,6 |
|
|
|
Овсяно-клеточные |
|
515 |
0,6 |
Жировая ткань, |
515 |
0,7 |
метастазы рака легких |
|
660 |
1,3 |
прилегающая к аорте |
633 |
1,8 |
в мозге |
|
1064 |
2,8 |
|
|
|
|
|
|
|
Измерения in vitro |
|
|
|
|
|
|
|
|
|
Опухолевые ткани мыши |
|
|
|
Ретинобластома челове- |
600 |
2,9 |
(измерения in vivo с помощью |
|
ка, перевитая бестимусной |
650 |
3,8 |
||
изотропного волоконного датчика) |
|
мыше |
700 |
4,0 |
||
|
|
|
|
|
|
|
Ретинобластома |
|
488/ |
|
|
750 |
4,0 |
бестимусной |
|
515 |
1,6 |
|
800 |
4,1 |
мыши |
|
630 |
3,3 |
|
850 |
4,2 |
|
|
665 |
3,6 |
|
900 |
4,3 |
|
|
1064 |
7,5 |
|
1064 |
5,1 |
Карцинома |
|
488/ |
|
Ткани быка (измерения |
|
|
молочной железы |
|
515 |
1,1 |
с помощью волоконного |
|
|
(линия C3H) |
|
630 |
2,0 |
датчика) |
|
|
|
|
665 |
2,3 |
Мышечная ткань |
633 |
2,6 ± 0,5 |
|
|
1064 |
3,7 |
|
1064 |
4,3 ± 0,9 |
|
|
|
|
|
|
|
B16 пигменти- |
|
630 |
0,5 |
Печень |
633 |
1,5 ± 0,1 |
рованная |
|
665 |
0,5 |
|
1064 |
3,1 ± 0,5 |
|
|
|
|
|
|
|
меланома (линия C57) |
|
1064 |
2,0 |
Мозг теленка |
633 |
2,9 ± 0,7 |
|
|
|
|
|
1064 |
4,0 ± 0,8 |
B16 пигменти- |
|
650 |
0,28 |
Мозг свиньи |
600 |
1,8 |
рованная |
|
700 |
0,34 |
|
650 |
2,4 |
меланома |
|
750 |
0,41 |
|
700 |
2,9 |
бестимусной |
|
800 |
0,50 |
|
750 |
3,0 |
мыши |
|
850 |
0,56 |
|
800 |
3,3 |
|
|
900 |
0,64 |
|
850 |
3,5 |
|
|
1064 |
1,4 |
|
900 |
3,7 |
|
|
|
|
|
1064 |
4,0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.4. Рассеяние и поглощение света |
25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1.10. Взаимодействие света с кожей [90]
Рис. 1.11. Пропускание света различных длин волн кожей [62]
Твердые ткани, такие как ребра и черепная коробка, и цельная кровь также демонстрируют сравнительно хорошее пропускание в видимой и ближней ИК-облас- ти спектра [3, 46, 69, 187] (рис. 1.13–1.15).
При анализе распространения света в биотканях с многократным рассеянием предполагают обычно равномерное распределение поглощающих и рассеивающих центров. Для УФА, видимого и ближнего ИК-излучения типичным является анизотропное рассеяние, которое характеризуется сильной направленностью однократно рассеянных фотонов, что связано с присутствием больших клеточных органелл, таких как митохондрии, лизосомы, внутренние мембраны (аппарат Гольджи) [3, 13, 30–32, 201, 202]. Сильная анизотропия рассеяния биотканей и многократный его характер приводят к отклонению характера пропускания света от закона Бугера–Бера (см. уравнение (1.1)).
26 |
|
|
Гл. 1. Основы лазерной биомедицины |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1.12. Спектр пропускания 3-мм слоя биоткани молочной железы. Использовался спектрометр с интегрирующей сферой. Отмечены вклады полос поглощения компонентов биоткани: 1, гемоглобин; 2, жир; 3, вода [209]
Кроме того, для многих тканей, таких как, например, кожа, сетчатка глаза, кровь, характерна и неоднородность поглощения. Известно, что значение коэффициента поглощения меланиновых гранул сетчатки глаза в 10 раз больше, чем окружающей ткани, а распределение их неравномерное. Неравномерно распределен также гемоглобин, сильно поглощающий свет в синей области (см. рис. 1.7), в суспензии нативных
эритроцитов. При неравномерном распределе-
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нии молекул хромофоров в среде проявляет- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ся так называемый эффект сита и измеряе- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
мая оптическая плотность занижается [83]. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Это занижение тем больше, чем выше опти- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ческая плотность поглотителей. В результате |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
как рассеяние света, так и эффект сита при- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
водят к сглаживанию спектров ослабления по |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сравнению со спектрами поглощения молекул |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
хромофоров. В максимумах спектров ослаб- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ления, где эффект сита оказывается сильнее, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
оптическая плотность занижается, а в ми- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нимумах, где проявляется влияние рассеяния |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
света, эта величина завышается. |
|
Рис. 1.13. Спектры пропускания: 1 — |
Многократное рассеяние и поглощение от- |
||||||||||||||||||
вечают за уширение лазерного пучка и его |
|||||||||||||||||||
стенка грудной клетки в области ребра |
ослабление по мере распространения в ткани, |
||||||||||||||||||
(толщина 16–20 мм, 5 человек); 2 — |
|||||||||||||||||||
в то время как объемное рассеяние является |
|||||||||||||||||||
черепная коробка с кожным покровом |
|||||||||||||||||||
(толщина 2–13 мм, 3 трупа) [46] |
основной причиной возникновения значитель- |
|
ной дисперсной составляющей излучения в |
||
|
||
|
обратном направлении. Таким образом, рас- |
пространение света в ткани зависит от рассеивающих и поглощающих свойств ее компонентов: клеток, клеточных органелл и разнообразных волокнистых структур [1–3, 31, 48, 211–214]. Размеры, форма и плотность этих структур, их показатель преломления по отношению к окружающему веществу, поляризационное состояние падающего света — все это играет важную роль в распространении света через ткани [1–3, 13, 30–32].
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.4. Рассеяние и поглощение света |
27 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
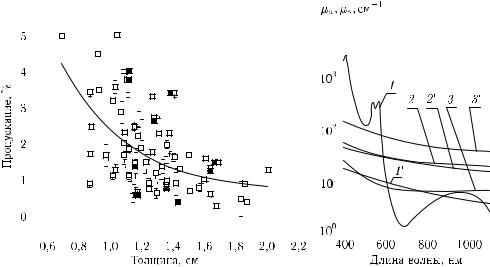
Рис. 1.14. Зависимость пропускания черепной коробки |
Рис. 1.15. |
Спектральные за- |
человека с кожным покровом (20 трупов, 5 областей: лоб- |
висимости для коэффициентов |
|
ная часть, левая и правая височная части, затылочная и |
поглощения |
(µa) и рассеяния |
теменная части, всего 100 экспериментальных точек) для |
(µs) крови (1, 1′), эпидермиса |
|
коллимированного излучения диодного лазера на длине |
(2, 2′) и дермы (3, 3′) [69] |
|
волны 810 нм (мощность 1 Вт, диаметр расширенного пучка 30 мм) от ее толщины [187]
Ввиду огромного разнообразия и структурной сложности тканей разработка адекватных оптических моделей, учитывающих рассеяние и поглощение света, часто представляет собой наиболее сложную часть исследования. Два подхода обычно используются для моделирования тканей. В первом из них ткань моделируется средой со случайным непрерывным распределением оптических параметров в пространстве, а во втором ткань рассматривается как дискретный ансамбль рассеивателей [1–3, 13, 30–32]. Выбор подхода диктуется как структурной спецификой изучаемой ткани, так и типом искомых характеристик светорассеяния.
Большинство тканей состоит из структур, размеры которых варьируют в широком диапазоне, что чаще всего можно описать как случайный континуум неоднородностей показателя преломления с переменным пространственным масштабом. В частности, с помощью фазоконтрастной микроскопии было показано, что структура неоднородностей показателя преломления в тканях млекопитающих во многих случаях аналогична структуре замороженной турбулентности [215, 216]. Этот факт имеет фундаментальное значение для понимания особенностей распространения света в ткани и может послужить ключом к решению обратной задачи реконструкции структуры ткани. Данный подход применим к тканям, не имеющим выраженных границ между элементами, обладающими значительной неоднородностью. Процесс рассеяния в таких структурах при определенных условиях может быть описан с использованием модели фазового экрана.
Второй подход к моделированию тканей состоит в их представлении системой дискретных рассеивающих частиц. В частности, эта модель успешно использовалась для описания угловой зависимости поляризационных характеристик рассеянного
28 |
Гл. 1. Основы лазерной биомедицины |
излучения. Кровь является наиболее важным биологическим примером дисперсной системы, полностью соответствующей модели дискретных частиц.
Биологические среды часто моделируются ансамблем однородных сферических частиц, поскольку многие клетки и микроорганизмы, в частности клетки крови, по форме близки к сферам или эллипсоидам. Система невзаимодействующих сферических частиц является простейшей моделью ткани. Дифракция света на сферической частице строго описывается теорией Ми [217, 218]. Развитие этой модели включает учет структуры сферических частиц, а именно многослойные сферы и сферы с радиальной неоднородностью, анизотропией и оптической активностью [219, 220].
Поскольку соединительные ткани состоят из волокнистых структур, наиболее подходящей моделью для них является система длинных цилиндров. Мышечная ткань, дерма кожи, твердая мозговая оболочка (dura mater), роговица глаза и склера принадлежат к этому типу тканей, образованному преимущественно коллагеновыми волокнами. Решение задачи дифракции света на одном однородном или многослойном цилиндре также хорошо известно [217].
Для некоторых тканей распределение рассеивающих частиц по размерам может быть существенно монодисперсным, а для других — напротив, весьма широким. Примерами двух таких противоположных случаев являются прозрачная строма роговицы глаза, имеющая острое монодисперсное распределение, и мутная склера глаза, имеющая весьма широкое распределение коллагеновых волокон по диаметрам [13, 31]. Не существует универсальной функции распределения частиц по размерам, которая могла бы описать все ткани с одинаковой степенью адекватности. В оптике дисперсных систем типичными являются гауссово, гамма и степенное распределения [221]. Полидисперсность для случайно распределенных рассеивателей может быть учтена путем использования гамма-распределения, либо асимметричного логарифмического распределения по диаметрам, сечениям или объемам [13, 31, 215, 216, 222, 223]. В частности, для сильно рассеивающих тканей, таких как склера глаза, применимо гамма-распределение по радиусам [222, 223].
1.5. Простейшие дискретные модели ткани
Простейшая модель биологической ткани, дающая приемлемое количественное описание оптических свойств в достаточно широком диапазоне длин волн, может быть представлена в виде монодисперсной системы невзаимодействующих дискретных частиц [225, 226]. Поскольку основными компонентами биоткани являются сравнительно крупные частицы, то рассеяние и поглощение света этими частицами рассчитываются по теории Ми, справедливой для отдельной сферической частицы. При этом радиус частицы a и ее комплексный показатель преломления,
ns(λ0) = ns′(λ0) + ins′′(λ0), |
(1.2) |
показатель преломления основной среды, в которую погружены частицы, n0(λ0), и относительный показатель преломления вещества рассеивающих частиц и основного материала, m = ns/n0, являются параметрами, которые нужно задавать при моделировании. Здесь λ0 — длина волны света в вакууме. Мнимая часть комплексного показателя преломления материала характеризует потери из-за поглощения.
Врамках теории Ми выражения для сечений рассеяния σsca и поглощения σabs,
атакже среднего косинуса угла рассеяния ϑ, так называемого фактора анизотропии

1.5. Простейшие дискретные модели ткани |
29 |
рассеяния g = hcos ϑi, для одной частицы можно записать в виде [217]:
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
λ02 |
|
X∞ |
|
|
2 |
2 |
|
|
|
|
|
|
|
σsca = |
|
|
(2n + 1)(|an| |
|
+ |bn| ), |
|
|
|
|
|
|
|||
2πn02 |
|
|
|
|
|
|
|
|||||||
|
|
|
n=1 |
|
|
|
|
|
|
|
|
|
|
|
|
λ02 |
|
X |
|
|
|
|
2 |
2 |
|
|
|
|
|
σabs = |
|
|
(2n + 1)[Re(an + bn) − (|an| |
+ |bn| )], |
|
|
|
|||||||
2πn02 |
|
|
|
|||||||||||
|
|
|
n=1 |
2n + 1 |
|
|
∞ |
n(n + 2) |
|
|
|
|
||
|
λ02 |
∞ |
|
|
|
|||||||||
g = |
|
|
|
X |
|
|
Re(a b ) + |
X |
|
Re(a a |
n+1 |
+ b b |
) , |
|
2 |
|
|
|
|
|
|
|
|||||||
|
|
|
(n=1 n(n + 1) |
|
n n |
|
n + 1 |
n |
n n+1 |
) |
||||
|
πn0 |
σsca |
|
|
n=1 |
|
|
|
||||||
(1.3)
(1.4)
(1.5)
где an и bn — коэффициенты Ми, являющиеся функциями относительного комплексного показателя преломления частиц (m) и параметра 2πan0/λ0; звездочка обозначает комплексное сопряжение:
an =
bn =
ψn(α)ψn′ (mα) − mψn (mα)ψn′ (α) , ξ(α)ψn′ (mα) − mψn(mα)ξn′ (α)
mψ′(mα)ψn(α) − ψn(mα)ψn′ (α) , mψn′ (mα)ξn (α) − ψn(mα)ξn′ (α)
α = 2πan0 , λ0
(1.6)
(1.7)
(1.8)
где ψn, ξn, ψn′ , ξn′ — функции Риккати–Бесселя первого и второго рода. Коэффициенты поглощения µa и рассеяния µs для ансамбля невзаимодействую-
щих частиц вычисляются с учетом плотности частиц в ткани:
µs = ρσsca, µa = ρσabs, |
(1.9) |
где ρ — плотность рассеивающих частиц.
Среднее сечение рассеяния на одну частицу можно представить в виде, удобном для экспериментальных оценок [217]:
|
λ2 |
|
|
π |
|
σsca = |
|
1 |
I(ϑ) sin ϑ dϑ, |
(1.10) |
|
|
|
||||
|
2π I0 |
|
|||
|
0 |
|
|||
где I0 — интенсивность падающего света, I(ϑ) — угловое распределение света, рассеянного частицей, ϑ — угол рассеяния. Для макроскопически изотропных и однородных сред среднее сечение рассеяния не зависит от направления и поляризации падающего света. Средние сечения экстинкции, σext = σsca + σabs, и поглощения, σabs, также не зависят от направления и состояния поляризации падающего света.
В свою очередь, фактор анизотропии рассеяния g определяется видом фазовой (или угловой) функции рассеяния p(ϑ):
π |
|
|
g ≡ hcos ϑi = |
p(ϑ) cos ϑ · 2π sin ϑ dϑ. |
(1.11) |
0 |
|
|
Фазовая функция рассеяния p(ϑ) |
характеризует элементарный |
акт рассеяния |
в среде, будучи функцией плотности вероятности рассеяния света в определенном направлении, отличном от направления падающей на частицу волны. Фазовая функция зависит только от угла рассеяния ϑ (угол между направлениями) в том случае, если рассеяние симметрично относительно направления падающей волны.

30 |
Гл. 1. Основы лазерной биомедицины |
Введение удельных коэффициентов рассеяния и поглощения, экстраполированных к объемной доле 100 %, полезно для описания рассеивающих и поглощающих свойств моделируемой среды. В этом случае, при условии, что частицы достаточно удалены друг от друга чтобы предотвратить зависимое рассеяние, коэффициент рассеяния µs, приведенный (транспортный) коэффициент рассеяния µ′s = (1 − g)µs и коэффициент поглощения µa пропорциональны объемной доле рассеивающих частиц cs:
|
µs = csσbsca, |
|
|
|
|
|||
|
µs′ = csσbsca[1 − g(λ0, a)], |
|
|
(1.12) |
||||
|
µa = csσbabs, |
|
|
выражены в см−1. |
||||
где удельные коэффициенты рассеяния и поглощения σsca |
и σabs |
|||||||
Среднее расстояние |
между центрами тяжести частиц определяется их радиусом |
|
||||||
и объемной долей cs:ds |
|
2a |
b |
b |
|
a |
||
|
ds = |
√3 |
|
. |
|
|
(1.13) |
|
|
cs |
|
|
|||||
Теория Ми строго применима только к частицам определенной правильной формы, но ее результаты полезны и в случае частиц неправильной формы. При этом колебания коэффициента рассеяния и фактора анизотропии при изменении размера частиц, наблюдаемые для сферических частиц (см. рис. 1.16), усредняются [217]. Удельный транспортный коэффициент рассеяния µ′s/cs существенно увеличивается с ростом относительного показателя преломления n′s/n0. В свою очередь, фактор анизотропии рассеяния g максимален и стремится к единице, а µ′s/cs = 0, когда указанное отношение равно 1 (рис. 1.16).
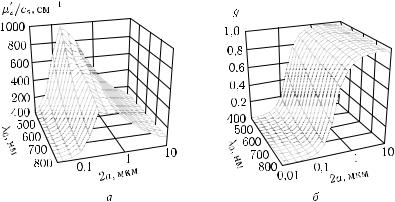
Рис. 1.16. Рассеивающие свойства непоглощающих частиц на длине волны He–Ne-лазера (633 нм), рассчитанные с использованием теории Ми [225, 226]. Удельный транспортный коэффициент рассеяния µ′s/cs (а) сильно зависит как от размера частиц (2a), так и от их относительного показателя преломления (n′s/n0). При условии, что показатели преломления рассеивателей и окружения согласованы (n′s/n0 = 1), коэффициент рассеяния равен нулю, а фактор анизотропии рассеяния максимален и стремится к 1 (б). Быстрые осцилляции на
графиках связаны с наличием резонансов Ми
Зависимости параметров рассеяния частиц с показателем преломления, близким к показателю преломления окружающей среды, n′s/n0 = 1,07, что характерно для многих биологических тканей и крови, от длины волны показаны на рис. 1.17. При расчетах пренебрегали дисперсией материала частиц и окружающей среды, однако на практике она может быть важна. Из этих расчетов следует, что коэффициент рассеяния системы частиц с диаметром, меньшим длины волны, убывает
1.5. Простейшие дискретные модели ткани |
31 |
с ростом длины волны, в то время как при диаметре частиц, большем длины волны, он почти постоянен (рис. 1.17, а). Фактор анизотропии рассеяния g менее зависим от длины волны. Имеются плато в зависимостях при размерах частиц много меньше (изотропное рассеяние, g ≈ 0) и много больше (сильно анизотропное рассеяние g 6 1), чем длина волны, между которыми расположен участок крутого возрастания (рис. 1.17, б).
Рис. 1.17. Зависимости параметров рассеяния непоглощающих частиц от длины волны при n′s/n0 = 1,07, рассчитанные с использованием теории Ми [225, 226]. Удельный транспортный коэффициент рассеяния µ′s/cs (а) для частиц с размерами, меньшими длины волны, сильно растет в сторону коротких длин волны. Частицы с диаметром больше длины волны имеют почти постоянный удельный транспортный коэффициент рассеяния по всему видимому диапазону. Фактор анизотропии рассеяния g (б) почти не зависит от длины волны, но сильно
зависит от размера частиц
Представленная модель показывает, что для адекватного описания оптических свойств биологической ткани нужно знать размеры и показатели преломления ее структурных элементов. Учет распределения частиц по размерам и показателям преломления, а также взаимодействия между частицами при их плотной упаковке существенно улучшает модель.
Показатель преломления биоткани может быть рассчитан с использованием закона Глэдстоуна и Дейла, из которого следует, что для многокомпонентной среды при отсутствии химического взаимодействия между компонентами, ее показатель преломления является средним от показателей преломления компонентов с их объемными долями в качестве весовых множителей, т. е. [227]
N |
X |
|
X |
|
|
n = nifi, |
fi = 1, |
(1.14) |
i=1 |
i |
|
где ni и fi — показатель преломления и объемная доля отдельных компонентов клетки или ткани соответственно, а N — число компонентов.
Средний показатель преломления основного вещества ткани определяется как взвешенное среднее показателей преломления цитоплазмы клеток, составляющих
ткань, ncp, и интерстициальной жидкости, окружающей клетки и волокнистые струк- |
|
туры ткани, nis, как |
|
n0 = fcpncp + (1 − fcp)nis, |
(1.15) |
